3.1 Основне лінеаризоване рівняння і його розв’язок

У попередніх розділах розв’язано декілька окремих задач стійкості прямих стрижнів. У цьому розділі дано виведення загального лінеаризованого рівняння для довільно навантаженого пружного прямого стрижня змінного поперечного перетину, сформульовані граничні умови і наведені приклади точного і наближеного розв’язку цього рівняння.

Розглянемо стрижень у системі прямокутних координат, як показано на рис. 3.1 а, причому візьмемо, що одна з головних центральних осей поперечного перетину стрижня лежить у площині .

Лінеаризоване рівняння вигину стрижня в площині отримаємо за таких припущень.

1. Вісь ненавантаженого стрижня ідеально пряма і всі зовнішні навантаження і реакції опор до втрати стійкості діють строго уздовж цієї осі.

2. Зовнішні навантаження «мертві», тобто при деформаціях стрижня вони не змінюються ні за величиною, ні за напрямком.

3. Зміна геометричних розмірів стрижня при докритичних деформаціях вважається настільки малою, що нею можна знехтувати; зокрема, у процесі навантаження довжина стрижня, площа і момент інерції його поперечного перетину вважаються незмінними.

4. Зв'язок між внутрішнім згинальним моментом і поперечним прогином стрижня при втраті стійкості описується звичайною залежністю лінійної теорії вигину балок, що базується на гіпотезі плоских перетинів.

a)

б) в)

Рисунок 3.1

Через перше припущення можлива прямолінійна початкова форма рівноваги навантаженого стрижня. При достатньо малих навантаженнях прямолінійна форма рівноваги є єдиною і стійкою. Визначимо умови, за яких можливі форми рівноваги стрижня з зігнутою віссю, суміжні з початковою прямолінійною формою.

Умова рівноваги елемента невикривленого стрижня (рис. 3.1 б) приводить до рівняння

(3.1)

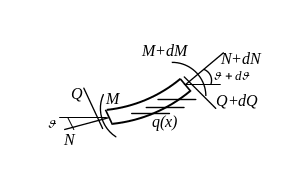
Надалі вважатимемо відомим закон зміни початкових осьових зусиль по довжині стрижня . Розглянемо рівновагу елемента стрижня у викривленому, відхиленому від початкового стані (рис. 3.1 в), причому поперечні прогини вважатимемо нескінченно малими. Оскільки порядок малості достатньо гладкої функції зберігається при диференціюванні, тому і т.д. можна вважати величинами першого порядку малості (оскільки якщо , то ). В усіх остаточних залежностях відповідно до основної ідеї лінеаризації (див. п. 1.5) слід залишати тільки величини першого порядку малості. Зокрема, при складанні рівнянь рівноваги викривленого елемента необхідно взяти, що

Тоді, проектуючи на вісь усі сили, що діють на викривлений елемент, отримаємо

як величину вищого порядку малості не враховуємо і приходимо до рівняння

(3.2)

Прирівнявши до нуля суму проекцій всіх сил на вісь і суму всіх моментів, а також виключивши величини вищих порядків малості, отримаємо ще два рівняння:

(3.3)

Враховуючи четверте припущення і останнє рівняння, внутрішній момент, що вигинає і внутрішня поперечна сила пов'язані з прогинанням такими самими залежностями, як і при звичайному поперечному вигині , де - згинальна жорсткість стрижня в площині .

Доданок слід виключити з рівняння (3.2) як величину другого порядку малості. Тоді це рівняння не відрізнятиметься від рівняння рівноваги невикривленого елемента стрижня (3.1). Отже, при нескінченно малих поперечних прогинах початкове осьове зусилля залишається незмінним з точністю до величин другого порядку малості. Враховуючи сказане, в першому рівнянні (3.3) можна припустити, що Оскільки та , остаточно отримаємо

(3.4)

Це лінійне однорідне рівняння четвертого порядку є основним рівнянням теорії стійкості прямих пружних стрижнів. Воно використовується при будь-яких законах зміни жорсткості , при будь-яких навантаженнях і умовах закріплення, що задовольняють сформульовані вище припущення. Для однопролітного стрижня відповідно до порядку рівняння (3.4) повинні бути сформульовані чотири граничні умови (по два на кожному з кінців). Через перше припущення ці умови мають бути однорідними. Якщо всі зовнішні навантаження вважати такими, що змінюються пропорційно одному параметру , то рівняння (3.4) можна переписати у такому вигляді:

(3.4 а)

де - закон зміни початкових внутрішніх зусиль в невикривленому стрижні при Таким чином, визначення умов існування викривлених форм рівноваги первинно прямолінійного стрижня звелося до розв’язання задачі на власні значення. Для того щоб знайти умови існування викривлених форм рівноваги, суміжних із початковою прямолінійною формою, необхідно знайти значення параметра навантаження , при яких однорідне рівняння (3.4 а) за однорідних граничних умов має нетривіальний розв’язок.

Розглянемо можливі граничні умови в задачах стійкості прямих стрижнів. Геометричні граничні умови формулюються так само, як і в задачах поперечного вигину балок: на кінці стрижня можуть бути відсутні поперечне переміщення (шарнірне опирання), кут повороту (затиснення) або і те й інше одночасно. Силові граничні умови для ненавантаженого кінця аналогічні силовим граничним умовам задач поперечного вигину. Якщо поперечні переміщення на кінці не обмежені, то поперечна сила дорівнює нулю, тобто . Коли кути повороту не обмежені, то згинальний момент дорівнює нулю, тобто . На вільному кінці і поперечна сила, і згинальний момент дорівнюють нулю.

а) б)

Рисунок 3.2

Принципова відмінність силових граничних умов задач стійкості від силових граничних умов лінійних задач поперечного вигину виявляється тоді, коли на один із кінців стрижня прикладаються зосереджені зовнішні зусилля. Це обумовлене тим, що, як вже було зазначено вище, в задачах стійкості розглядаються умови рівноваги у відхиленому, викривленому положенні системи. Тому якщо, наприклад, до вільного кінця стрижня прикладена осьова сила , та умова рівноваги елемента (рис 3.2 б), що примикає до кінця, складена для його відхиленого положення (у проекції на вісь ), приводить до рівняння У даному випадку , тобто отримуємо таку граничну умову при .

При формулюванні силових граничних умов на особливу увагу заслуговують ті випадки, коли зовнішні навантаження передаються на стрижень за допомогою проміжних деталей, що змінюють при вигині стрижня силову дію, що сприймається ним. Декілька прикладів такого навантаження стрижнів наведено на рис. 3.3, де для кожного випадку вказані відповідні граничні умови.

a)

б)

в)

Рисунок 3.3

Так, наприклад, на правий кінець стрижня, зображеного на рис. 3.3 а, передається згинальний момент, що пропорційний довжині жорсткого важеля і кута повороту дотичної до осі стрижня над правою опорою. Звідси випливає гранична умова тобто при . При вигині консольного стрижня, що навантажується через жорсткий шатун (рис. 3.3 б), на правий його кінець, окрім поздовжньої сили , передається поперечна сила, пропорційна куту нахилу жорсткого важеля . У цьому випадку, враховуючи міркування, що були зроблені при визначенні граничних умов для стрижня на рис. 3.2, отримуємо при . Аналогічно поперечна сила (але протилежного знака) виникає при вигині, показаного на рис. 3.3 в стрижня, що навантажується за допомогою гнучкої нитки.

Точний розв’язок рівняння (3.4) можна знайти не завжди. Розглянемо приклади, коли його можна отримати в аналітичному вигляді. Наприклад, якщо стрижень постійної жорсткості стислий однією поздовжньою силою , то , і рівняння (3.4) набуває вигляду

(3.5)

Це рівняння з постійними коефіцієнтами допускає точний розв’язок за будь-яких граничних умов. Перепишемо рівняння (3.5) у вигляді

(3.6)

Підставляючи розв’язок рівняння (3.6) у вигляді , отримаємо

(3.7)

де - довільні постійні.

Як зазначалося вище, для однопролітного стрижня повинні бути задані чотири граничні умови. Підставивши в них загальний розв’язок (3.7), отримаємо систему чотирьох однорідних лінійних рівнянь стосовно чотирьох невідомих . Прирівнюючи до нуля визначник цієї системи, можна знайти власні значення задачі і відповідні їм власні функції. Найменше з власних значень дає критичне значення навантаження, а відповідна йому власна функція описує форму зігнутої осі стрижня при втраті стійкості. Викладену схему розв’язання використаємо, наприклад, для визначення критичної сили і форми зігнутої осі при втраті стійкості стрижня, зображеного на рис. 3.4.

а) б)

Рисунок 3.4

Оскільки жорсткість стрижня є постійною по всій довжині, то граничними умовами цієї задачі є такі:

Використовуючи ці граничні умови для рівняння (3.7), приходимо до системи лінійних однорідних рівнянь

(3.8)

Характеристичне рівняння, з якого визначаються власні значення задачі, можна знайти, прирівнявши до нуля визначник отриманої системи. При аналітичному розв’язанні значно зручніше не розкривати визначників високого порядку, а, послідовно виключаючи невідомі з початкової системи рівнянь, виразити постійні через яку – небудь одну з них, що не дорівнює нулю. У даному прикладі згідно з першими двома рівняннями системи (3.8) З третього рівняння випливає, що Підставивши це значення в останнє рівняння, отримаємо Необхідна умова існування розв’язків, що не дорівнюють тривіальному (рівність нулю виразу, що стоїть у дужках), приводить до характеристичного рівняння Розв’язавши це трансцендентне рівняння, знайдемо власні значення задачі (графічний розв’язок даного рівняння наведено на рис. 3.4 б):

Оскільки у даному прикладі то власні функції виражаються наступними залежностями, отриманими із загального розв’язку (3.7) при підстановці відповідних власних значень :

Найменше (перше) власне значення дає критичне значення стискаючої сили

Власна функція, що відповідає першому власному значенню, з точністю до масштабу описує форму зігнутої осі стрижня при втраті стійкості (рис. 3.4 а):

Для даної конкретної задачі, як і взагалі для задач стійкості, безпосередній практичний інтерес являє тільки перше власне значення, що дає значення критичної сили, і перша власна функція, що описує форму втрати стійкості. Решта власних функцій може бути корисна для побудови наближених розв’язків складніших задач з тими самими граничними умовами.

Аналогічно може бути розв’язана і будь-яка інша задача стійкості рівномірно стислого стрижня з постійною згинальною жорсткістю. Причому кінцевий вираз критичної сили, як правило, записується в одному з двох варіантів (див. формулу 1.1):

Окрім наведених простих прикладів, є велика кількість інших складніших задач, що допускають точне аналітичне розв’язання. Проте у загальному випадку при довільних законах зміни та рівняння (3.4) не вдається аналітично проінтегрувати (це стосується і випадків, коли діє розподілена сила). Тоді для визначення критичних навантажень і форм зігнутої осі стрижня при втраті стійкості використовують наближені методи. Одним із найбільш ефективних машинних методів визначення критичних навантажень у задачах стійкості прямих стрижнів є метод початкових параметрів. Перш ніж перейти до викладення прикладів використання цього методу, необхідно підкреслити, що не завжди доцільно застосовувати повне рівняння четвертого порядку (3.4). У ряді випадків вдається заздалегідь знизити порядок цього рівняння й істотно спростити розв’язок (і аналітичний, і особливо чисельний). Зупинимося зараз на двох основних випадках пониження порядку рівняння (3.4).

Для шарнірно опертого стрижня (рис. 3.5 а), стиснутого осьовою силою , початкове внутрішнє зусилля У цьому випадку, двічі проінтегрувавши рівняння (3.4), отримаємо

.

Рисунок 3.5

Граничні умови:

З двох перших граничних умов знаходимо . З останніх двох граничних умов отримуємо . Тобто приходимо до рівняння другого порядку

. (3.9)

Розв’язок цього рівняння має вигляд . З першої та третьої граничних умов отримуємо Розв’язання відповідає тривіальному розв’язку задачі, тобто невикривленому стану рівноваги стрижня. З умови отримуємо . Найменше власне значення дає таке критичне значення стискаючої сили , а відповідна власна форма (одна півхвиля синусоїди).

Для стрижня, показаного на рис. 3.5 б, граничні умови мають вигляд

З цих граничних умов отримуємо таку систему для визначення постійних :

звідки

Умовою отримання нетривіального розв’язку цієї задачі є

.

Розкриваючи визначник, отримаємо

,

або, зробивши відповідні тригонометричні перетворення,

.

Розглянемо першу умову

,

звідки

або

Відповідне найменше значення навантаження дорівнює

З другої умови , використовуючи розв’язок для стрижня на рис. 3.4, отримуємо , що є більшим за знайдене з першої умови значення ( ). Тобто для стрижня (рис. 3.5 б) критичним навантаженням є

Читачам пропонується самим визначити критичне навантаження і відповідну форму для стрижня, наведеного на рис. 3.5 в.

Рівняння (3.9) можна вивести і з умови рівноваги частини стрижня у відхиленому положенні (див. п.1.2). Неважко переконатися, що рівняння (3.9) справедливе при розв’язанні задач стійкості стрижнів, також зображених на рис. 3.5 б (так зване ковзаюче затиснення) і в (один кінець затиснений - інший вільний). Вони еквівалентні задачі стійкості шарнірно опертого стрижня зі згинальною жорсткістю , що симетрично змінюється щодо середнього перетину.

Іноді для пониження порядку основного рівняння як шукану невідому доцільно розглядати не поперечний прогин, а кут повороту . Тоді, замінивши в рівнянні (3.4) на і проінтегрувавши один раз, отримаємо . Якщо на одному з кінців стрижня (наприклад, при ) поперечні зсуви не обмежені, то однією з граничних умов буде Отже, у цьому випадку і можна записати

(3.10)

Для деяких практично важливих випадків це рівняння другого порядку допускає точне розв’язання.

Так, наприклад [1], для стрижня постійного поперечного перетину, що перебуває під дією власної ваги, враховуючи, що в цьому випадку та (рис. 3.6), і використовуючи підстановку

рівняння (3.10) можна привести до канонічного вигляду рівняння Бесселя

Рисунок 3.6

Розв’язання цього рівняння добре вивчене і зводиться до табульованих функцій Бесселя. Зокрема, підпорядковувавши розв’язок рівняння Бесселя граничним умовам і , можна знайти, що