2.5 Метод Гальоркіна

Метод Гальоркіна заснований на властивості ортогональних функцій. З курсу математичного аналізу відомо, що якщо є сімейство безперервних функцій

і інтеграл добутку будь-яких двох різних функцій цього сімейства в проміжку дорівнює нулю:

, (2.75)

то функції утворюють в цьому проміжку ортогональну систему. Наприклад, сімейство тригонометричних функцій

утворюють ортогональною систему в проміжку .

Дійсно,

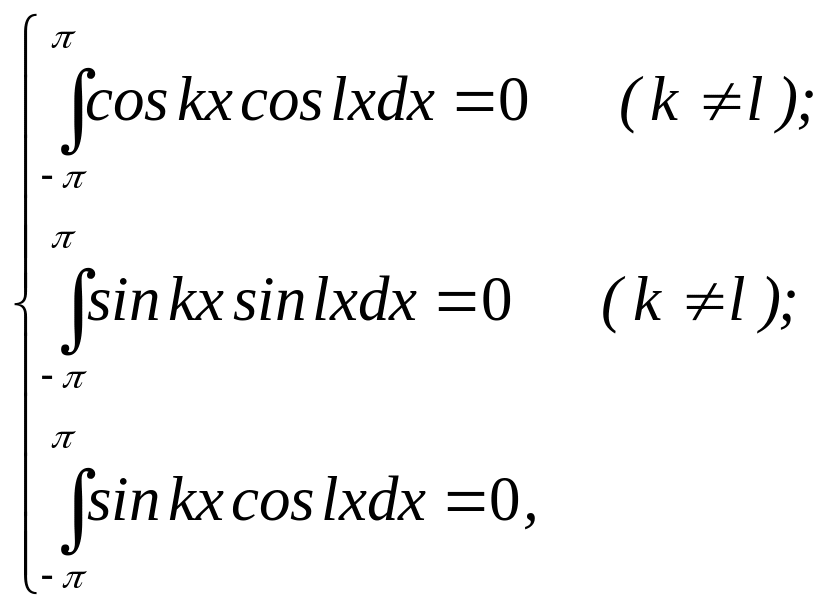
причому ці інтеграли вичерпують усі варіанти комбінування двох різних функцій сімейства.

На підставі леми з курсу математичного аналізу виходить: якщо одна з функцій тотожно дорівнює нулю, наприклад , то вона ортогональна до всіх без виключення функцій, оскільки в цьому випадку виконується умова (2.75).

Лінеаризоване рівняння задачі з визначення власних значень може бути подане у вигляді

, (2.76)

де і - однорідні лінійні диференціальні вирази.

Це рівняння тотожно дорівнює нулю при будь-яких значеннях, і, отже,

Тут інтеграл береться по всій довжині стрижня, і тому функція (2.76) ортогональна в проміжку до будь-якої функції.

Якщо розв’язок цієї задачі взяти у вигляді ряду

, (2.77)

де - довільні постійні, а - функції, що мають задовольняти граничні умови задачі, то функція (2.80) вже не буде тотожно дорівнювати нулю, а значить, і не буде ортогональною у вказаному проміжку до будь-якої функції. Можна, проте, зажадати, щоб вона була ортогональна хоча б до обмеженого класу функцій, наприклад функцій, що становлять ряд (2.81), тобто щоб

(2.78)

В результаті одержимо лінійних рівнянь для визначення постійних коефіцієнтів, що входять в ряд (2.77). З яких

(2.79)

де

Необхідною умовою мінімуму (2.79) буде

причому .

Якщо координатні функції утворюють повну систему функцій, то збільшення членів ряду (2.77) дозволяє знаходити необхідну кількість власних значень і відповідних їм власних функцій задачі з будь-яким степенем точності. При практичному використанні як метода Гальоркіна, так і метода Релея-Рітца доводиться обмежуватись невеликою кількістю членів ряду (2.77), тому точність рішення, як правило, визначається не повнотою системи координатних функцій, а тим, наскільки вдало вибрані перші члени цього ряду.

Усі міркування, приведені для функції одного аргументу, можна застосувати і до функцій двох аргументів і більше. Для вирішення задачі про вигин пластинок рівняння Гальоркіна можна подати у вигляді:

, , (2.80)

де замість лінійного проміжку розглядається плоска область, обмежена контуром пластинки, а функція, виражається таким подвійним рядом по області :

(2.81)

Необхідно, щоб наближена функція в рівняннях (2.83), що є лівою частиною диференціального рівняння зігнутої серединної поверхні пластинки, була ортогональна в області до всіх функцій ряду (2.84), що входять в цю наближену функцію.

Таким чином, метод Гальоркіна, як і метод Рітца, виходить з принципу можливих переміщень, тому обидва методи рівноцінні. У обох випадках апроксимуючу функцію необхідно вибирати так, щоб вона задовольняла хоча б геометричним граничним умовам.

Розділ 3

Стійкість прямих стрижнів при поздовжньому стисненні

Задачі стійкості пружних стрижнів добре вивчені і досить широко відомі. Мета цього розділу показати не специфіку завдань стійкості стрижнів, а те загальне, що властиво всім задачам стійкості тонкостінних пружних систем. Розглянуто докладне виведення основного лінеаризованого рівняння четвертого порядку, детальний опис зміни форм втрати стійкості стрижня на пружній основі і на пружних опорах, аналіз впливу деформацій зсуву на критичне навантаження і наближене дослідження закритичної поведінки стрижнів.