2.4 Метод Релея – Рітца в задачах стійкості

Метод Релея – Рітца є універсальним методом визначення екстремумів або стаціонарних значень функціоналів. Суть цього методу полягає в заміні задачі пошуку стаціонарних значень функціоналів принципово більш простою задачею пошуку стаціонарних значень функцій декількох змінних. Схему використання методу Релея – Рітца розглянемо на прикладі визначення критичної сили для стислого прямого стрижня. При цьому слід мати на увазі, що такий приклад вибраний тільки для наочності викладення і всі етапи розв’язання, міркування і висновки мають загальний характер. Енергетичний критерій стійкості у формі Брайана для прямого стрижня, стиснутого поздовжньою силою, має вигляд:

, (2.65)

де і згідно із залежністю (2.64)

(2.66)

Граничні умови для функції поперечного прогинання вважаємо заданими. Наприклад, у разі шарнірно опертого стрижня (рис.2.8 а) маємо такі граничні умови:

(2.67)

У своїй більшості задачі теорії пружності і теорії стійкості пружних систем зводяться до інтегрування диференціальних рівнянь із заданими граничними умовами Точного розв’язку деяких важливих для практики задач до цього часу не отримано, оскільки інтегрування диференціальних рівнянь, до яких вони зводяться, пов’язане з певними математичними труднощами. Метод Релея-Рітца дозволяє ефективно отримувати наближені розв’язки з точністю, що є достатньою для інженерних розрахунків.

При розв’язанні задачі методом Релея – Рітца функцію поперечного прогинання можна задати у вигляді ряду

(2.68)

де - вільні незалежні параметри (так звані базисні функції); - функції, що мінімум двічі диференціюються і задовольняють (кожна окремо) геометричні граничні умови. Для шарнірно опертого стрижня ці функції повинні задовольняти умови і

Підставивши ряд (2.68) у вираз (2.66) і виконавши необхідні операції диференціювання і інтегрування, перетворимо функціонал зміни повної потенціальної енергії стрижня у функцію незалежних змінних і параметра навантаження :

(2.69)

При цьому

Необхідна умова стаціонарності функції , якою замінений початковий функціонал, зводиться до системи рівнянь

(2.70)

Таким чином, отримали систему рівнянь, що є лінійною однорідною системою алгебраїчних рівнянь стосовно незалежних параметрів . У матричному записі ця система рівнянь має вигляд

(2.71)

де

; ;

причому

Умова існування розв’язків системи (2.71), що не дорівнюють нулю, зводиться до рівняння, з якого можуть бути знайдені власні значення навантаження :

(2.72)

Це рівняння ступеня дає власних значень , які приблизно відповідають першим точкам біфуркації початкового стану стійкої рівноваги стрижня. Найменше зі знайдених власних значень приблизно дорівнює критичному навантаженню, тобто .

Для кожного власного значення розв’язки рівняння (2.71) дають можливість з точністю до масштабу приблизно знайти форму зігнутої осі стрижня в околі точки біфуркації. Зокрема, розв’язок при приблизно описує форму зігнутої осі стрижня при втраті стійкості:

де .

При розв’язок задачі методом Релея – Рітца збігається до точного розв’язку, причому силові граничні умови задовольняються автоматично. Але при практичному використанні методу, коли число членів ряду (2.68) невелике, збіг до точного розв’язку має тільки теоретичне значення. Значно важливіше вдало вибрати вид перших членів цього ряду. У разі застосування методу Релея – Рітца функції повинні задовольняти тільки геометричні граничні умови. Проте вибираючи базисні функції при невеликому числі членів ряду (2.68), що утримуються при розв’язанні, бажано задовольняти не тільки геометричні, але й силові граничні умови (особливо для першого члена ряду).

Подання шуканої функції у вигляді ряду далеко не єдиний спосіб переходу від задачі визначення стаціонарних значень функціонала до задачі визначення стаціонарних значень функції декількох змінних. З цією метою функцію можна шукати серед сім’ї функцій, що задовольняють задані геометричні умови задачі і залежні від довільних параметрів:

(2.73)

де - незалежні параметри, причому геометричні граничні умови виконуються при будь-яких значеннях (розглянутий ряд (2.68) – окремий випадок такої сім’ї функцій). Підставивши (2.73) у вираз (2.66), знову отримаємо залежності типу (2.69), але структура функції буде інша.

Поставлену задачу визначення критичних навантажень і точок біфуркації можна виконати, не розглядаючи аналітичного вигляду шуканої функції .

У досліджуваному функціоналі всі похідні можна виразити через кінцеві різниці. Якщо стрижень розбити на рівних ділянок і операцію інтегрування у виразі (2.66) замінити підсумовуванням, отримаємо

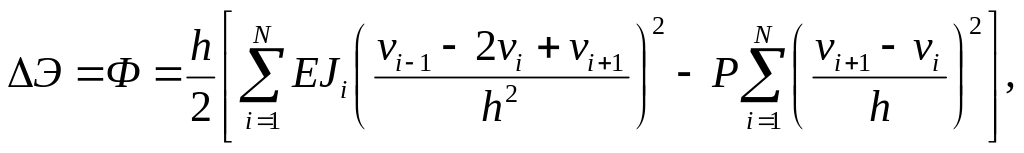
де - крок розбиття, а та - значення згинальної жорсткості і шуканої функції у вузлових точках. Геометричні граничні умови для шарнірно опертого стрижня дають: та . Розглядаючи значення , що залишилися як незалежні змінні, умова стаціонарності може бути подана у вигляді системи рівнянь

(2.74)

Умова існування розв’язків, що не дорівнюють нулю, знову приводить до рівняння типу (2.72), найменший корінь якого дає наближене значення . Відповідний цьому кореню розв’язок системи рівнянь (2.74) приблизно описує форму зігнутої осі стрижня при втраті стійкості. Рівняння (2.74) є рівнянням Ейлера для функціонала (2.66), записаним через кінцеві різниці. Тому намічений шлях розв’язання варіаційної задачі за допомогою кінцевих різниць фактично зводиться до розв’язання диференціального рівняння Ейлера методом кінцевих різниць.

У даний час є ряд модифікацій методу Релея – Рітца, спеціально пристосованих для чисельного рахунку на ЕВМ. Серед них необхідно зазначити метод скінчених елементів [3,4,5].