2.3 Енергетичний критерій стійкості у формі с.П. Тимошенко

Використання енергетичного критерію стійкості у формі Брайана потребує визначення початкових напружень в пружному тілі. При розв’язанні деяких задач стійкості іноді більш зручним виявляється енергетичний критерій в іншій формі, що не містить безпосередньо початкового напруження незбуреного стану рівноваги [1]. Розглянемо, як це можна реалізувати.

Стійкість рівноваги пружного тіла, навантаженого системою «мертвих» сил, будемо досліджувати з урахуванням припущень, зроблених у п. 2.2. Для опису збуреного стану рівноваги, суміжного з початковим незбуреним станом, знову скористаємося нескінченно малим параметром , що не залежить від координат. Але тепер відхилення точок тіла від їх початкових положень визначатимемо з точністю до включно. Тоді для переміщень точок тіла в новому відхиленому стані можна записати такі вирази:

(2.48)

де

- переміщення точок тіла в початковому незбуреному стані рівноваги;

; - скінченні функції координат.

Компоненти деформацій у новому збуреному стані рівноваги визначимо з точністю до доданків порядку :

(2.49)

Компоненти деформацій у початковому стані ,…, ,… визначатимемо за формулами (2.25), компоненти деформацій ,…, ,…, лінійно залежні від похідних , - за формулами (2.26). Величини будемо визначати за формулами

(2.50)

У цих формулах, як і у формулах (2.26), знехтувано доданками, що містять малі в порівнянні з одиницею множники типу і т.д. Ця точність обчислення деформацій відповідає введеній раніше моделі пружного тіла, яке до втрати стійкості напружене, але не деформоване.

У новому збуреному стані внутрішня потенціальна енергія тіла визначається залежностями (2.28) – (2.31) з тією різницею, що величини , що входять до залежності (2.31), визначаються за формулами (2.50). Потенціал зовнішніх сил

(2.51)

де - потенціал зовнішніх сил в початковому стані рівноваги:

(2.52)

Величина обумовлена переміщеннями :

(2.53)

Величина - переміщеннями :

(2.54)

Повну потенціальну енергію у збуреному стані подамо у вигляді

(2.55)

де складові внутрішньої енергії визначаються залежностями (2.30) і (2.31).

Зробивши перетворення, подібні до тих, що були зроблені в попередньому параграфі, енергетичний критерій стійкості (нехтуючи множником ) можна записати так:

(2.56)

де .

Причому у вираз для входять переміщення . Використавши залежність (2.45) і формули (2.50), з цього виразу можна виділити доданки, що містять переміщення . Тоді отримаємо , де

У значення включена решта всіх доданків, що не залежать від переміщень .

Величину можна розглядати як таку варіацію повної потенціальної енергії коли можливі переміщення збігаються з переміщеннями . Оскільки початковий стан рівноважний, при будь-яких переміщеннях сумісних з накладеними на тіло зв'язками. Зокрема, взявши переміщення такими, щоб вони дорівнювали нулю, з виразу (2.56) знову отримаємо вираз для енергетичного критерію стійкості у формі Брайана.

Переміщення можна підібрати так, щоб з виразу виключити початкове напруження

Використовуючи залежності закону Гука (2.4), введемо величини

Тоді вираз (2.31) для можна перетворити до вигляду

(2.57)

де

Як і у виразі (2.41), безпосередньо не залежить від початкового напруження або деформацій.

Для подальших перетворень скористаємося формулами інтегрування по частинах об'ємних інтегралів:

де - компоненти вектора зовнішньої одиничної нормалі до недеформованої поверхні даного тіла.

Виразивши компоненти початкових деформацій згідно з формулами (2.25) через початкові переміщення , отримаємо

(2.58)

Після інтегрування по частинах цей вираз набуде вигляду

де

(2.59)

компоненти напруження на поверхні даного тіла

Тепер з виразу для виключимо початкові переміщення. Для цього необхідно, щоб у всьому об'ємі тіла виконувалися рівняння

(2.60)

На тій частині поверхні тіла , для якої в явному вигляді задані поверхневі навантаження повинні виконуватися умови

(2.61)

Переміщення повинні бути сумісні з накладеними на тіло зв'язками, тому на тій частині поверхні тіла , для якої в явному вигляді задані початкові переміщення , завжди повинні виконуватися умови

(2.62)

При виконанні всіх наведених умов вираз (2.58) для приводиться до вигляду

Причому інтегрування проводиться тільки на тій частині поверхні тіла , для якої переміщення задані в явному вигляді.

Тепер вираз (2.57) можна записати в такому вигляді:

З урахуванням виразу (2.54) для зміну повної потенціальної енергії можна подати так:

(2.63)

де

Причому переміщення , що входять до виразу (2.63), не можна задавати довільно, а вони повинні задовольняти умови (2.60) – (2.62).

Таким чином, енергетичний критерій стійкості

(або при )

де зміна повної потенційної енергії підраховується за формулою (2.63), має назву енергетичного критерію у формі С.П. Тимошенко.

Ті умови, які були накладені на переміщення з метою виключення з виразу для початкового напруження і деформацій, можна трактувати таким чином. По – перше, величини де пов’язані з законом Гука, можна розглядати як компоненти напруження другого порядку малості, що виникають під час переходу тіла з початкового незбуреного стану рівноваги в новий збурений стан, для якого переміщення описується співвідношеннями (2.48). Тоді величини , введені за допомогою формул (2.59), можна вважати навантаженнями другого порядку малості, що виникають на поверхні під час переходу тіла в новий стан. По – друге, рівняння (2.60) можна розглядати як умови самоврівноваження напруження другого порядку малості. Умови (2.61) можна трактувати як граничні умови на тій частині поверхні тіла , для якої задані мертві зовнішні навантаження . Оскільки при переході в новий збурений стан зовнішні навантаження залишаються незмінними, додаткові поверхневі навантаження другого порядку малості на частині поверхні дорівнюють нулю. Додаткові поверхневі навантаження на частини поверхні можна розглядати як додаткові реакції зв'язків, що виникають під час переходу тіла в новий стан. Таке трактування найбільш природне для моделей механічних систем типу абсолютно жорстких стрижнів, з’єднаних пружними шарнірами, або стрижнів і кілець з нерозтяжною віссю.

Розглянемо, наприклад, систему з п.1.2 і визначимо її стійкість за допомогою енергетичного критерію.

Рисунок 2.6

Якщо скористатися енергетичним критерієм у формі С.П. Тимошенко, то відповідно до (2.63) можна записати (рис. 2.6)

де

При цьому можна вважати, що роль параметра , який фігурує в (2.48), відіграє кут . З умови критичного значення сили -

Енергетичний критерій стійкості у формі Брайана, в якому зміна повної потенціальної енергії системи виражається через початкове напруження або подовження, застосувати до даної системи не можна: стрижень вважається абсолютно жорстким, і при навантаженні енергія в ньому не акумулюється. Для того щоб при підрахунку зміни повної потенціальної енергії скористатися залежностями типу (2.45) або (2.46), необхідно ввести в дану систему додатковий пружний елемент, що акумулює енергію в докритичному стані рівноваги. Роль такого елемента може відігравати пружина жорсткості (рис. 2.7). Причому відповідно до взятих вище обмежень жорсткість пружини повинна бути чималою, щоб можна було знехтувати зміною довжини стрижня в докритичному стані.

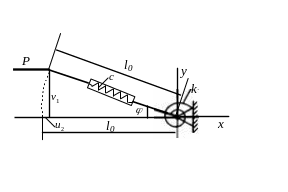
a) б)

Рисунок 2.7

Розглядаючи переміщення тільки першого порядку малості (рис. 2.7 а), що відповідають виразам (2.23), для визначення зміни повної потенціальної енергії можна скористатися залежністю типу (2.45):

де

Остаточний результат звичайно такий самий, як при розв’язанні задачі за допомогою енергетичного критерію у формі С.П. Тимошенко. При цьому критична сила не залежить від жорсткості пружини , як ейлерова критична сила для стиснутого стрижня не залежить від жорсткості стрижня на розтягування. Для порівняння на рис. 2.7 б показаний стрижень з пружиною жорсткості , відхилений відповідно до запису енергетичного критерію стійкості у формі С.П. Тимошенко.

Аналогічно у випадку, коли розглядається стійкість шарнірно опертого стрижня, стиснутого силою , і вісь стрижня вважається нерозтяжною, енергетичний критерій стійкості записують у формі С.П. Тимошенко (рис. 2.8 б):

де для визначення зближення кінців стрижня введемо криволінійнк координату , для якої . Інтегруючи останню рівність по довжині стрижня і нехтуючи малими другого порядку малості, отримаємо Оскільки в момент втрати стійкості , то

Якщо невідому форму вигину стрижня вибрати у вигляді ряду з довільними коефіцієнтами :

, (2.64)

який задовольняє усі граничні умови, то отримаємо залежність типу . Оскільки критичне навантаження – найменше навантаження при якому відбувається втрата стійкості, то з умови знайдемо .

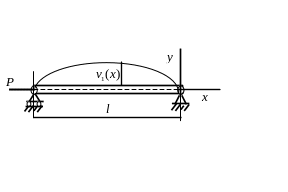
a) б)

Рисунок 2.8

Треба відзначити, що узявши для шарнірно опертого стрижня функцією прогинання лише перший член ряду (2.64) , з критеріїв Брайана і С.П. Тимошенко отримаємо точне значення критичної сили , таке саме, що було отримано через рівняння пружної лінії в п.1.1 або в п.1.5.1.

Перевагою енергетичного критерію у формі С.П. Тимошенко є те, що він описується через переміщення , які у подальшому можуть бути використані для наближеного опису закритичної поведінки пружних систем.