2.2 Варіаційний критерій визначення стійкості пружних систем

У лінійній теорії пружності компоненти подовжень виражаються через переміщення точок тіла за допомогою лінійних співвідношень Коші (2.9). Для розв’язання задач стійкості цих співвідношень недостатньо, оскільки задачі стійкості є нелінійними. Якщо у виразах подовжень разом з лінійними щодо переміщень доданками врахувати квадратичні доданки, то для компонентів подовжень можна отримати такі нелінійні співвідношення [1]:

(2.22)

Застосуємо ці співвідношення при дослідженні стійкості пружного тіла, навантаженого системою мертвих сил. Для простоти міркувань вважатимемо, що всі зовнішні сили змінюються пропорційно одному параметру , а накладені зв'язки, як і раніше, виключають переміщення тіла як жорсткого цілого.

Припустимо, що стан рівноваги навантаженого тіла, що відповідає розв’язку лінійної задачі, відомий. Цей стан надалі називатимемо початковим незбуреним станом рівноваги. Стійкість рівноваги цього стану будемо досліджувати при таких припущеннях.

1. Початковий незбурений стан рівноваги тіла описується рівняннями лінійної теорії пружності.

2. Змінами розмірів і форми тіла в початковому стані рівноваги можна повністю знехтувати.

3. Залежності закону Гука (2.3) справедливі не тільки для початкового стану, але і при малих відхиленнях тіла від початкового стану рівноваги.

Формулювання умов стійкості пружного тіла у варіаційному поставленні може бути отримане двома різними способами (див. п.1.5, 1.6). Перший спосіб ґрунтується на визначенні умов, при яких в околі початкового незбуреного стану рівноваги може існувати новий збурений стан рівноваги, тобто на визначенні варіаційним методом точок біфуркації початкового стану рівноваги. Другий спосіб пов'язаний із застосуванням теореми Лагранжа.

Розглянемо перший спосіб. Переміщення точок тіла в початковому незбуреному стані рівноваги вважатимемо відомими і позначимо

Тоді переміщення, що відповідають новому збуреному стану рівноваги, дорівнюватимуть

(2.23)

де - додаткові переміщення, які отримують точки тіла при переході з початкового незбуреного стану рівноваги в новий збурений стан рівноваги. При цьому функції вважатимемо скінченними, а коефіцієнт нескінченно малою величиною, що не залежить від координат. У новому стані рівноваги компоненти деформацій виразимо через переміщення (2.23) за допомогою співвідношень (2.22):

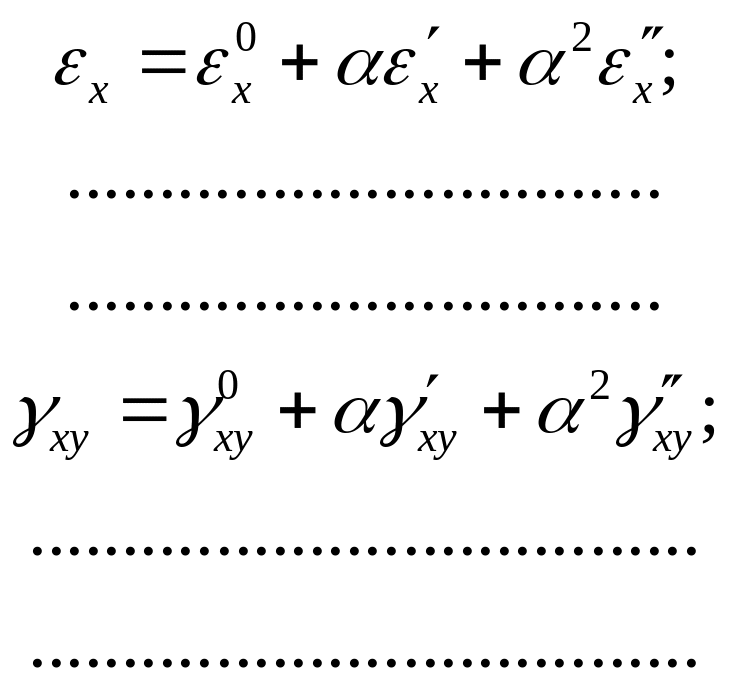(2.24)

де - компоненти деформацій у початковому стані рівноваги, що визначаються за допомогою лінійних співвідношень (2.9):

(2.25)

Вирази для мають таку структуру:

Оскільки відповідно до взятого припущення (див. п 1.8) зміною розмірів тіла в докритичному стані рівноваги можна знехтувати, замість останніх залежностей можемо використовувати такі вирази:

(2.26)

Величини - від квадратів похідних :

(2.27)

Таким чином, при дослідженні стійкості початкового незбуреного стану беремо таку модель: до втрати стійкості тіло напружене, але не деформоване.

Закон Гука вважаємо справедливим для станів, суміжних із початковим. Тому внутрішню потенціальну енергію в новому збуреному стані рівноваги можна обчислити за формулою (2.7), підставивши значення деформацій з (2.24). З точністю до доданків, що мають множник , отримаємо

(2.28)

де - потенціальна енергія деформації тіла в початковому стані рівноваги,

(2.29)

(2.30)

(2.31)

Потенціал зовнішніх сил у новому збуреному стані рівноваги визначимо за загальною формулою (2.10), враховуючи отримані залежності (2.23):

(2.32)

де - потенціал зовнішніх сил у початковому стані рівноваги,

(2.33)

(2.34)

Тоді вираз для повної потенціальної енергії матиме вигляд

(2.35)

де - повна потенціальна енергія в початковому стані.

Величина є першою спеціальною варіацією повної енергії в початковому стані рівноваги, тобто варіацією, при якій можливі переміщення збігаються з переміщеннями [2]. Оскільки така варіація є окремим випадком загальної варіації, то, очевидно, . Визначимо умови існування станів рівноваги, суміжних з початковим незбуреним станом. Новий збурений стан є рівноважним, якщо перша варіація повної потенціальної енергії в цьому стані дорівнює нулю, тобто

(2.36)

Оскільки початковий стан рівноважний, , і варіаційна умова існування нових станів рівноваги, суміжних з початковим, набуває вигляду

(2.37)

У співвідношенні (2.35) величина пропорційна другій спеціальній варіації (точніше ). Тому умову (2.37) іноді формулюють у вигляді такого варіаційного принципу [2]. Для існування рівноважних станів, суміжних з початковим станом рівноваги, необхідно, щоб друга спеціальна варіація повної потенційної енергії набувала стаціонарних значень, тобто

З цього варіаційного принципу або варіаційного критерію стійкості можна знайти власні значення параметра навантаження і власні функції задачі. Власними значеннями називають такі значення параметра при яких задача має розв’язки, що тотожно не дорівнюють нулю, а власні функції з точністю до масштабу визначають конфігурацію системи, що відповідає цим значенням .

Для того щоб з'ясувати, при яких значеннях початковий стан є стійким і при яких нестійким, можна скористатися другим шляхом виведення, отриманого раніше варіаційного принципу.

Згідно з теоремою Лагранжа початковий стан рівноваги стійкий тільки тоді, коли повна потенціальна енергія має мінімум. Таким чином, при будь-яких можливих відхиленнях системи в околі стійкого стану рівноваги повинна виконуватися умова

. (2.39)

Критичним є таке значення параметра навантаження , при перевищенні якого початковий стан рівноваги перестає бути стійким. Тому при умова (2.39) для будь-яких можливих відхилень не виконується і, взагалі кажучи, є такі відхилення, при яких . Отже, це нижня межа тих значень , при яких можливі відхилення системи від початкового стану, що приводять до умови .

Слід підкреслити, що при повна потенціальна енергія початкового стану не стає максимальною, а тільки перестає бути мінімальною. Тому при , окрім відхилень, що приводять до , можливі відхилення, при яких та .

Враховуючи, що з виразу (2.35) отримуємо

(2.40)

Позначимо

(2.41)

де

тут - компоненти деформацій початкового стану при .

Тоді для тих відхилень, при яких з (2.40) можна записати

. (2.42)

Остання залежність визначає умову мінімуму навантаження і знову приводить до варіаційного рівняння (2.37), еквівалентного (2.38). Дійсно, з умови

отримуємо

З урахуванням залежностей (2.42) і (2.41) остання рівність приводить до варіаційного рівняння (2.37). Тепер стає зрозумілим, що перше власне значення параметра навантаження , яке визначається з цього рівняння, збігається з нижньою межею значень , які визначаються залежністю (2.42), тому

З викладеного випливає практичне правило визначення критичних навантажень. Для визначення критичного значення параметра навантаження , потрібно визначити зміну повної потенційної енергії системи з точністю до квадратів переміщень, що описують перехід системи в новий, відхилений стан, суміжний з початковим станом рівноваги, стійкість якого досліджується. Власні значення параметра навантаження можна знайти або з умови стаціонарності :

(2.43)

або з умови

(2.44)

з додатковою умовою мінімуму параметра навантаження . Перше власне значення дорівнює критичному значенню , а перша власна функція задачі описує конфігурацію системи у момент втрати стійкості.

Формулу для можна перетворити, виразивши доданок не через початкові подовження, а через початкові напруження. Скориставшись залежностями закону Гука (2.3), отримаємо

де ,…, ,… - компоненти початкових напружень при . Вираз для перепишемо ще раз, знехтувавши множником :

(2.45)

Початкові напруження , , … повинні бути заздалегідь визначені за допомогою розв’язання лінійної задачі для початкового незбуреного стану рівноваги тіла. Подовження і визначаємо за формулами (2.26) і (2.27). Якщо за залежностями закону Гука у формі (2.4) ввести величини

то вираз (2.45) можна записати в такому вигляді:

(2.46)

Варіаційна умова (2.43) або (2.44), виражена через початкові напруження за допомогою залежностей типу (2.45) або (2.46), виражає енергетичний критерій стійкості (варіаційний принцип) у формі Брайана.

З виразу (2.45) випливає, що при стан рівноваги тіла завжди є стійким, оскільки перший інтеграл цього виразу більше нуля за будь-яких комбінацій відхилень переміщень . Величина може перетворитися на нуль, і початковий стан рівноваги може стати нестійким тільки при значеннях , що перевищують деяке критичне значення .

Оцінимо порядок значень початкового напруження і деформацій, при яких це може відбутися. Порівнюючи формули (2.26) і (2.27), бачимо, що порядок дорівнює порядку . Тоді з залежності (2.45) випливає, що для того щоб могло обернутися на нуль, порядок значень початкового напруження повинен бути такий самий, як і модуля пружності. Іншими словами, для того щоб початковий стан рівноваги ізотропного пружного тіла перестав бути стійким, його початкові деформації повинні мати порядок одиниці. У цьому випадку все викладене вище стає неправильним, оскільки при виведенні основних співвідношень початкові деформації вважалися нехтовно малими в порівнянні з одиницею. Відомо два винятки, при яких порушується наведена загальна оцінка значень критичних деформацій. Це тіла з різко вираженою анізотропією пружних властивостей і тонкостінні тіла (стрижні, пластини, оболонки).

На рис. 2.4 зображений паралелепіпед з анізотропного матеріалу, рівномірно стиснутий уздовж осі x. Початковий напружений стан вважаємо одноосним, причому де - площа поперечного перетину паралелепіпеда. Матеріал має настільки різко виражену анізотропію, що де - відповідно модуль зсуву в площині і модуль пружності у напрямі осі . У такого паралелепіпеда можлива зсувна форма втрати стійкості в площині при малих початкових деформаціях Переміщення при цій формі втрати стійкості задамо у вигляді Скористаємося залежністю (2.46). Хоча вона й виведена для ізотропного тіла, але, як показано в [1], вона дійсна і для анізотропного тіла

Рисунок 2.4

За формулами (2.26) і (2.27) визначимо

Враховуючи залежність закону Гука для дотичних напружень можна записати

де - об'єм паралелепіпеда.

Із умови випливає, що критичне напруження визначається за формулою

Як бачимо, абсолютне значення критичного стискаючого напруження не залежить від розмірів тіла і дорівнює модулю зсуву в площині . Через взяте припущення про різко виражену анізотропію пружних властивостей втрата стійкості відбувається при малих абсолютних значеннях початкової деформації

Як другий приклад розглянемо шарнірно опертий прямий стрижень, стиснутий силою (рис 2.5).

Рисунок 2.5

Як і в попередньому прикладі, початковий напружений стан вважаємо одноосним, тобто де - площа поперечного перетину стрижня. Згинальний стан рівноваги стрижня, суміжний із початковим, опишемо за допомогою звичайної гіпотези плоских перетинів. Тоді можна записати

У даному випадку згідно із залежністю (2.46) маємо

За формулами (2.26) та (2.27) знаходимо

За законом Гука , отже,

.

Після інтегрування за площею поперечного перетину стрижня отримаємо

(2.47)

де - статичний момент інерції поперечного перетину.

Втрата стійкості шарнірно – опертого стрижня відбувається по одній напівхвилі синусоїди (див. п. 1.5.1), тому припустимо, що Тоді

З останнього виразу випливає, що

де - радіус інерції поперечного перетину.

Для тонких стрижнів тому першим доданком у квадратних дужках можна знехтувати в порівнянні з одиницею і, враховуючи, що , з умови отримати значення ейлерової критичної сили значення якої було знайдено за допомогою лінеаризованих рівнянь в п. 1.5.1.

Нехтуючи знаком, підрахуємо відносне подовження (укорочення) стрижня, обумовлене :

Для тонких стрижнів критична деформація дійсно виявляється малою. Слід ще раз підкреслити, що критична деформація є геометричною характеристикою стрижня і не залежить від характеристик пружності матеріалу.

Закінчуючи, необхідно зробити таке зауваження. З наведеного виведення формули Ейлера випливає, що ця формула органічно містить похибку порядку в порівнянні з одиницею. Ці висновки були зроблені в п. 1.8 без допомоги енергетичного критерію стійкості. Похибки такого самого типу містяться в усіх формулах для критичних навантажень тонкостінних пружних систем, якщо при виведенні формул початкові деформації вважають нехтовно малими в порівнянні з одиницею.