27. Неравенство Клаузиуса

С помощью принципа Карно второму началу термодинамики можно

придать следующую количественную формулировку.

Если система, совершая циклический процесс, получает теплоту Q_i от теплового резервуара R_i с температурой T_i (i = 1, 2, ..., n), то справедливо неравенство

 ≤ 0. (27.1)

Его называют неравенством Клаузиуса. В случае двух тепловых резервуаров оно следует непосредственно из тех результатов, которые получены раньше (из формул (23.1–23.3), (24.1), (25.4)):

η = 1 + Q₂ /Q₁ ≤ 1 – T₂ / T₁   Q₁ / T₁ + Q₂ / T₂ ≤ 0.

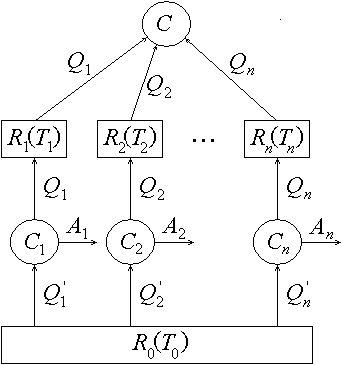
Для доказательства неравенства Клаузиуса в общем случае вводятся в рассмотрение вспомогательные источник теплоты R₀ с температурой T₀ и обратимые циклы Карно C_i, i = 1, 2, ..., n (рис. 12). Цикл C_i действует между резервуарами R₀ и R_i. Пусть Q_i' – теплота, получаемая в этом цикле от R₀, а A_i – совершаемая работа. И пусть при этом резервуару R_i передается теплота Q_i, равная по величине теплоте, получаемой от R_i в исходном цикле C. Для цикла C_i выполняются соотношения

Рис. 12

A_i = Q_i' – Q_i, Q_i' = Q_i  T₀ / T_i.

В исходном цикле совершается работа

A = .

Пусть теперь исходный и вспомогательный циклы действуют вместе, совершая сложный круговой процесс. Последовательные его этапы таковы. Вначале система совершает исходный циклический процесс (цикл C на рис. 12). Затем она теплоизолируется, после чего совершаются вспомогательные циклы. Далее все повторяется.

В результате сложного процесса резервуары R_i сколько теплоты получат, столько же ее и отдадут (их состояние не изменится). Из резервуара R₀ поглощается количество теплоты

Q₁' + Q₂' + ... + Q_n' = ,

за счет чего совершается работа

A +  =  = T₀ .

Согласно второму началу в формулировке Томсона, эта работа не может быть положительной. Она или равна нулю, или отрицательна. И так как температура T₀ положительна, неравенство (27.1) тем самым доказано. Использование вспомогательных приспособлений (обратимых машин Карно и теплового резервуара R₀) никак не отражается на справедливости неравенства (27.1): они привлекаются только после завершения исходного циклического процесса.

Соотношение (27.1) доказано для случая, когда резервуары R_i велики

и температуры T_i могут считаться постоянными. Общий случай конечных резервуаров при произвольном изменении во времени температуры сводится к разобранному. Действительно, пусть температура T_i резервуара R_i меняется во времени. Процесс теплообмена, в результате которого резервуар R_i отдает системе теплоту Q_i, можно разбить на сколь угодно большое число N элементарных процессов, в которых резервуар R_i отдает бесконечно малые количества теплоты δQ_i1, δQ_i2, ..., δQ_iN. В каждом элементарном процессе температуру резервуара R_i можно считать постоянной. Один резервуар R_i с переменной температурой как бы эквивалентен N последовательно включаемым резервуарам с постоянными, но разными температурами. В течение короткого времени только один резервуар (пусть j-й) из этой последовательности отдает системе теплоту δQ_ij, остальные теплоизолированы. Поэтому в общем случае неравенство Клаузиуса следует писать в виде

 ≤ 0. (27.2)

Здесь индекс e у температуры указывает, что это температура окружающей среды, а не системы (в случае обратимого цикла обе температуры при тепловом контакте равны, и индекс e можно опустить). Знак равенства имеет место для обратимого циклического процесса, неравенства – для необратимого процесса.