26. Метод циклов

Создание абсолютной термодинамической шкалы температур не единственный результат применения принципа (теоремы) Карно. На этом принципе основан метод циклов. Суть его в следующем. Исследуемая система используется в качестве рабочего вещества в обратимой машине Карно. Разница между температурами нагревателя и холодильника берется бесконечно малой. Применение принципа Карно позволяет получить информацию о системе.

В качестве примера рассматривается физически однородное тело, состояние которого характеризуется двумя параметрами. Пусть это будут T и V. Внутренняя энергия тела есть однозначная функция этих параметров: U = U(T, V). Считается известным термическое уравнение состояния (8.1). Тогда принцип Карно позволяет найти зависимость внутренней энергии U тела от его объема V.

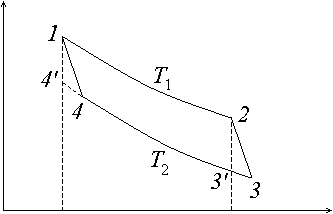
Для этого тело используется как рабочее вещество в произвольном обратимом цикле Карно. Единственное ограничение на цикл: температуры нагревателя и холодильника различаются на малую величину ΔT (ΔT = T₁ –T₂  0).

p
	V1 V2 V
	Рис. 11

Итак, температура T₁ и, следовательно, изотерма 1–2 произвольные (рис. 11). Точки 1 и 2 на ней также случайные. В соответствии с принципом Карно для цикла 1234 имеет место соотношение

A /Q₁ = ΔT / T₁.

Работа A равна площади цикла. С учетом того, что изотермы 1–2 и 4–3 близки (ΔT мало), эта площадь при вычислении работы заменяется на площадь криволинейного четырехугольника 123'4', где стороны 1–4' и 2–3' являются изохорами. Эта замена вносит пренебрежимо малую погрешность (искомая площадь – величина первого порядка малости по ΔT, у криволинейных треугольников 144' и 233' площадь – второго порядка малости, а они к тому же заменяются один на другой). В результате

A =     .

Если выражение под интегралом поделить и умножить на ΔT , то опять же с точностью до малых второго порядка

A  ΔT .

При расширении по изотерме 1–2 (T = T₁, dV > 0) к телу подводится теплота

Q₁ = .

Бесконечно малое приращение внутренней энергии из-за столь же малого изменения объема можно представить в виде

dU(T₁, V) = (U / V)_TdV,

так что

Q₁ = .

Подстановка A и Q₁ в исходное уравнение для бесконечно малого цикла Карно дает (после освобождения от знаменателей и сокращения на ΔT)

.

При произвольном выборе изотермы 1–2 и начальной и конечной точек на ней интегралы равны, если равны подынтегральные выражения:

T(p / T)_V  = (U / V)_T + p,

или

(U / V)_T  = T(p / T)_V   – p. (26.1)

Индекс у температуры опущен в силу ее произвольности.

Данная формула решает поставленную задачу.

Используя эту формулу, разности теплоемкостей c_p и c_V  из соотношения (15.4) можно придать вид

c_p – c_V  = T(p / T)_V(V / T)_p. (26.2)

Итак, если термическое уравнение состояния известно, то можно найти зависимость внутренней энергии от объема, а используя (26.2), вычислить разность теплоемкостей c_p и c_V. Для идеального газа термическое уравнение состояния имеет вид pV = νRT и

(U / V)_T = 0, а c_p – c_V = R.

Здесь теплоемкости c_p и c_V молярные. Таким образом, для идеального газа внутренняя энергия не зависит от объема (закон Джоуля) и справедливо соотношение Майера.