Кинетика процессов утилизации субстрата, образования продуктов метаболизма и биомассы в культурах клеток

Идеальные реакторы для изучения кинетики клеточного роста

Если небольшое количество живых клеток поместить в раствор, содержащий все необходимые питательные вещества, то при определенных температуре и рН клетки будут расти. В зависимости от морфологии клетки процесс ее роста может происходить двумя путями. Одноклеточные организмы претерпевают в процессе роста деление, и поэтому увеличение их биомассы (массы живых организмов) сопровождается увеличением числа клеток. Основное внимание в настоящей главе будет уделено именно этому типу роста; здесь мы встретимся с проблемой роста популяции. Совершенно по-иному происходит рост плесневых грибов — в этом случае по мере роста организма возрастают в первую очередь длина и число гиф мицелия. Таким образом, в культуре растущей плесени увеличиваются размеры организмов и их концентрация, но не обязательно число организмов.

С клеточным ростом тесно связаны два других процесса: поглощение клеткой некоторых веществ из окружения и выделение конечных продуктов метаболизма клетки в среду. Как мы увидим ниже, в процессе роста скорости этих процессов изменяются в очень широких пределах. В общем случае предсказать эти скорости не представляется возможным; вместе с тем весь многолетний опыт говорит о том, что среди множества известных процессов с участием культур клеток достаточно часто встречается только ограниченное число типичных путей утилизации субстрата и образования продуктов жизнедеятельности клеток. Изучив сначала эти типичные пути, мы будем лучше подготовлены к решению новых задач, связанных с применением культур растущих клеток.

Необходимая и достаточная точность (а следовательно, и сложность) математического описания кинетических свойств системы в свою очередь зависит от ее сложности и предполагаемой области применения математических выражений. Прежде чем перейти к анализу конкретных процессов и соответствующих математических выражений, описывающих их кинетику, мы должны иметь определенное представление о разнообразии реакций и процессов в популяции клеток. В нашем обсуждении основное внимание будет уделено клеточному росту, но аналогичные принципы, концепции и ход рассуждений применимы и к другим аспектам изучения химических процессов в клетке.

Начнем с самого сложного случая — с анализа растущей популяции клеток в самом общем виде. Затем рассмотрим, какие упрощения можно допустить в этом анализе и в каких ситуациях эти упрощения оправданны. На рис. 7.1 перечислены некоторые параметры, явления и взаимодействия, влияющие на кинетику роста популяции клеток.

П ри этом прежде всего следует усвоить, что во всех случаях нужно учитывать две взаимодействующие системы — биологическую фазу, состоящую из популяции клеток, и фазу, окружающую эту популяцию, или среду. Клетки поглощают питательные вещества и превращают субстраты (взятые из среды) в продукты метаболизма. Клетки генерируют теплоту, а температура среды в свою очередь определяет температуру клеток. Среда оказывает механическое воздействие на клетки посредством гидростатического давления или гидродинамических эффектов, а также путем изменения вязкости среды вследствие накопления клеточной массы и продуктов жизнедеятельности клеток.

Что касается среды, то из ряда ее важнейших характеристик прежде всего следует отметить многокомпонентноcть: во-первых, она должна содержать все необходимые для роста клеток питательные вещества, и, во-вторых, в ней накапливаются (по мере роста клеток) различные конечные продукты клеточного метаболизма. Химические реакции могут происходить и в среде, что приводит к модификации продуктов метаболизма, как, например, при гидролизе пенициллина. Часто клетки потребляют или продуцируют вещества, изменяющие кислотность среды; взаимосвязь клеточных процессов с кислотно-основным равновесием определяет рН среды, который в свою очередь влияет на клеточную активность и на процессы транспорта. В ходе клеточных реакций могут происходить изменения температуры, ионной силы, рН и реологических свойств бульона во времени.

Часто среда представляет собой многофазную систему, состоящую из жидкой фазы и диспергированных в ней пузырьков газа или из двух несмешивающихся жидких фаз, а иногда из одной газовой и двух жидких фаз. К числу последних достижений в разработке биореакторов относятся методы одновременного проведения клеточных реакций и процессов разделения путем введения в среду особых веществ, способствующих образованию дополнительной жидкой или твердой фазы. Наконец, в силу большого объема биологического реактора, высокой вязкости и неньютоновской природы бульона в отдельных его точках могут создаться разные условия. Все эти параметры и переменные среды существенно влияют на кинетику клеточного роста.

Что же касается наиболее важных особенностей популяции клеток, то, как мы уже знаем из предыдущих глав, каждая индивидуальная клетка представляет собой сложную многокомпонентную систему, которая даже на клеточном уровне далека от гомогенности. В каждой клетке одновременно осуществляется множество химических реакций, управляемых сложным комплексом систем регуляции. Благодаря этим системам клетка может изменять (и изменяет на самом деле) скорость и даже тип происходящих в ней химических реакций в зависимости от условий и состава среды. Длительное культивирование клеточной популяции может сопровождаться накоплением спонтанных мутаций; кроме того, особенности технологического процесса могут налагать давление отбора, приводящее к медленным изменениям генетической природы штамма.

С другой стороны, в культуре растущих клеток всегда наблюдается существенная гетерогенность популяции, т.е. в любой момент, в любом, даже самом малом объеме культуры индивидуальные клетки различаются по возрасту (одни только что образовались в результате деления, другие уже достигли состояния зрелости, а третьи находятся в стадии деления) и, следовательно, по биохимической активности. Из предыдущей главы, посвященной особенностям клеточного цикла, мы знаем, что различающиеся по возрасту клетки часто обладают различными метаболическими функциями и активностями.

Очевидно, практически невозможно создать кинетическую модель, которая учитывала бы все параметры и факторы, перечисленные на рис. 7.1. Поэтому теперь рассмотрим ряд приближений, которые позволяют упростить эту картину и найти математические выражения, описывающие кинетику роста популяции клеток.

Во-первых, что касается среды, то обычно допускают, что, за исключением одного компонента, все ее составляющие присутствуют в таких высоких концентрациях, что их изменения практически не отражаются на общих скоростях процессов. Таким образом, один компонент среды становится питательным веществом, лимитирующим скорость клеточного роста, и при анализе влияния состава среды на кинетику роста клеток мы должны учитывать концентрацию только этого компонента. Иногда возникает необходимость в учете некоторых других составляющих среды, например накапливающегося в среде ингибитора, в противном случае наше описание кинетики было бы слишком далеким от истинной картины. В отношении других параметров среды часто можно допустить, что их изменения не влияют в сколько-нибудь существенной степени на кинетику роста микроорганизмов за тот период, в течение которого проводится типичный эксперимент или осуществляется типичный процесс, если эти изменения не превышают обычных для этого эксперимента или процесса пределов. К тому же системы контроля и регулирования биореакторов могут поддерживать на постоянном уровне целый ряд параметров среды, в том числе рН, температуру и концентрацию растворенного кислорода. Впрочем, в некоторых случаях для адекватного описания требуемого диапазона кинетического поведения может возникнуть необходимость учета в модели многокомпонентности и нескольких параметров среды.

На рис. 7.2 суммированы основные принципы различных приближений и способов описания, которые могут быть полезны при математическом анализе клеточной фазы системы. Согласно этой схеме, разработанной Фредриксоном и Цучия, подходы к анализу микробиологических систем классифицируются в соответствии с числом компонентов, используемых при описании клеток, а также в зависимости от того, рассматриваются ли клетки как гетерогенная популяция различных объектов (как оно и есть на самом деле) или как популяция некоторых усредненных клеток (в этом случае клетки принципиально не отличаются от какого-либо компонента в растворе). Многокомпонентные модели клеток называют структурированными, а однокомпонентные - неструктурированными. Описание популяции клеток с учетом их гетерогенности называют сегрегированным подходом, а в несегрегированном описании рассматривают только усредненные свойства клеток.

К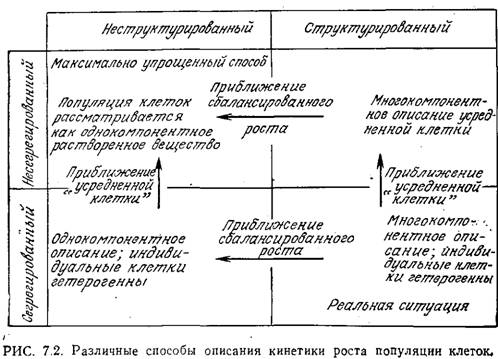 ак показано на рис. 7.2, реальная ситуация отвечает структурированной сегрегированной системе. Если гетерогенность клеток не влияет в существенной степени на кинетику исследуемых процессов, то можно принять «приближение усредненной клетки» и тем самым упростить способ описания от сегрегированного до несегрегированного. В так называемом состоянии «сбалансированного роста» вся синтетическая активность клеток скоординирована таким образом, что на средний состав клеток пролиферация популяции не влияет. В этом случае допустимо использовать модели, не учитывающие многокомпонентную природу клеток. Как мы увидим ниже, при анализе и описании роста популяций клеток обычно принимают наиболее идеализированную ситуацию, т. е. несегрегированную, неструктурированную модель.

С другой стороны, мы познакомимся с рядом таких ситуаций, когда выгоднее рассматривать биологическую фазу как более сложную систему. Так, в нестационарном состоянии (типичном, в частности, для периодических микробиологических процессов) условия сбалансированного роста даже в первом приближении соблюдаются только в течение сравнительно короткого промежутка времени. Хорошо известно, что в ходе периодического процесса в очень широких пределах могут изменяться как клеточный состав популяции, так и скорости и типы реакций, осуществляющихся в этой популяции, и тогда могут пригодиться более детальные модели. Кроме того, структурированные модели позволяют отражать непосредственно в математических выражениях известные особенности сети клеточных биохимических реакций. Аналогично не представляющее особых затруднений включение в модель кинетики клеточного роста особенностей клеточного цикла (сегрегированный подход) способствует повышению ценности и расширению диапазона применимости модели. Важнейшими элементами сегрегированных моделей являются кинетика и особенности регуляции роста индивидуальной клетки.

Живые клетки представляют собой чрезвычайно малые системы, поэтому количество любого химического компонента в них крайне ограничено. Действительно, приведенные в табл. 5.6 величины очень малы по сравнению с обычным для химика числом молекул порядка 10²³. Предельным случаем является ДНК, которая в медленно растущей бактерии содержится только в количестве одной молекулы; очевидно, что в этом случае само понятие «концентрация ДНК в клетке» становится весьма неопределенным. То же самое можно сказать о содержащихся в следовых количествах ионах, органоидах и многих других компонентах клетки. Хотя в некоторых из рассматриваемых ниже моделей мы будем описывать внутриклеточные события как непрерывные, следует отдавать себе отчет в том, что такое описание является всего лишь удобным приближением типичной усредненной клетки в популяции клеток (см. ниже). Реакции и процессы массопередачи, в которых участвует ограниченное число молекул, должны рассматриваться как случайные события. Для описания таких событий создавались стохастические модели популяций клеток, не имеющих существенных преимуществ по сравнению с более простыми детерминистическими моделями. Предсказуемость поведения популяции клеток можно проиллюстрировать, например, оценив точность детерминистического описания очень малой популяции, в частности типичного инокулята (посевного материала; обычно около 10⁵ клеток). Пусть совокупность продолжительностей клеточных циклов индивидуальных клеток описывается нормальным распределением:

Примем t=1, а стандартное отклонение Ϭ равным 0,5. Тогда мы можем сказать, что с коэффициентом доверительности 0,95 продолжительность клеточного цикла отдельной клетки составляет одна клетка = t± 1,96 Ϭ = 1,0±0,98

Далее рассмотрим суспензию, содержащую достаточно большое число клеток, например m клеток. Пусть каждая из m клеток растет независимо от других клеток, т. е. клеточная суспензия содержит m независимых образцов. Тогда 95%-ный доверительный предел времени удвоения численности этой популяции будет равен 2 Ϭ. Популяция, где

Следовательно, с возрастанием m неопределенность времени удвоения численности популяции быстро уменьшается. Приняв, например, как и раньше, Ϭ = 0,5 и t=l,0, легко найти, что 95%-ные доверительные пределы для t в случае популяции из m клеток составляют

В сущности, этот несложный расчет еще раз подтверждает известное положение, что, как и в любых стохастических процессах при относительно большом числе событий (например, в химических реакциях или в явлениях, связанных с транспортом жидкостей), изменения характеристик популяции могут быть предсказаны с достаточно большой точностью, даже если стандартные отклонения характеристик индивидуальных клеток велики. Так, рост инокулята, приводящий к повышению концентрации с 10⁴ до 10⁸ клеток в 1 мл, очевидно, обеспечивает достаточное усреднение по всем стадиям роста, что позволяет с высокой точностью определить время удвоения численности популяции.

Точно так же можно достаточно обоснованно говорить о скорости синтеза ДНК в типичной клетке популяции, хотя в каждой индивидульной клетке синтезируется только одна или две молекулы ДНК со скоростью, которая в данный момент может резко отличаться от средней величины.

Невозможно обсуждать кинетику в отсутствие данных о конструкции реактора для измерения скоростей процессов и оценки их кинетики. В следующем разделе мы вкратце рассмотрим соответствующие материальные балансы для двух типов идеальных биореакторов. Затем мы приступим к анализу кинетики клеточного роста, начиная с ситуации, схематично изображенной в верхнем левом углу рис. 7.2, т. е. с простейших моделей кинетики клеточного роста, утилизации субстрата и образования продуктов метаболизма. В последующих разделах главы мы изучим другие ситуации, также изображенные на рис. 7.2, и попытаемся оценить важность различных концептуальных и математических подходов к анализу кинетики роста популяции клеток. В общем случае разработка кинетической модели популяции клеток является своего рода искусством, требующим, во-первых, учета окончательной цели, для которой эта модель предназначается, во-вторых, тщательно продуманного и обоснованного выбора основных переменных и параметров, влияющих на наиболее важные процессы, и, в-третьих, известной концептуальной и математической гибкости, что необходимо для перевода качественных характеристик системы на язык применимых в практической деятельности математических выражений.

Получить полезную информацию о кинетике роста популяции микроорганизмов практически невозможно, если условия в разных участках объема реактора не идентичны. Поэтому желательно изучать кинетику только в реакторах с полным перемешиванием. Здесь мы изучим реакторы с полным перемешиванием периодического действия и проточные (непрерывного действия) реакторы.

Идеальный реактор периодического действия

Основой многих биохимических процессов является периодический рост популяций клеток, при котором после посева инокулята живых клеток в жидкую среду к последней в течение всего периода роста ничего не добавляется и из нее ничего не выделяется (за исключением, быть может, некоторых газов). Обычно в таком реакторе по мере роста популяции изменяются концентрации питательных веществ, клеток и продуктов метаболизма.

М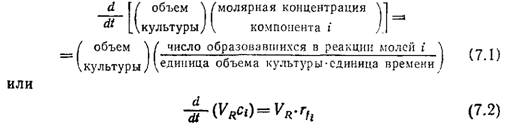 атериальный баланс по компоненту i показывает, что скорость его накопления, выраженная в виде производной общего количества компонента i по времени, должна быть равна скорости его образования, обусловленного химическими реакциями в реакторе. Таким образом,

где V_R — объем культуры;

с-количество молей i в единице объема культуры;

r_f — количество образовавшихся в реакции молей i в единице объема культуры за единицу времени.

Если в реактор не добавляют и из него не отбирают никаких жидких веществ и если потерями жидкости с потоком газа можно пренебречь, то V_R постоянно и уравнение (7.2) упрощается:

dc_i/dt=r_fi

Следует отметить, что аналогичными уравнениями может быть выражено не только изменение количества молей, но и массы или концентрации (плотности) компонента. Если же компонент i входит в состав газового потока, поступающего в реактор (или выходящего из реактора), то указанные выше уравнения должны быть дополнены слагаемыми, отражающими результирующую скорость поступления компонента i с газовой фазой.

Из уравнения (7.3) следует, что определение скорости изменения концентрации компонента i позволяет непосредственно определить общую скорость образования i в реакциях (в том числе внутриклеточных), которые происходят в реакторе периодического действия. В общем случае скорость образования r_fi зависит от состояния клеточной популяции (состава, морфологии, распределения по возрасту и т. д.) и всех параметров среды, оказывающих влияние на скорости реакций в клетках и среде. В то же время, как мы уже упоминали во введении к этой главе, обычно кинетику клеточного роста описывают упрощенно, принимая во внимание только наиболее важные параметры. В последующих разделах мы увидим, каким образом стехиометрия реакций и их скорости связаны со скоростью образования продуктов жизнедеятельности клеток.

Идеальный проточный реактор с полным перемешиванием (ПРПП)

На рис. 7.3, а изображены основные узлы лабораторного проточного реактора с полным перемешиванием (ПРПП), а на рис. 7.3, б указаны основные обозначения, используемые при моделировании и анализе такого рода реакторов. Если эти реакторы предназначены для изучения роста культур клеток, то их часто называют хемостатами. Как показано на этих рисунках, перемешивание осуществляется с помощью мешалки, потока восходящих пузырьков газа или того и другого. Примем, что в ПРПП перемешивание культуральной жидкости осуществляется настолько эффективно, что каждая фаза содержимого реактора вполне однородна по составу, т.е. концентрации любых компонентов в любой из фаз одинаковы во всем объеме реактора. Как показано на схеме, отсюда следует важный вывод о том, что состав вытекающего потока не отличается от состава содержимого реактора.

П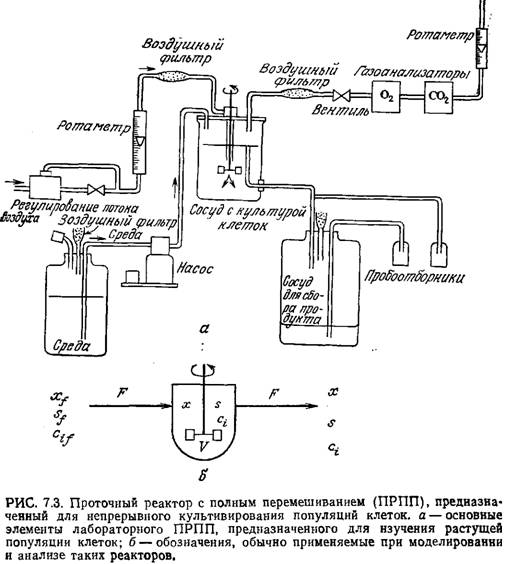 олное перемешивание должно обеспечивать и одинаковую концентрацию растворенного кислорода во всем объеме жидкой фазы. Этот факт особенно важен при анализе аэрируемых ПРПП, поскольку отсюда следует, что в большинстве случаев мы можем изучать происходящие в реакторе процессы независимо от конструкций аэратора или мешалки. Если система аэрации обеспечивает такую концентрацию растворенного кислорода, которая не лимитирует клеточный рост в ПРПП, то анализ кинетики клеточного роста мы можем рассматривать как независимую проблему. Аналогичные соображения применимы и к проблемам теплопередачи, которые могут возникать, в ходе роста микроорганизмов. Систему можно считать изотермической, если реактор снабжен устройствами для полного перемешивания, эффективного отвода тепла и регулирования температуры на заданном уровне; тогда можно изучать процессы микробиологических превращений в изотермических условиях.

В большей части последующего материала мы будем принимать все указанные допущения. В стационарном состоянии, когда концентрации всех компонентов в реакторе не изменяются во времени, к любому компоненту системы применимо следующее уравнение:

Обозначив, как и раньше, символом V_R общий объем культуры в реакторе, указанное уравнение стационарного состояния можно записать в следующем виде:

где F — объемная скорость потока раствора питательных веществ и вытекающего потока; с_if — молярная концентрация компонента i в потоке питательных веществ; с_i — концентрация компонента i в реакционной смеси и вытекающем потоке. Преобразовав уравнение (7.5),

можно без труда определить скорость образования компонента i, измерив его (стационарные) концентрации на входе в реактор и на выходе из него. Введенный в уравнение (7.6) параметр D называют скоростью разведения и определяют в виде

Этот параметр определяет время пребывания или скорость переработки в реакторе и равен числу объемов жидкой фазы реактора, проходящей через него в единицу времени. Параметр D представляет собой величину, обратную более обычным в химической технологии параметрам среднего времени пребывания или среднего времени удерживания. Здесь, однако, мы будем пользоваться общепринятым в литературе по биохимической технологии понятием о скорости разведения.

Из сравнения уравнений (7.3) и (7.6) нетрудно заметить, что кинетика процессов в ПРПП проще, чем в реакторе периодического действия; действительно, здесь нет необходимости в определении зависимости концентрации от времени и в последующем дифференцировании полученных данных. Изучение кинетики роста популяции клеток в этих условиях имеет еще одно преимущество, заключающееся в том, что в ПРПП клетки могут приспособиться к стационарным условиям и таким путем перейти в состояние сбалансированного или почти сбалансированного роста. Этим самым создается реальная возможность для обеспечения относительно определенного, воспроизводимого состояния клеточной популяции; в случае периодических процессов с участием микроорганизмов решить эту задачу значительно труднее. С другой стороны, эксперименты по изучению роста клеток в периодических процессах могут быть выполнены в небольших сосудах, размещенных на термостатированной качалке; оборудование для ПРПП значительно сложнее и дороже. Состояние стационарности в биологических ПРПП может быть достигнуто только через несколько часов или даже дней, что существенно повышает опасность внесения загрязнений, обесценивающих результаты эксперимента. Наконец, в крупномасштабном производстве в ряде случаев, вероятно, более целесообразными окажутся периодические процессы, отличающиеся непостоянным, несбалансированным ростом, различными метаболическими процессами и активностями в разные периоды процесса; для таких производств кинетические модели, основанные на стационарных условиях в ПРПП, могут оказаться вообще непригодными. Отсюда следует, что экспериментальному изучению кинетики роста популяций клеток микроорганизмов и высших организмов и разработке соответствующих математических выражений должно предшествовать точное определение предполагаемой сферы применения этих выражений. Это требование является основой для разработки программ экспериментального и математического моделирования.

В следующем разделе мы рассмотрим простейшие модели роста популяций клеток. При этом основное внимание мы будем уделять кинетике роста клеток в ПРПП, поскольку основные принципы построения кинетических уравнений были разработаны и наиболее полно развиты именно в экспериментах с хемостатами.

Кинетика сбалансированного роста

Моделирование и анализ кинетики роста популяций клеток мы начнем с неструктурированных моделей, в которых биофаза характеризуется только величиной клеточной массы или численной концентрацией. Суммарную скорость роста клеточной массы r_х часто выражают как µх, где х — клеточная масса в единице объема культуры, µ — удельная скорость роста клеток, выраженная в единицах обратного времени. В этих параметрах уравнение материального баланса клеточной массы для ПРПП в стационарном состоянии будет выглядеть следующим образом:

Часто поступающий в проточный реактор поток раствора питательных веществ состоит только из стерильного питательного вещества, так что X_f=0. В таком случае из уравнения (7.8) следует, что отличная от нуля популяция клеток может существовать в стационарном состоянии только при D=µ т. е. тогда, когда удельная скорость клеточного роста равна скорости разведения. Если выполняется условие уравнения (7.9), то при стерильном питательном веществе уравнение (7.8) уже не определяет х. Неопределенность уровня популяции была подтверждена в экспериментах с культурой Bacillus linens в проточном реакторе.

В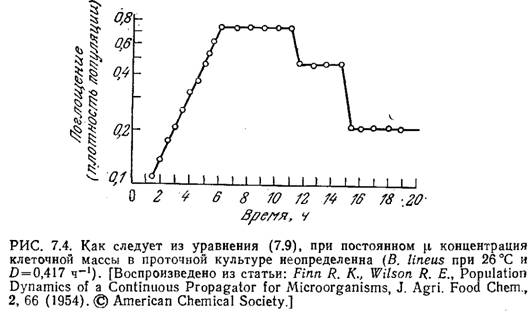 этих экспериментах стационарное состояние было достигнуто через 6 ч (рис. 7.4), после чего культуру подвергали двум последовательным разведениям, при которых часть содержимого реактора, состоящего из популяции клеток и среды, удаляли и замещали чистой средой. После каждого такого разведения через некоторое время в системе устанавливалось новое стационарное состояние, характеризующееся иной концентрацией клеточной массы.

Уравнение Моно для кинетики клеточного роста

Приведенная на рис. 7.4 зависимость характерна только для тех случаев, когда удельная скорость клеточного роста не зависит от х и s. [Здесь под s мы понимаем массовую концентрацию субстрата, лимитирующего клеточный рост.] Система становится определенной, если скорость роста клеток лимитируется каким-либо питательным веществом.

Прежде чем перейти к обсуждению деталей зависимости скорости роста от подачи питательных веществ, рассмотрим общие теоретические и практические пути создания сред для культивирования клеток.

В зависимости от состава различают два типа сред. Синтетическими называют среды с четко определенным химическим составом. Как показано в табл. 7.1, такие среды создаются на основе раствора неорганических солей, к которому добавляют необходимые источники углерода, азота и энергии, а также все незаменимые витамины. Неорганические соли служат не только источником ионов, необходимых для нормального функционирования клеток, но и выполняют буферную функцию, сглаживая большие флуктуации рН в процессе роста популяций. Сложные среды содержат материалы неопределенного состава. Например, среда 4 в табл. 7.1 относится к сложным, поскольку точный химический состав дрожжевого экстракта неизвестен. В состав других сложных сред входят мясной бульон, кровяной бульон, кукурузный экстракт и сточные воды.

Основное требование, предъявляемое к среде, заключается в обеспечении высокой скорости роста клеток и(или) синтеза продуктов их жизнедеятельности.

Отсюда, однако, отнюдь не следует (как можно было бы предположить чисто интуитивно), что все питательные вещества нужно подавать в большом избытке. Во-первых, избыточная концентрация питательного вещества может ингибировать рост клеток или даже привести к их гибели. Во-вторых, если клетки растут слишком интенсивно, то накапливающиеся конечные продукты метаболизма могут нарушить нормальные биохимические процессы в клетках. Поэтому обычно общий рост клеток лимитируют, ограничивая количество одного питательного вещества в среде.

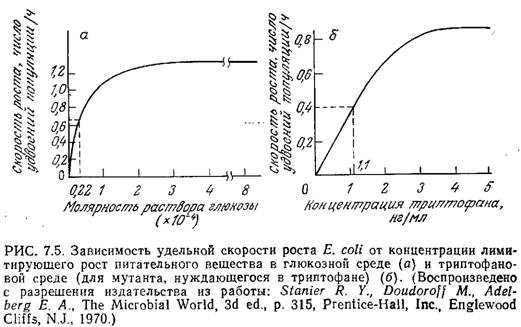
Если концентрация одного незаменимого компонента среды изменяется, а концентрации всех других компонентов остаются без изменения, то, как это показано на рис. 7.5, зависимость скорости клеточного роста от концентрации незаменимого питательного вещества обычно выражается кривой типа гиперболы. Математическое выражение, отражающее функциональную зависимость удельной скорости клеточного роста р, от концентрации незаменимого питательного вещества, было предложено Моно в 1942 г. Уравнение Моно имеет ту же форму, что и уравнение изотермы адсорбции Ленгмюра (1918 г.) и обычное уравнение скорости катализируемой ферментом реакции с одним субстратом, предложенное Анри (1902 г.) и Михаэлисом. и Ментен (1913 г.), и устанавливает, что

В этом уравнении µ_max — максимальная скорость роста, достигаемая при s>Ks и постоянных концентрациях всех других незаменимых питательных веществ. Ks — это такая концентрация лимитирующего клеточный рост питательного вещества, при которой удельная скорость роста вдвое ниже максимального значения. В первом приближении можно считать, что Ks представляет собой промежуточную зону между диапазоном низких концентраций, при которых µ линейно зависит от s, и диапазоном высоких концентраций, когда µ становится независимым от s. Как показано на рис. 7.5, значения Ks для штаммов Е. coli, растущих в лимитируемых глюкозой и триптофаном средах, составляют 0,22-10^-4 М и 1,1 нг/мл соответственно.

Поскольку мы уже знакомы с биохимией клетки, для нас должно быть очевидно, что уравнение Моно, скорее всего, чрезмерно упрощено. Как, однако, это часто бывает и в других областях технологии, относительно простое уравнение иногда удовлетворительно описывает определенные зависимости, хотя физический смысл параметров модели неизвестен или, возможно, даже, вообще не существует. Впрочем, в некоторых специфических ситуациях уравнению Моно можно приписать определенный физический смысл. Одна из наиболее показательных ситуаций такого типа складывается тогда, когда скорость клеточного роста лимитируется скоростью транспорта через мембрану при участии пермеаз (вспомните разд. 5.7).

В уравнении Моно (7.10) привлекает его простота, однако применение этого простого выражения требует от исследователя большой осторожности. Во-первых, величина Ks часто довольно мала, поэтому s обычно намного больше Ks и выражение s/(Ks + s) можно рассматривать как адекватное выражению для расчета отклонений µ от µ_mах по мере снижения концентрации s. Это соотношение предполагает также, что удельная скорость роста р, не равна нулю при любых отличных от нуля концентрациях лимитирующего скорость клеточного роста компонента. В общем случае данное условие нельзя считать доказанным для s<Ks.

Если скорость роста популяции клеток связана с концентрацией лимитирующего клеточный рост питательного вещества математическим выражением типа уравнения Моно, то отсюда следует, что между условиями работы реактора и кинетическими и стехиометрическими параметрами популяции клеток должны существовать определенные зависимости. Для выявления этих зависимостей можно начать с уравнения материального баланса по лимитирующему клеточный рост субстрату, связанного с балансом по, клеточной массе, поскольку ц зависит от s. В балансе по субстрату мы будем использовать экономический коэффициент Ух/s (см. разд. 5.10.1):

Уравнения (7.14) и (7.15) отражают зависимость х и s от скорости потока (D = F/V) в стационарном состоянии. Для очень медленных скоростей потока при заданном объеме, следовательно, s также приближается к нулю. Поскольку почти весь вводимый в реактор субстрат поглощается клетками, то концентрация клеточной массы на выходе из реакторах х будет равна S_fY_x/s.

По мере постепенного повышения D возрастает и s: сначала пропорционально D, а затем, по мере приближения D к µ_mах, еще быстрее. Точно таким же образом снижается и концентрация клеточной массы — сначала в линейной зависимости от D, а затем, при D→ µ_mах, с большей скоростью. При приближении D к µ_mах в какой-то момент х становится равной нулю; это означает, что скорость разведения D только что превысила максимально возможную скорость роста и решение уравнения (7.14) в условиях стационарного состояния возможно только при х = 0.

Потеря всех клеток в стационарном состоянии, называемая вымыванием, происходит, когда D больше D_mаx; последний параметр можно определить по уравнению (7.14) при х = 0:

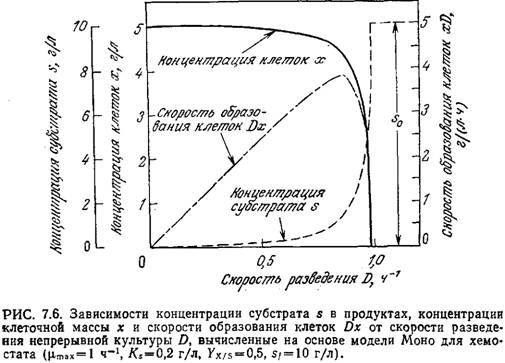
На рис. 7.6 приведены отражаемые уравнениями (7.14) и (7.15) графики зависимостей концентраций субстрата и клеточной массы от D для следующего ряда значений параметров:

µ_mах =1,0ч^-1 У_х/s = 0,5 Кs=0,2г/л s_f=10 г/л

Заметьте, что вблизи точки вымывания реакционная смесь становится очень чувствительной к колебаниям D; даже небольшое изменение D сопровождается относительно большим изменением х и (или) s.

Эту зависимость необходимо иметь в виду в тех случаях, когда целью непрерывного микробиологического процесса является производство биомассы. Скорость продуцирования клеток в единице объема реактора равна Dx; на кривой зависимости Dx от D (рис. 7.6) имеется резкий максимум. Максимальную скорость образования клеток можно вычислить, решив дифференциальное уравнение

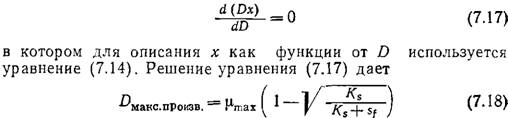
Если, как это часто бывает на практике, S_f>K_s, то D макс.произв. приближается к µ_mах и, следовательно, находится вблизи точки вымывания. В такой ситуации, изображенной, в частности, на рис. 7.6, как правило, чтобы избежать диапазона наибольшей чувствительности, целесообразно не добиваться максимальной скорости образования биомассы. Вообще при решении любых проблем оптимизации в поисках сравнительно легко регулируемых параметров важно не забывать практические аспекты сочетания чувствительности, регулируемости и надежности.

При изучении закономерностей образования конечных продуктов непрерывных микробиологических процессов введем еще один коэффициент Y_р/х, представляющий собой отношение

Вместе с приведенными выше уравнениями, выражающими зависимость |µ и х от параметров процесса, уравнение (7.21) позволяет вычислить концентрацию продукта в выходящем из реактора потоке. Производительность реактора по отношению к продукту равна pD и при постоянном Y_p/х максимальна, если D имеет значение, определяемое уравнением (7.18). Следовательно, при попытках добиться максимальной производительности процесса также необходимо учитывать фактор чувствительности. [При каком значении D величина pD максимальна, если Y_P/x = f (D) ?]

В качестве примера на рис. 7.7 приведены результаты экспериментального изучения роста культуры бактерий Aerobacter aerogenes в проточном реакторе. Экспериментальные результаты и описанная выше простая математическая модель качественно вполне согласуются. В то же время найденная скорость образования клеточной массы и найденная концентрация субстрата остаются приблизительно постоянными в значительно более широком диапазоне условий, чем следует из рассчитанных по уравнению Моно данных (рис. 7.6). Кроме того, модель Моно не согласуется с экспериментальными данными при очень низких и очень высоких скоростях разведения.

В следующем разделе мы изучим эти две экстремальные ситуации и попытаемся понять, почему в таких случаях модель Моно неприменима.

Влияние эндогенного метаболизма и метаболизма поддержания на кинетику клеточного роста

Приведенные на рис. 7.8 данные для культуры А. aerogenes показывают, что при малых скоростях разведения концентрация клеток заметно снижается. Аналогичное поведение наблюдалось и в случае кормовых дрожжей Toruta utilis. Эту особенность, противоречащую модели Моно для хемостата, можно объяснить, если в модели учесть возможность эндогенного метаболизма.

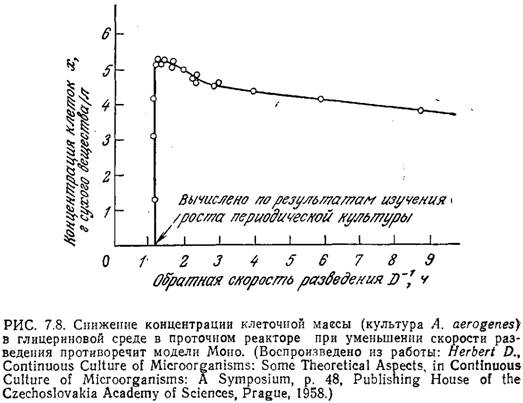
Под эндогенным метаболизмом подразумеваются происходящие в клетке реакции, в которых расходуются клеточные вещества. Чтобы учесть этот эффект, дополним уравнение Моно слагаемым —k_ex:

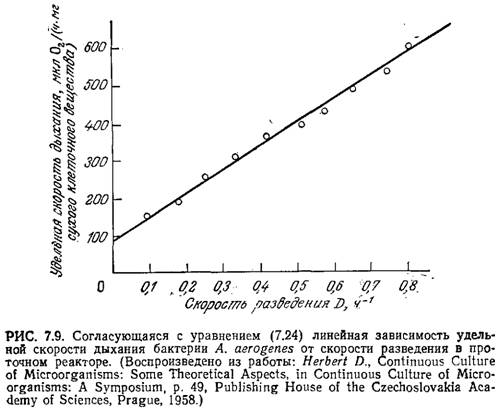
Приведенные на рис. 7.9 экспериментальные данные хорошо согласуются с уравнением (7.24).

Наблюдаемая зависимость экономического коэффициента У от D также подтверждает справедливость уравнения (7.22) для скорости клеточного роста. Если скорость поглощения субстрата равна

Экспериментально показано, что для ряда микроорганизмов зависимость Y_x/s от D выражается именно таким уравнением.

Другая возможность, рассмотренная вкратце при обсуждении стехиометрии клеточного роста в разд. 5.10.1, заключается в параллельной утилизации субстрата как для клеточного роста, так и для других энергетических потребностей клетки (метаболизм поддержания). В этом случае скорость утилизации субстрата определяется выражением

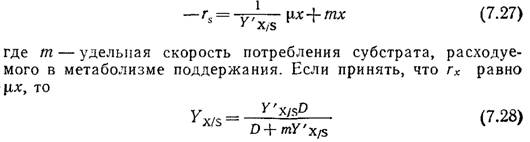
Таким образом, мы получили точно такую же функциональную зависимость Yx/s от D, как и в случае модели эндогенного метаболизма [уравнение (7.26)].

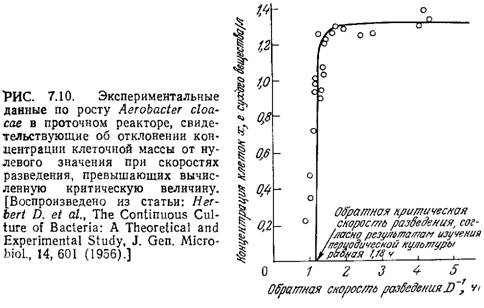
Как показано на рис. 7.10, при высоких скоростях разведения поведение культуры клеток в проточном реакторе может существенно отклоняться от поведения, предсказываемого моделью Моно для хемостата. Здесь не только слишком велика ошибка в определении концентрации клеток вблизи точки вымывания, но и вся популяция клеток может существовать при скоростях разведения, значительно превышающих предсказываемую теорией критическую величину. Более того, по мере приближения D к критическому максимальному значению экономический коэффициент снижается. Одна из возможных причин этого несоответствия может заключаться в относительно высокой концентрации субстрата, характерной для высоких скоростей разведения. В таких условиях субстрат часто не ограничивает рост клеток, и составляющие популяцию клетки могут изменить характер метаболизма, выбрав какой-либо другой лимитирующий фактор среды.

Влияние других параметров среды на кинетику клеточного роста

При сбалансированном росте для характеристики кинетики роста популяции клеток достаточно только одного параметра д. (или времени удвоения численности популяции t_d = ln2/µ). По этой причине параметр удельной скорости роста д. широко используется для описания влияния среды на поведение популяции. Рассмотрим прежде всего влияние температуры; известно, что живые организмы могут существовать в диапазоне температур примерно от -5 до 95 °С Принято классифицировать прокариоты в соответствии с диапазоном температур их роста. Как показывают приведенные в табл. 7.2 данные, для каждого класса микроорганизмов характерна некоторая оптимальная температура, при которой скорость роста достигает максимума, а также верхняя и нижняя температурные границы, вне которых популяция вообще не способна к росту.

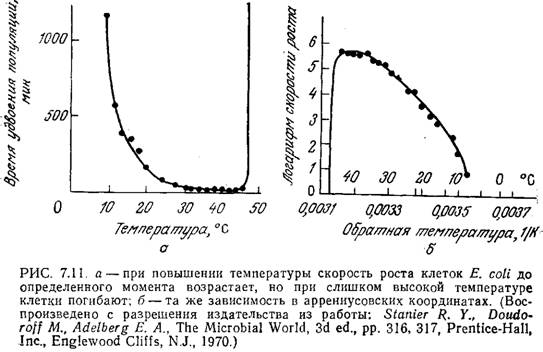
Приведенные на рис. 7.11 кривые свидетельствуют об очень сильном влиянии температуры на рост Е. coli. Обратите внимание на то, что в координатах Аррениуса классическое аррениусовское поведение наблюдается только при низких температурах, а по мере приближения температуры к той границе, при которой бактерии начинают погибать, скорость их роста резко падает. Бросается в глаза сходство зависимостей клеточного роста (рис. 7.11) и каталитической активности ферментов (рис. 3.25) от температуры.

В этой связи неудивительно, что зависимость удельной скорости клеточного роста от температуры часто можно выразить в виде уравнения типа (3.73). Очевидно, в диапазоне относительно низких температур возрастание метаболической активности клетки при повышении температуры связано с повышением каталитической активности входящих в ее состав ферментов. Когда же температура достигает того предела, при котором начинается денатурация термически наиболее лабильных важных для жизнедеятельности клетки белков, то клетка погибает. В ряде случаев эта гипотеза была подтверждена генетическими методами; показано» в частности, что мутация одного гена может существенно изменить максимальную температуру, которую способен выдержать микроорганизм.

Поскольку конформация белка и его активность зависят от рН, мы вправе ожидать, что величина рН будет оказывать существенное влияние на процессы клеточного транспорта, скорости реакций, а следовательно, и скорость роста клеток. Обычно скорость роста бактерий максимальна в диапазоне pFi от 6,5 до 7,5. В качестве примера на рис. 7.12 приведена зависимость скорости роста Е. coli от рН.

Впрочем, из этого правила есть и исключения. Так, ацидофильные бактерии растут при рН 2,0. Обычно отклонение рН на 1,5—2 единицы в любую сторону от оптимальной величины приводит к практически полному прекращению роста (рис. 7.12). Дрожжи лучше всего растут в диапазоне рН от 4 до 5, а оптимальный рН для роста плесневых грибов обычно равен 5—7. Для дрожжей и плесеней характерен довольно широкий диапазон роста — приблизительно от рН 3,0 до рН 8,5. Как показывают приведенные на рис. 7.12 данные, при повышении температуры рН максимальной скорости клеточного роста обычно возрастает.

Н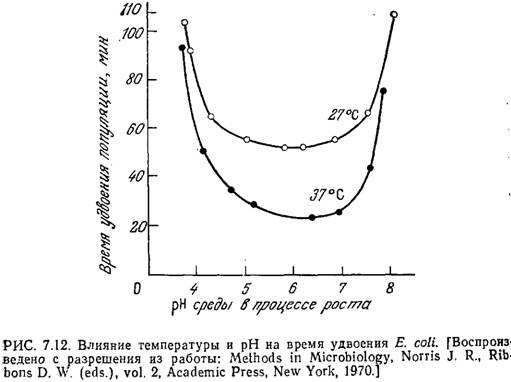 а удельную скорость роста микроорганизмов влияют также термодинамическая активность среды (зависящая в свою очередь от растворенных в ней веществ) и гидростатическое давление. Скорость роста аэробных организмов, очевидно, в существенной степени зависит от концентрации растворенного кислорода.

Кинетика клеточного роста в переходном состоянии

В определенные периоды роста культур клеток в реакторах периодического действия или после возмущений в проточных реакторах непрерывного действия популяции клеток находятся в переходном состоянии, кинетика которого может оказаться весьма сложной. Для описания различных вариантов роста клеток в переходном состоянии могут потребоваться разные типы математических моделей кинетики роста. Здесь мы рассмотрим несколько примеров кинетики клеточного роста в переходном состоянии, причем основное внимание уделим наиболее общему случаю роста популяции в реакторе периодического действия.

Основные фазы роста клеток в реакторах периодического действия

К ак показано на рис. 7.13, в типичном периодическом процессе число живых клеток изменяется во времени. После лагфазы (фазы задержки, латентной фазы), в течение которой численность популяции практически не изменяется, наступает период быстрого роста, когда число клеток возрастает во времени экспоненциально. Часто эту стадию роста культур клеток в реакторе периодического действия называют логарифмической фазой (лаг-фазой); мы предпочитаем более точный термин - экспоненциальный рост, который и будем использовать в последующем изложении.

Понятно, что в закрытом сосуде клетки не могут размножаться бесконечно, и вслед за фазой экспоненциального роста наступает стационарная фаза. В этот момент число клеток достигает максимума. В конце концов стационарная фаза сменяется фазой отмирания, когда число клеток начинает снижаться. Здесь также часто наблюдается экспоненциальное снижение, численности популяции живых организмов.

В микробиологических процессах важную роль может играть любая из фаз. Так, при разработке процесса одной из его задач может быть сокращение до минимума продолжительности лаг-фазы и достижение максимальной длительности фазы экспоненциального роста (и скорости роста клеток в этой фазе); вторая цель в свою очередь достигается путем искусственного торможения перехода к стационарной фазе. Часто очень важно к концу процесса добиться максимальной плотности популяции клеток, что возможно только при условии учета всех переменных, влияющих на фазы роста культуры. В последующем изложении мы будем рассматривать каждую фазу отдельно и в соответствующие моменты обсудим математические модели наиболее важных явлений. Это обсуждение мы продолжим в разд. 7.3.2, где рассмотрим математические модели всего процесса клеточного роста в реакторе периодического действия.

Продолжительность лагфазы, наступающей после инокуляции свежей среды, зависит как от изменений в составе питательных веществ (если такие изменения имеют место), так и от возраста и массы инокулята. Сопровождающее перенос клеток из одной среды в другую резкое изменение условий может оказывать на живые клетки разностороннее действие. Во-первых, как мы уже знаем, системы контроля и регуляции ферментативной активности включают и адаптационные механизмы; в частности, сталкиваясь с новым питательным веществом, клетка начинает его усваивать только после синтеза новых ферментов. Поэтому, например, перенос находящейся в экспоненциальной фазе культуры из глюкозной среды в лактозную всегда сопровождается периодом с незначительной скоростью деления клеток; в этот период в клетках синтезируются ферменты и кофакторы, участвующие в пути метаболизма лактозы. (Что произойдет, если выращенную на лактозе культуру перенести в глюкозо-лактозную среду) Аналогично лаг-фаза может наступить и после изменения концентраций питательных веществ. Если новая питательная среда богаче лимитирующим клеточный рост питательным веществом, то в течение некоторого времени это вещество будет расходоваться не на рост клеток, а на повышение концентраций метаболизирующих ферментов. Снижение концентрации питательного вещества может и не сопровождаться лаг-фазой; в этом случае экспоненциальный рост возобновляется сразу же после снижения концентрации, но скорость клеточного роста снижается.

Для активации многих внутриклеточных ферментов необходимы те или иные низкомолекулярные соединения (витамины, кофакторы) или ионы металлов (активаторы), которые могут проникать через клеточные мембраны. Перенос небольшого объема культуры клеток или инокулята в значительно больший объем среды вызовет обратную диффузию этих необходимых для ферментативного катализа веществ в среду, если в последней они отсутствуют или если среда резко отличается от инокулята по своей ионной силе. В таком случае опять-таки скорость роста упадет соответственно понижению концентрации активаторов в клетке, что в свою очередь, повлечет за собой лаг-фазу на период «включения» новых механизмов синтеза этих активаторов. Если в описанных процессах снижаются концентрации незаменимых активаторов (ионов и витаминов, которые не могут синтезироваться в клетке), то общий уровень клеточной активности должен снизиться необратимо.

На длительность лаг-фазы очень большое влияние оказывает фаза роста, в которой находится инокулят, полученный в свою очередь путем культивирования клеток в небольшом реакторе периодического действия. Объем инокулята также является важной переменной; в частности, как мы уже упоминали, она влияет на количество диффундирующих в среду веществ, например витаминов и активаторов. Так, перенос популяции молодых клеток в среду, богатую промежуточными метаболитами (например, аминокислотами), не сопровождается лаг-фазой; напротив, при переносе того же самого инокулята в среду с сульфатом аммония клетки будут обедняться жизненно важными промежуточными веществами за счет их транспорта в раствор. Если в момент переноса культура находится в фазе экспоненциального роста, то в среде инокулята уже должны содержаться в значительных концентрациях продукты промежуточного метаболизма, поэтому сопровождающее перенос разведение окажет меньший эффект.

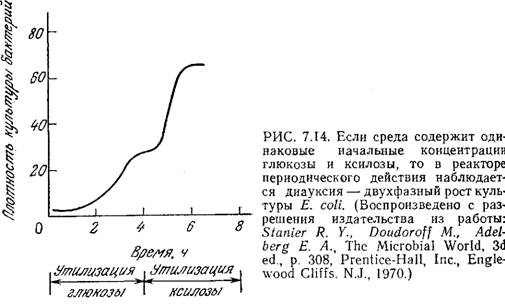
Перенос в аммониево-сульфатную среду старой культуры (находящейся в стационарной фазе или близкой к ней) приведет к более длительной лаг-фазе. Если среда содержит несколько источников углерода, то иногда можно наблюдать ряд последовательных лаг-фаз (рис. 7.14). Это явление, называемое диауксией (двухфазным ростом), обусловливается изменением метаболического механизма в процессе роста. При диауксии клетки сначала усваивают один источник углерода, а затем, когда это питательное вещество истощается, клеткам приходится переключать свою активность с роста на «перестройку», необходимую для усвоения нового источника углерода. В основе такой последовательной утилизации питательных веществ, возможно, лежит явление катаболитной репрессии, рассмотренное в разд. 6.1.4.

Попытки свести к минимуму время роста культуры и всего процесса обычно включали сокращение продолжительности лаг-фазы, типичной для любого периодического процесса с участием микроорганизмов. Из уже рассмотренного нами материала и ряда других данных (описанных в приведенной в конце главы литературе) вытекают следующие общие принципы:

1. Культура инокулята должна обладать максимальной активностью, а в момент введения в среду инокулят должен находиться в фазе экспоненциального роста.

2. Среда, в которой выращивается инокулят, по своему составу должна быть близкой к составу среды крупномасштабного микробиологического процесса.

3. Для предотвращения обусловленных диффузией потерь незаменимых промежуточных веществ и активаторов целесообразно применять инокулят большего объема (до 5—10% от объема новой среды).

К концу лаг-фазы популяция микроорганизмов приспосабливается к новым условиям. Теперь клетки могут быстро размножаться, и клеточная масса (или число живых клеток) удваивается через определенные промежутки времени. Увеличение числа клеток в этот период может быть описано уравнением

Как и в случае роста клеток в стационарном состоянии в ПРПП, для описания популяции в ходе экспоненциального роста в периодическом процессе необходим только один параметр µ (или td). В первом приближении можно считать, что в этой фазе рост периодической культуры сбалансирован. Следовательно, путем изучения роста культуры клеток в реакторе периодического действия можно получить полезные данные о кинетике сбалансированного роста, если только это изучение ограничено фазой экспоненциального роста.

Экспоненциальный рост заканчивается, когда одна из важных переменных процесса (например, концентрация питательного вещества или токсина) достигает значения, не обеспечивающего максимальную скорость роста клеток. Истощение запасов лимитирующего рост питательного вещества может привести к очень резкому изменению скорости клеточного роста, поскольку в экспоненциальной фазе общая скорость утилизации питательного вещества возрастает очень быстро. Чтобы найти описывающее это явление приближенное математическое выражение, предположим, что до установления стационарной фазы скорость потребления питательного вещества А пропорциональна массовой концентрации живых клеток:

Допустим далее, что экспоненциальный рост продолжается до тех пор, пока не установится стационарная фаза, и что экспоненциальный рост начинается в нулевой момент времени. Тогда

где хо — массовая концентрация живых клеток в момент начала экспоненциального роста.

Если в нулевой момент времени концентрация А равна a_о, то из уравнений (7.38) и (7.39) следует, что А будет полностью утилизировано, когда

Здесь x_s—массовая концентрация популяции в тот момент, когда вещество А истощено и популяция переходит в стационарную фазу.

Следовательно, x_s представляет собой максимальную концентрацию биомассы в периодическом процессе (ср. рис. 7.13). Преобразованием уравнения (7.40) можно получить уравнение, выражающее максимальную концентрацию биомассы в момент истощения питательного вещества:

Линейная зависимость x_s от начальной концентрации питательного вещества а_о во многих случаях наблюдалась экспериментально (x₀ часто настолько мало, что им можно пренебречь). Пример такого поведения популяции клеток приведен на рис. 7.15. В то же время график зависимости n_s (численной плотности клеток в стационарной фазе) бактерии A. aerogenes от концентрации лактозы заметно отличается от зависимости, предсказываемой уравнением (7.41).

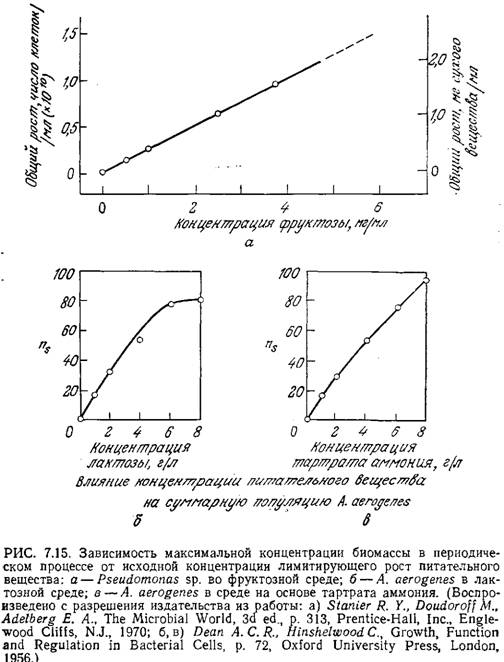
Очевидно, на начало стационарной фазы и максимальную концентрацию биомассы могут влиять и другие факторы.

Согласно уравнению (7.42), рост клеток прекращается только тогда, когда c_t достигает значения, равного 1/b. Разведение данной среды, содержащей токсин, или введение непитательного вещества, связывающего этот токсин, должно сопровождаться возобновлением клеточного роста и, следовательно, увеличением максимальной концентрации биомассы xs в стационарной фазе. Если рост сдерживается истощением питательного вещества, то разведение раствором, не содержащим питательных веществ, не влияет на x_s. Этими зависимостями можно пользоваться в качестве критериев для предварительной оценки причин снижения скорости и прекращения клеточного роста. Более точные критерии сформулировать труднее, поскольку, как мы увидим позднее, рост популяции клеток в условиях истощения основного питательного вещества замедляется несколько раньше, чем это вещество полностью утилизируется, а скорость роста клеток в присутствии токсина может стать неизмеримо малой задолго до того момента, когда dx/dt станет равным нулю.

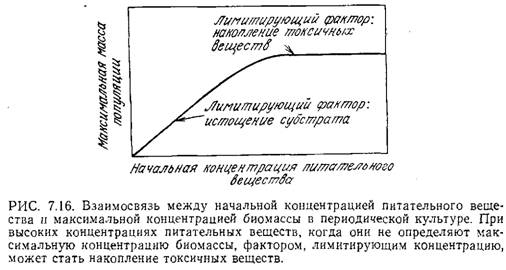
На рис. 7.16 изображена предсказываемая теорией зависимость максимальной концентрации биомассы от исходной концентрации данного питательного вещества.

Постепенное снижение концентрации питательного вещества в конце концов приводит к линейной зависимости максимальной концентрации биомассы от начальной концентрации питательного вещества. В этом случае отсутствие фазы экспоненциального роста, очевидно, вызвано недостатком питательного вещества. Напротив, повышение начальной концентрации питательного вещества может привести к тому, что величина x_s в конце концов перестанет быть зависимой от а₀; возможно, это объясняется накоплением токсичных веществ или влиянием другого лимитирующего клеточный рост питательного вещества.

Изучая всю популяцию, мы не должны забывать о судьбе индивидуальных клеток. В общем случае популяции всегда негомогенны, и кривая роста популяции в периодическом процессе отражает лишь некоторый усредненный параметр чрезвычайно сложной системы. Во время фазы экспоненциального роста, например, некоторые клетки делятся и порождают новые, молодые клетки, а другие в тот же самый момент растут и созревают. Поскольку клетки разного возраста обычно имеют различные размеры и химический состав, мы можем рассматривать клетки одного возраста как некоторое «вещество». С этой точки зрения рост одного вида микроорганизма приводит к популяции, содержащей множество различных «веществ».

Гетерогенность популяции становится особенно заметной в стационарной фазе и фазе отмирания. Так, в стационарной фазе некоторые клетки делятся, а некоторые погибают. Мертвые клетки часто подвергаются лизису (разрушению и растворению); в результате углеводы, аминокислоты и другие компоненты клеток попадают в среду и становятся питательными веществами для живых членов популяции. Такой каннибализм способствует сохранению массы популяции в стационарной фазе. В конце концов, однако, истощение питательных веществ и накопление токсинов приводит к тому, что популяция не может поддерживать далее свое существование и наступает фаза отмирания.

Фазе отмирания было посвящено сравнительно небольшое число исследований, возможно, вследствие того, что многие промышленные микробиологические периодические процессы заканчиваются задолго до наступления этой фазы. Обычно считается, что гибель популяции подчиняется экспоненциальному закону: х=х_se^-kt (7.48)

В этом уравнении t означает время, прошедшее с начала фазы отмирания

В основу уравнения (7.48) положено допущение о том, что в любое время погибает одна и та же доля живых клеток.

Одно из объяснений экспоненциального уменьшения численности популяции в фазе отмирания заключается в том, что в культуре клеток летальный исход является случайным событием и гибель данной клетки определяется только вероятностью этого события. Недостатком такого объяснения является пренебрежение историей популяции. Дин и Хиншелвуд предположили, что в стабильной и отмирающей популяциях не только живые клетки существуют за счет отмерших, но и конкурирующие участки метаболического механизма клетки в борьбе за дефицитные промежуточные соединения также существуют один за счет другого [3]. Если принять это предположение, можно показать, что скорость гибели клеток должна подчиняться экспоненциальному закону. Другие модели снижения численности популяции мы обсудим в разд. 7.7.

Чтобы лучше понять закономерности роста популяции клеток в периодическом процессе и создать основу для вывода соответствующих математических выражений, целесообразно, рассмотреть ряд результатов экспериментального изучения изменений массы и химического состава популяции в периодических процессах. Следует опять-таки подчеркнуть, что эти результаты относятся не к индивидуальной клетке, а к совокупности множества клеток, составляющих популяцию в данный момент.

Дин, Хиншелвуд и другие исследователи посвятили много работ изучению изменений в составе культуры бактерий A. aerogenes. В частности, ими было показано, что в среде, содержащей глюкозу, лаг-фаза сокращается до минимума, если инокулят взят из популяции в стационарной фазе, наступившей после истощения запасов глюкозы. Полученные данные изображены на рис. 7.17. Обратите внимание на то, что на ранних этапах цикла роста на кривых изменения средней массы клетки и отношения РНК/ДНК наблюдаются резкие максимумы. Хотя количество ДНК в расчете на единицу клеточной массы и отношение массы белков к массе РНК остаются относительно постоянными, по этим данным в совокупности с некоторой другой информацией нетрудно воспроизвести картину активизации метаболической активности клетки, направленной на использование повышенных количеств питательных веществ в новой среде и на синтез больших количеств диффундирующих промежуточных метаболитов.

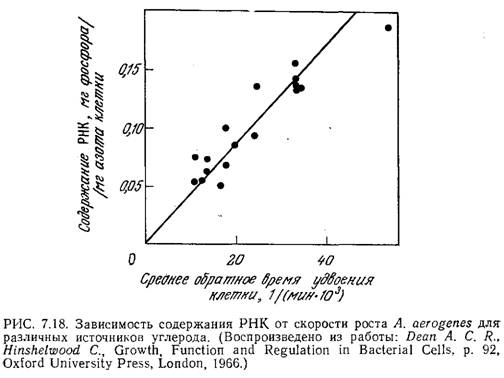
На рис. 7.18 представлены данные, иллюстрирующие другое интересное явление, к которому мы обратимся еще раз при изучении скоростей образования конечных продуктов жизнедеятельности клеток. Средняя концентрация РНК в клетке возрастает пропорционально скорости роста популяции. Следует подчеркнуть, что такая зависимость наблюдается только тогда, когда изменение скорости роста обусловлено вариациями в составе питательной среды. Если же скорость клеточного роста изменяется, например, за счет понижения или повышения температуры, то в фазе экспоненциального роста концентрация РНК, по-видимому, остается практически на одном уровне.

В завершение этого раздела мы несколько подробнее рассмотрим свойства популяций клеток и характер изменения активностей ферментов в течение клеточного цикла. В фазе экспоненциального роста A. aerogenes концентрации двух ферментов с гидрогеназной активностью изменяются очень мало, в то время как удельная активность аспарагиндеаминазы варьирует в довольно широких пределах. Первоначальное падение активности этого фермента приписывается разбавлению инокулята, а повышение активности в конце клеточного цикла обусловлено, по-видимому, снижением рН среды на этой стадии процесса.

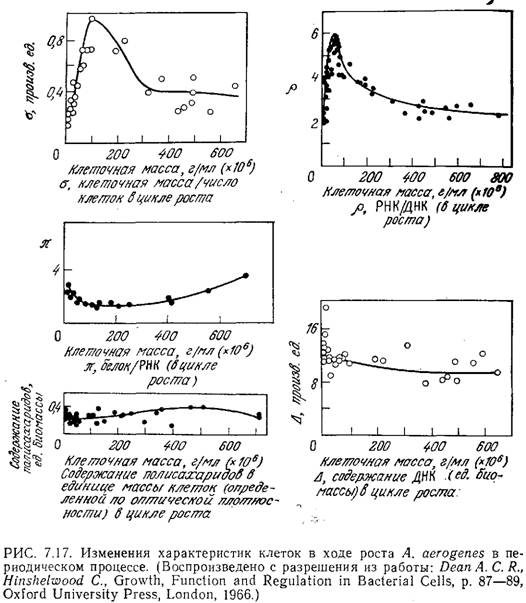
Этот факт лишний раз свидетельствует о том, что периодическую культуру клеток следует рассматривать как сложную единую систему, состоящую из популяции клеток и жидкой среды переменного состава. В известном смысле рост популяции в периодическом процессе можно считать функцией начальных характеристик не только клеток, но и среды, поэтому любые параметры популяции после начала процесса зависят от каждой из этих двух фаз. Таким образом, в общем случае до известной степени необоснованно рассматривать свойства одной лишь популяции клеток в периодическом процессе роста, поскольку эти свойства определяются взаимодействием между средой и популяцией.

Неструктурированные модели клеточного роста в периодических процессах

В простейшем подходе к моделированию роста культуры клеток в периодическом процессе мы допускаем, что скорость роста клеточной массы во времени является функцией одной лишь клеточной массы, т. е.

Как мы скоро увидим, из этого уравнения отнюдь не следует, что мы должны пренебрегать любыми изменениями, происходящими в ходе клеточного роста в среде.

Одной из простейших моделей типа (7.49) является закон Мальтуса, который математически можно выразить следующим образом:

где µ — константа. Нетрудно видеть, что таким же образом выражается уже известная нам закономерность накопления клеточной массы в фазе экспоненциального роста. Предсказание Мальтуса о неизбежности рокового конца человечества в результате неконтролируемого роста народонаселения не оправдалось (или, быть может, пока еще не оправдалось?); так же и в случае популяций микроорганизмов вслед за фазой экспоненциального роста наблюдается переход к стационарной популяции.

Эта теория получила дальнейшее развитие в работах Ферлхурста (1844 г.), а также Перла и Рида (1920 г.), которые при анализе роста популяции стали учитывать ингибирующий фактор. Допустив, что ингибирование пропорционально х², эти исследователи предложили уравнение

Это выражение представляет собой уравнение Риккати; его интегрирование не представляет затруднений и приводит к уравнению логистической кривой:

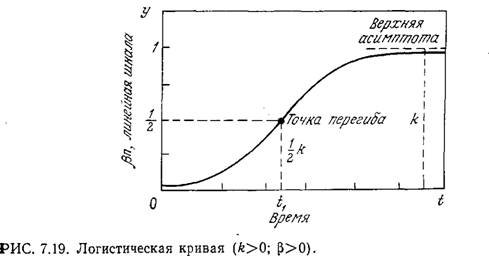
Как показано на рис. 7.19, логистическая кривая имеет S-образную форму и приводит к стационарной популяции с максимальной концентрацией биомассы x_s=l/β.

Одно из возможных объяснений логистической кривой сводится к допущению, что скорость продуцирования токсина пропорциональна скорости роста популяции:

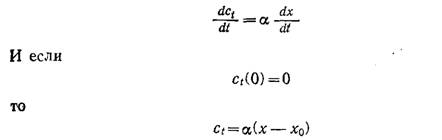
Обычно пренебрежимо мало по сравнению с x; в таких случаях подстановка уравнения (7.55) в (7.42) приводит к уравнению типа (7.51).

В основу неструктурированных моделей другого типа, описывающих приближающиеся к стационарному состоянию популяции, положен принцип истощения лимитирующего рост питательного вещества. Если, как и при выводе уравнения Моно, допустить, что µ=µ(s) и что общий экономический коэффициент Y_x/s постоянен, то уравнения материального баланса для питательного вещества и клеточных веществ можно объединить в одном уравнении типа (7.49) (см. упражнение 7.14).

Недостатком логистического уравнения является пренебрежение фазой снижения массы (численности) популяции после того, как стационарная популяция исчерпала все свои ресурсы. Этот фактор учтен в модели, разработанной в начале этого столетия Вольтеррой. В модели Вольтерры уравнение (7.50) дополняется интегральным членом типа

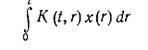
Физический смысл выражения (7.56) в первом приближении можно интерпретировать как влияние истории популяции K(t,r) на скорость ее роста. Выражение (7.56) отражает зависимость скорости роста во время t от всех предыдущих значений плотности популяции. Если К не зависит от t, то выраже­ние (7.56) можно рассматривать как отражение влияния компонента культуры, изменение концентрации которого подчиняется закону

Предположим, что К постоянно и равно Ко, и дополним уравнение (7.51) выражением (7.57), отражающим предыдущую историю популяции. Тогда изменение массы или плотности

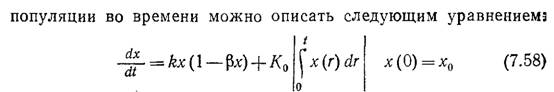
В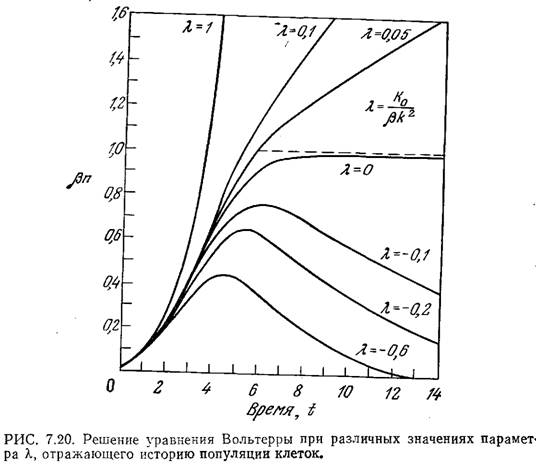 соответствии с уравнением (7.58) Ко для ингибитора имеет отрицательное значение, а для соединения, промотирующего клеточный рост, — положительное. Это уравнение можно решить численно; пример такого решения приведен на рис. 7.20. При отрицательных Ко масса популяции достигает максимума и затем уменьшается.

Описанные выше неструктурированные модели клеточного роста имеют несколько недостатков. В частности, в них не находит отражения лаг-фаза, не учтены влияющие на рост клеток различные переменные, а также данные о метаболизме клетки и его регуляции. В последующих разделах мы попытаемся найти связи между сложной биохимией клетки и явлениями, наблюдаемыми при росте популяции в периодическом процессе.

Рост филаментозных организмов

В предыдущих разделах настоящей главы мы рассматривали популяции микроорганизмов, в которых увеличение биомассы сопровождается повышением числа клеток. По-другому складывается ситуация при росте плесневых грибов и других филаментозных организмов; здесь по мере роста культуры изменяется как масса, так и морфология гранул или суспензии плесени. Экспериментальное изучение роста погруженных культур в периодических процессах показало, что количество биомассы возрастает во времени не экспоненциально, а с меньшей скоростью, так что масса популяции приблизительно пропорциональна третьей степени времени. Чтобы объяснить эту зависимость, нужно начать изучение с одно- и двумерных культур плесневых грибов. В случае одномерной культуры скорость увеличения длины колонии остается постоянной во времени, а для культур плесеней на поверхности (двумерных) характерна постоянная скорость увеличения радиуса культуры.

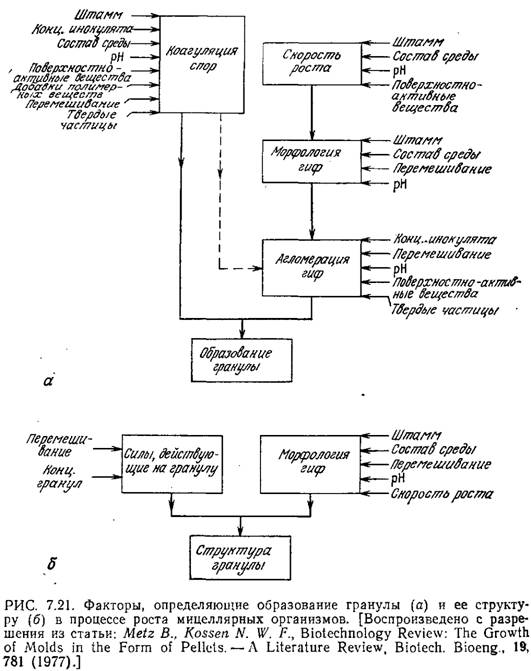
Полный анализ роста филаментозного организма должен учитывать также кинетику образования гранул. Последние возникают в результате агломерации спор и последующего роста или в результате разрастания отдельной споры. Имеющиеся данные показывают, что на образование гранул влияют самые различные свойства организма и среды (рис. 7.21). Общая модель кинетики образования гранулы пока еще не разработана, поскольку сложные механизмы этого явления недостаточно изучены и не вполне понятны.

При анализе роста уже образовавшихся гранул описанная модель может рассматриваться только в качестве очень грубого приближенного описания. На кинетику роста гранул должны оказывать влияние их размер, морфология и внутренняя структура, а эти факторы в свою очередь определяются совокупностью таких параметров, как интенсивность перемешивания, концентрация гранул, свойства организма и состав среды [12].

Структурированные модели кинетики клеточного роста

Неструктурированные модели описывают только количество биологической фазы. Такие модели не учитывают и никоим образом не отражают состав биофазы, т. е. то, что можно назвать ее качественными характеристиками. Если в процессе роста существенно изменяется состав клеточной популяции и если это изменение влияет на кинетику клеточного роста, то анализ таких систем возможен только с помощью структурированных моделей. Поскольку ни в одной модели практически невозможно учесть материальные балансы всех компонентов клетки, то при создании структурированной модели (по необходимости приближенной) мы, очевидно, должны тщательно отобрать ключевые переменные и процессы, играющие важнейшую роль в планируемом применении этой модели. Как мы покажем на ряде примеров в следующих разделах, структурированные модели могут быть построены на основе различных концепций.

В структурированных моделях в качестве переменных биофазы обычно применяются массовая (x_j) или молярная (с_j) концентрации в единице объема биофазы [15]. При условии полного перемешивания уравнение материального баланса по компоненту j можно записать в следующем виде:

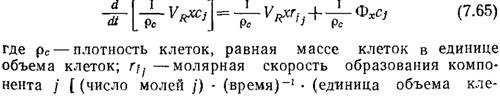
ток)^-1; Ф_х – масса клеток, вводимых в реактор в единицу времени; V_R – объем культуры; х - концентрация клеточной массы [(масса клеток) (единица объема культуры)^-1] c_j – (число молей j) (единица объема клеток)^-1].

Если это условие не выполняется (например, во втором или одном из последующих реакторов в каскаде ПРПП), то уравнение баланса должно быть соответствующим образом модифицировано.

Если допустить, что плотность клеток р_с и объем культуры V_R не изменяются во времени, то после дифференцирования уравнения (7.65) получим

Для реактора периодического действия Фх равно нулю, а выражение в скобках в правой части уравнения (7.66) есть не что иное, как удельная скорость роста µ; следовательно, для этого случая уравнение (7.66) преобразуется следующим образом:

Физический смысл r_f. ясен; выражение - µс_j отражает снижение концентрации, обусловленное разведением в процессе роста популяции клеток. Интересно, что оценка правой части уравнения (7.66) для ПРПП при стерильности питательных веществ опять-таки приводит к уравнению (7.67).