Сводные индексы в среднеарифметической и среднегармонической формах

Средний арифметический индекс физического объема, тождественный агрегатному индексу Ласпейреса, можно выразить:

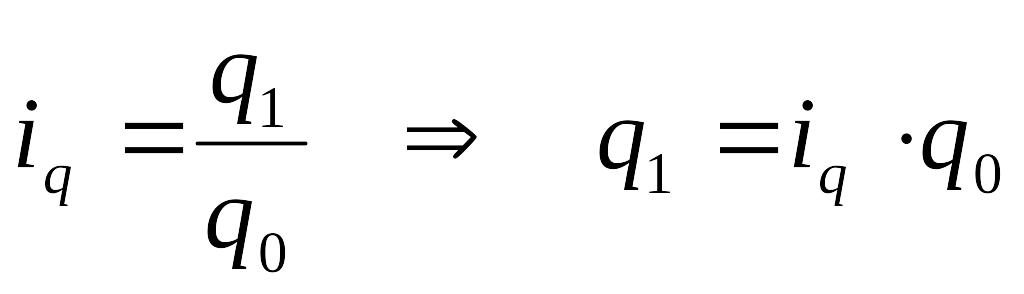
Тогда 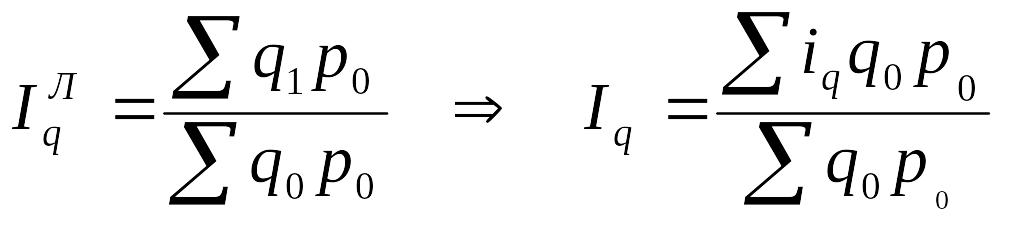(9.13)

Средний гармонический индекс цен, тождественный агрегатному индексу Пааше, можно выразить:

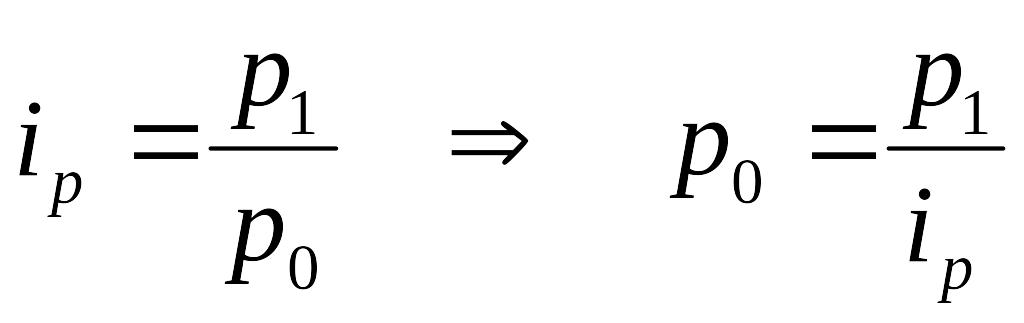
Тогда 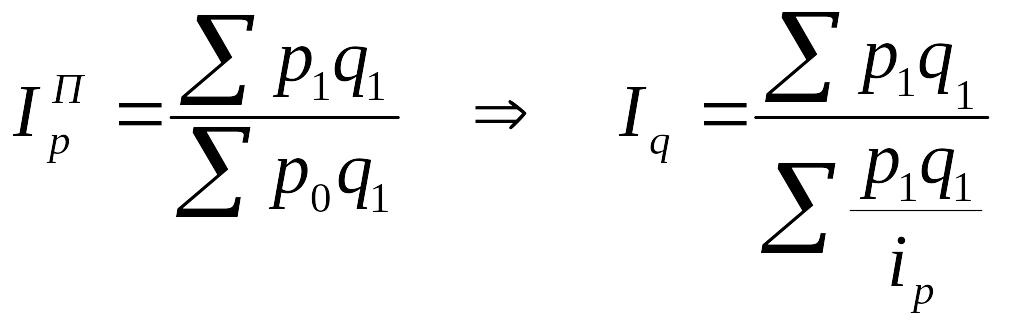(9.14)

Средний арифметический индекс цен, тождественный агрегатному индексу Ласпейреса, можно выразить:

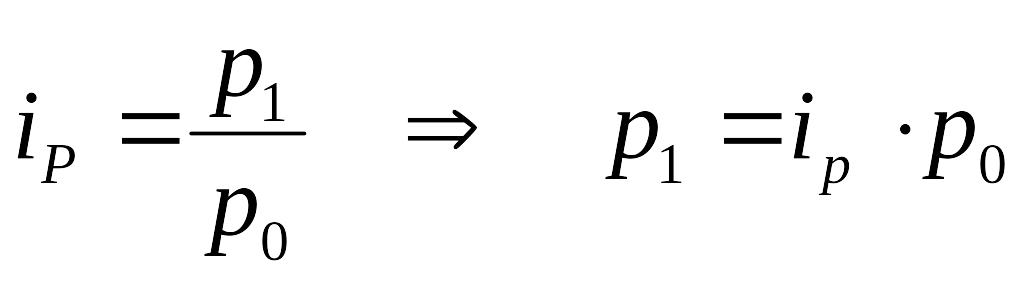
Тогда 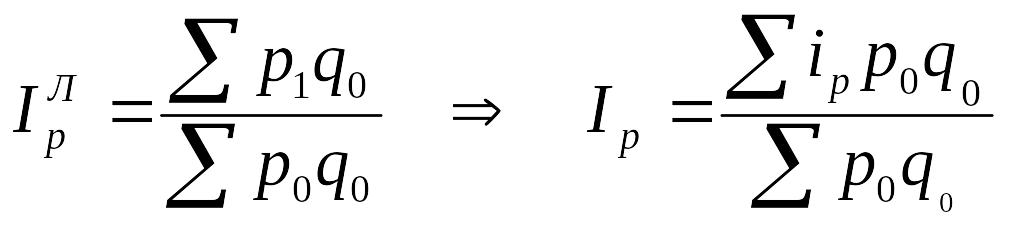(9.15)

Индексный анализ изменения взвешенной средней: индексы переменного и постоянного состава и структурных сдвигов

Индекс переменного состава представляет собой соотношение средних величин какого-либо признака в отчетном и базисном периодах:

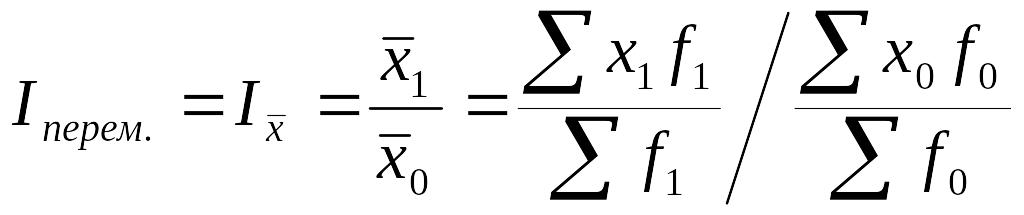(9.16)

Индекс постоянного (фиксированного) состава устраняет влияние структурного фактора:

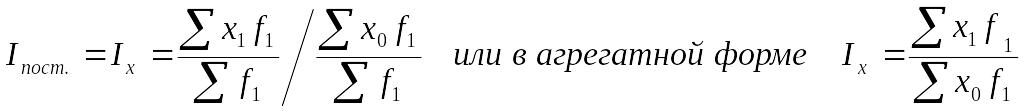(9.17)

Индекс структурных сдвигов характеризует влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака:

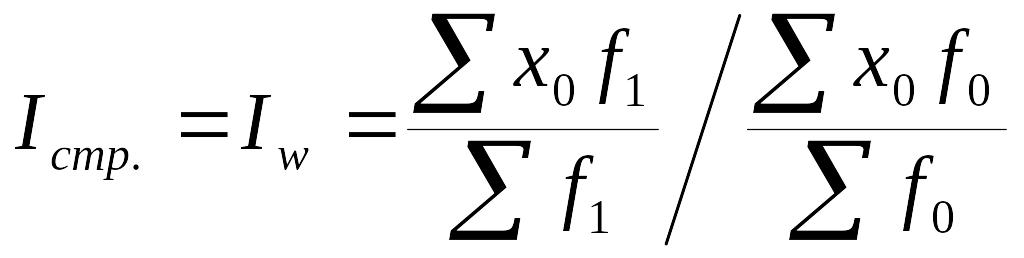(9.18)

Индексы переменного, постоянного состава и структурных сдвигов увязываются в следующую систему:

(9.19)

Ряды индексов с постоянной и переменной базой сравнения (цепные и базисные)

Цепными индексами называются индексы, которые имеют переменную базу сравнения.

Базисные индексы это индексы, имеющие постоянную базу сравнения.

Схема построения цепных индексов

И сходные уровни: q₁ q₂ q₃ q₄

Цепные индексы: 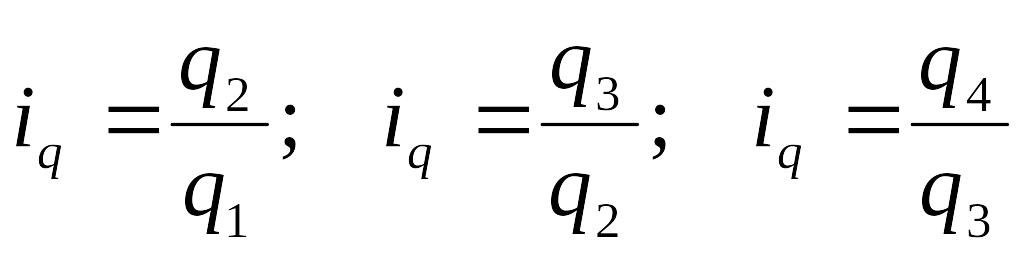(9.20)

Схема построения базисных индексов

И сходные уровни: q₁ q₂ q₃ q₄

Базисные индексы: 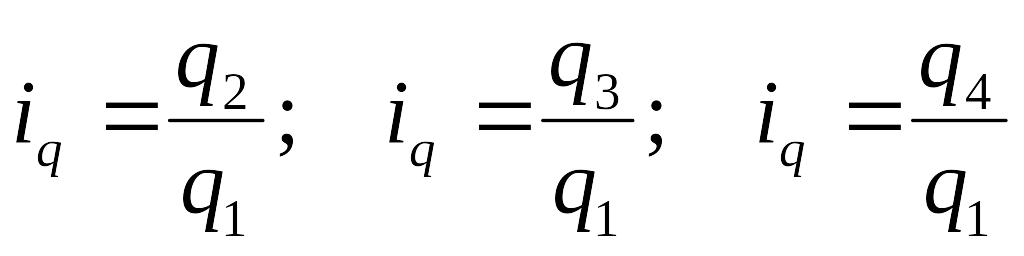(9.21)

Между цепными и базисными индексами имеется взаимосвязь, которая заключается в следующем: произведение всех цепных индексов равно общему базисному индексу:

. . = (9.22)

Отсюда следует: отношение каждого последующего базисного индекса к предыдущему базисному дает промежуточный цепной индекс:

: = ; : = (9.23)

Взаимосвязь в сводных (общих) индексах только при условии постоянства весов (или соизмерителей).

Возьмем ряд цепных индексов с постоянными весами (р₁):

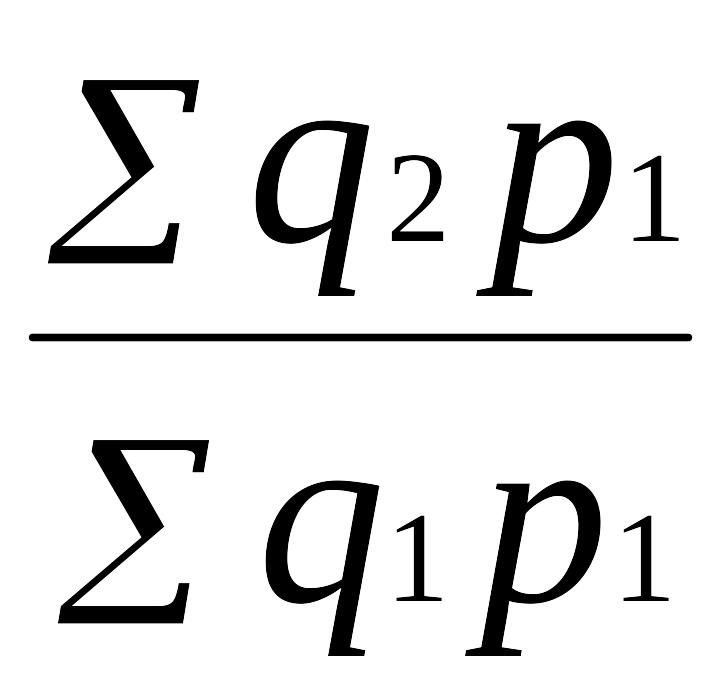I_q = 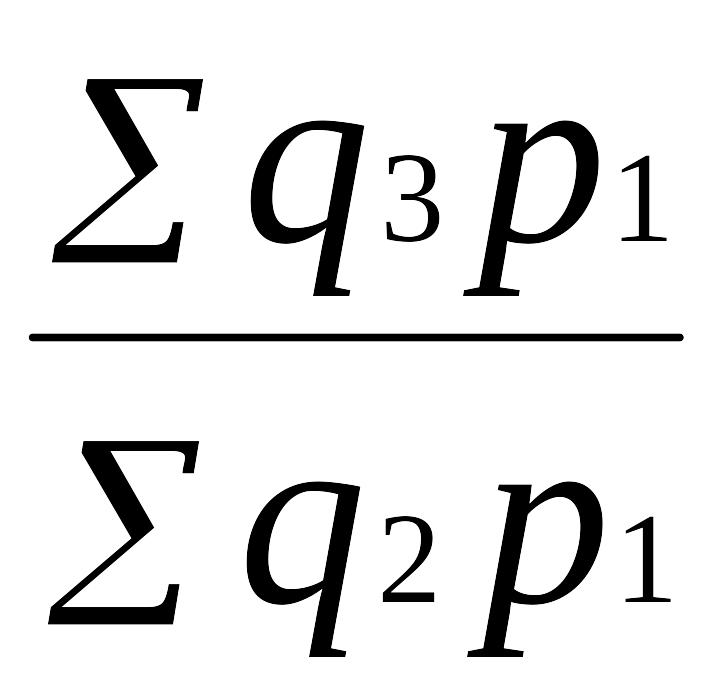; I_q = ; I_q = 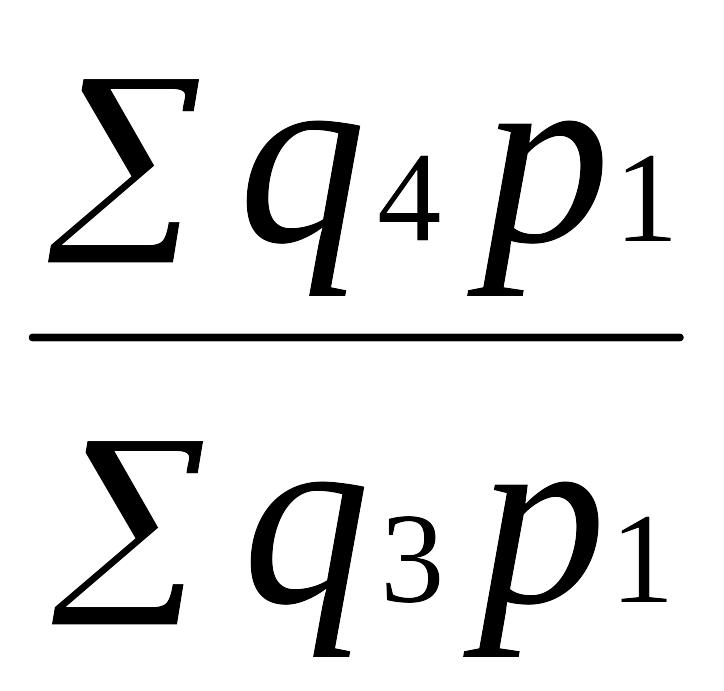(9.24)

Если перемножить эти индексы, то получим общий базисный индекс:

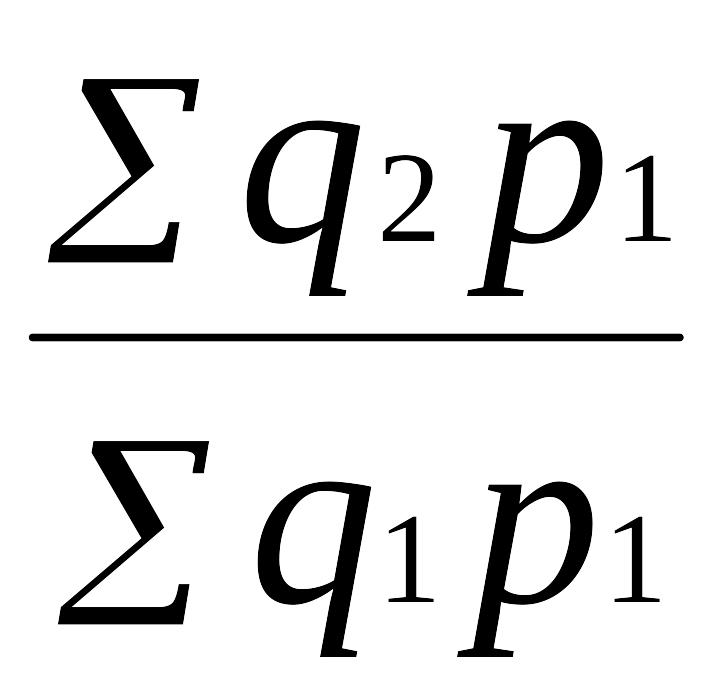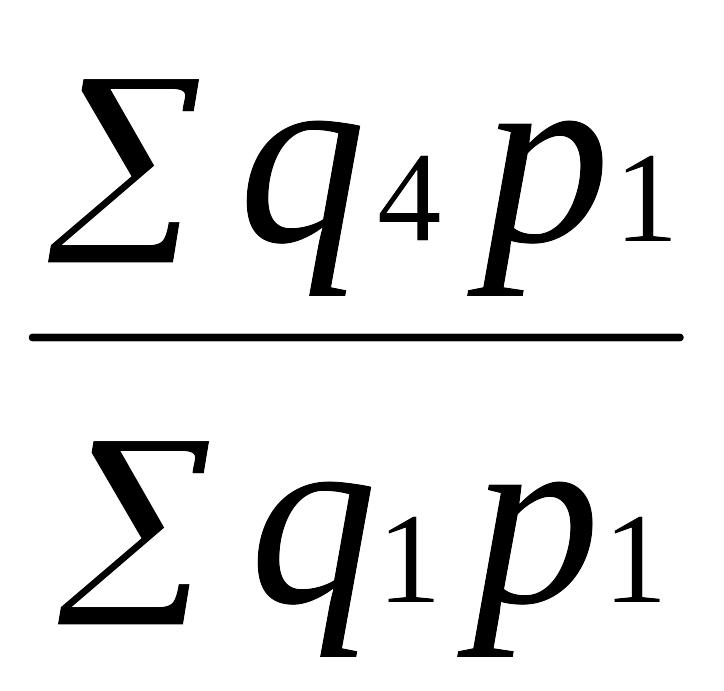. . = (9.25)

Этому требованию не отвечают индексы с переменными весами:

I_q = 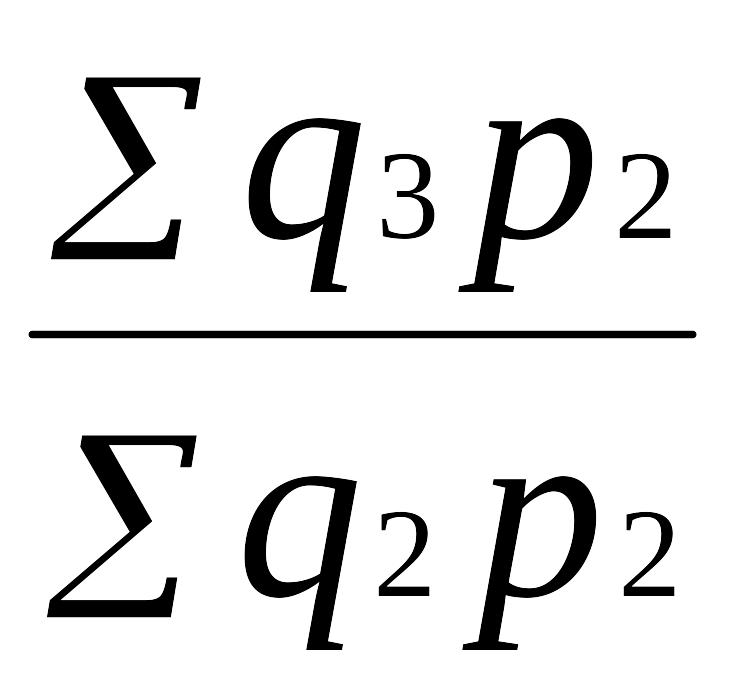; I_q = ; I_q = 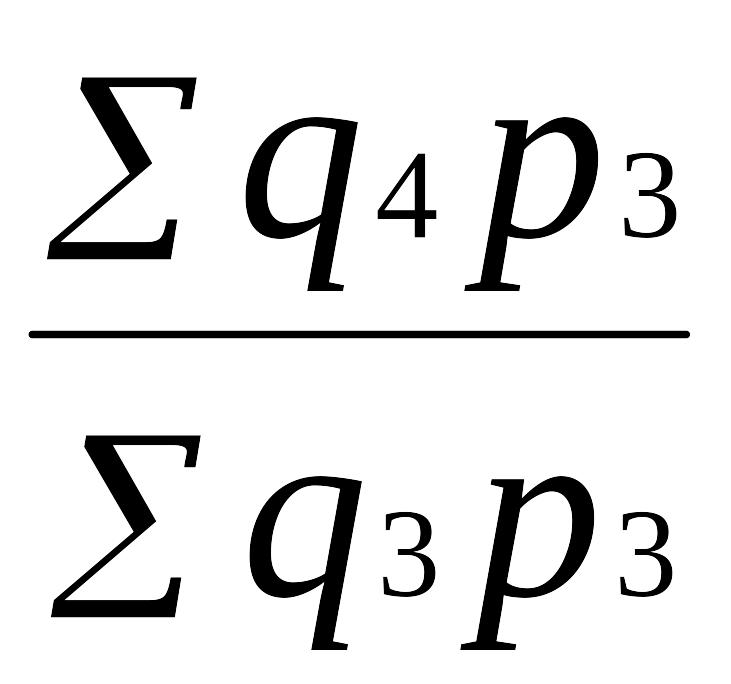(9.26)

Ряды индексов с постоянными и переменными весами

Два и более индексов с одинаковыми по содержанию и во времени весами образуют ряд индексов с постоянными весами или соизмерителями:

I_q = ; I_q = ; I_q = (9.27)

Два и более индексов с одинаковыми по содержанию, но различными во времени весами или соизмерителями называются рядом индексов с переменными весами или соизмерителями:

I_q = ; I_q = ; I_q = (9.28)

Многие связанные между собой экономические показатели образуют индексные системы. Выше были рассмотрены примеры построения двухфакторных систем взаимосвязанных индексов. Общие индексы могут быть разложены также на три, четыре и более факторных индекса, объясняющих изменение результативного признака за счет влияния каждого фактора в отдельности. Обозначим факторные признаки a, b, c, тогда система взаимосвязанных индексов будет иметь вид:

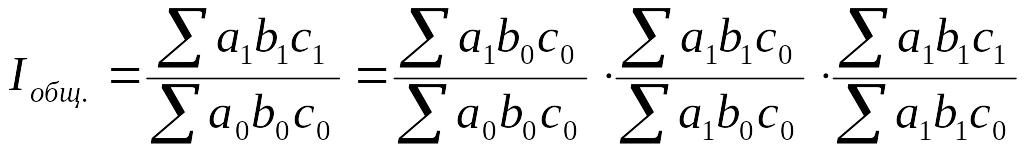(9.29)

Аналогично строится система взаимосвязанных индексов при большем количестве факторов.