Вариация альтернативного (качественного) признака. Правило сложения дисперсий для доли признака.
При статистическом выражении колеблемости альтернативных признаков наличие изучаемого признака обозначается 1, а его отсутствие – 0. Доля вариантов, обладающих изучаемым признаком обозначается р, а доля вариантов, не обладающих признаком q. Следовательно, р+q=1.
Найдем их среднее значение и дисперсию:
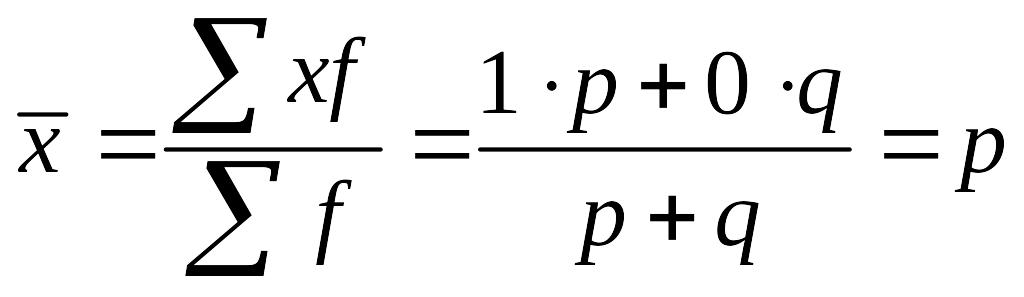(6.19)
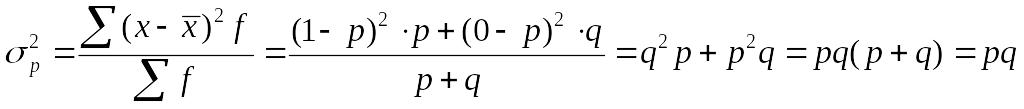(6.20)
Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, и доли единиц, не обладающих им.
Пример 6.3. На 10000 населения приходится 4000 мужчин и 6000 женщин. Определить среднее квадратическое отклонение по полу.
Решение:
Доля мужчин в населении p=4000/10000=0,4;
доля женщин q=6000/10000=0,6.
Тогда дисперсия
,
а среднее квадратическое отклонение
.
Пример 6.4. Налоговой инспекцией одного из районов города проведено 86 проверок коммерческих фирм и в 37 обнаружены финансовые нарушения. Определить среднее квадратическое отклонение числа нарушений.
Решение:
По условию n=86,
m=37,
тогда доля фирм, в которых обнаружены
нарушения, составит p=37/86=0,43;
q=1-0,43=0,57.
Дисперсия -
,
а среднее квадратическое отклонение
.
Правило сложения дисперсий распространяется и на дисперсии доли признака, то есть доли единиц с определенным признаком в совокупности, разбитой на части (группы).
Внутригрупповая дисперсия доли определяется по формуле:
(6.21)
Средняя из внутригрупповых дисперсий рассчитывается так:
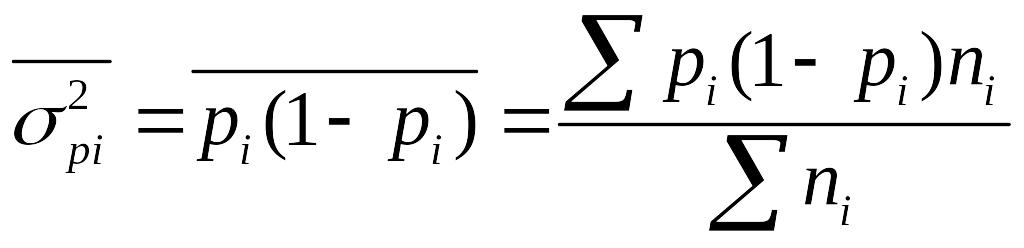(6.22)
где ni – численность единиц в отдельных группах;
Формула межгрупповой дисперсии имеет следующий вид:
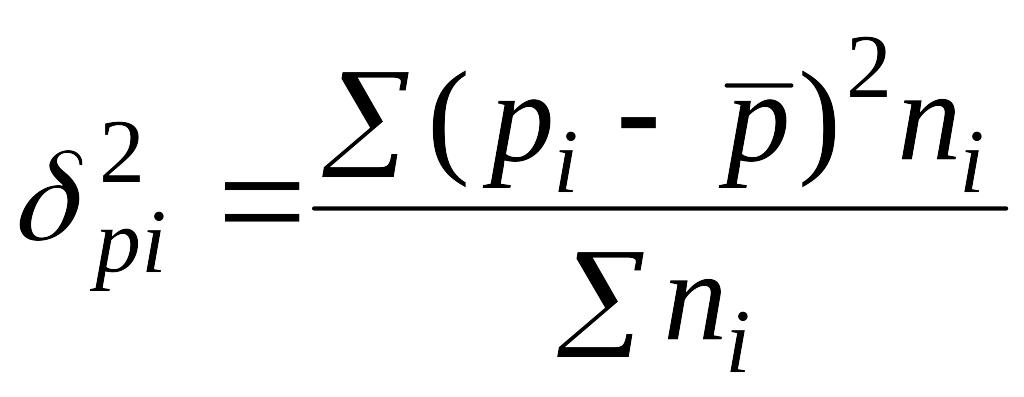(6.23)
–
доля
изучаемого признака во всей совокупности,
которая определяется по формуле:
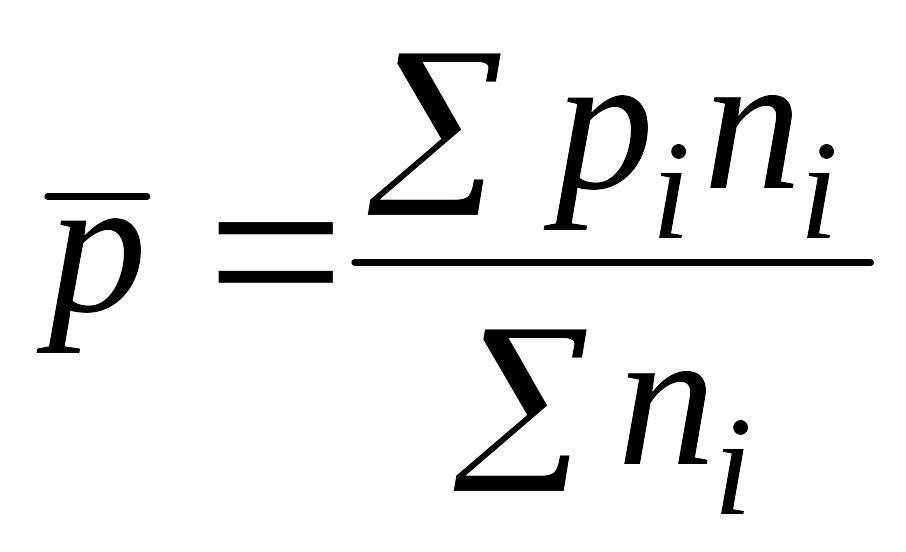(6.24)
Общая дисперсия определяется по формуле:
(6.25)
Три вида дисперсий объединены между собой следующим образом:
(6.26)
Это – правило сложения дисперсии доли признака.
Пример 6.5. Имеются следующие данные об удельном весе основных рабочих в трех цехах фирмы:
Цех |
Удельный вес основных рабочих в % (pi) |
Численность всех рабочих в % |
1 2 3 |
80 75 90 |
100 200 150 |
Итого |
- |
450 |
Определить общую дисперсию доли основных рабочих по всей фирме, используя правило сложения дисперсий.
Решение: 1)Определим долю рабочих в целом по фирме (формула 6.24.).
.
2) Общая дисперсия доли основных рабочих по фирме в целом будет равна (формула 6.25):
.
3) Внутрицеховые дисперсии рассчитаем, применив формулу 6.21.
4)Средняя из внутригрупповых дисперсий будет равна (формула 6.22.)
.
5) Межгрупповую дисперсию определим по формуле 6.23.
.
Проверка вычислений показывает: 0,154 = 0,15 + 0,004.