Меры вариации для сгруппированных данных. Правило сложения дисперсий.

При изучении вариации для сгруппированных данных выделяют три вида дисперсий: общую дисперсию, внутригрупповую (частную) дисперсию, межгрупповую дисперсию.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов.

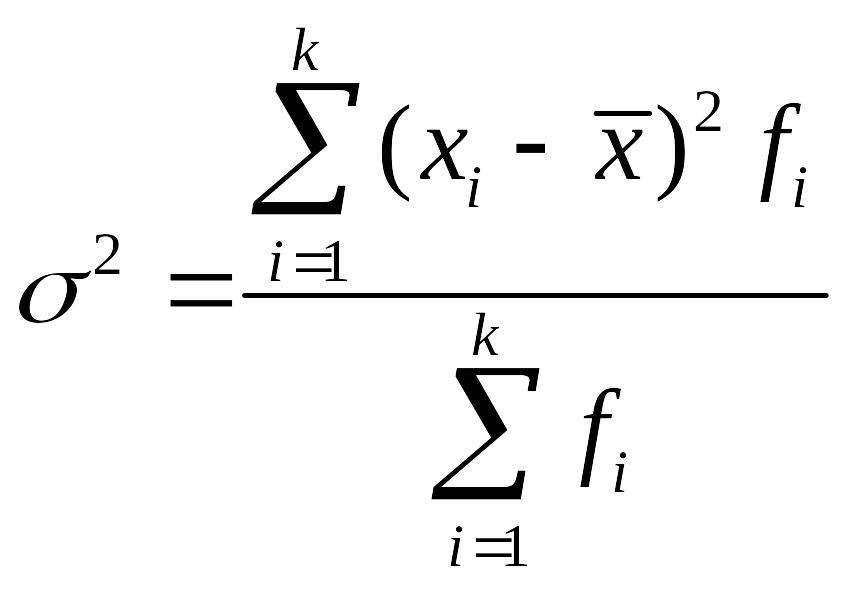(6.12)

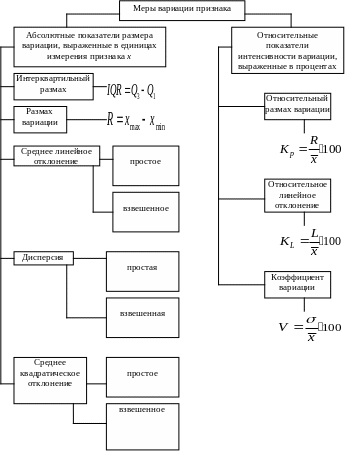
Схема 6.1.

Статистическое изучение вариации

Внутригрупповая (частная) дисперсия измеряет вариацию признака внутри группы.

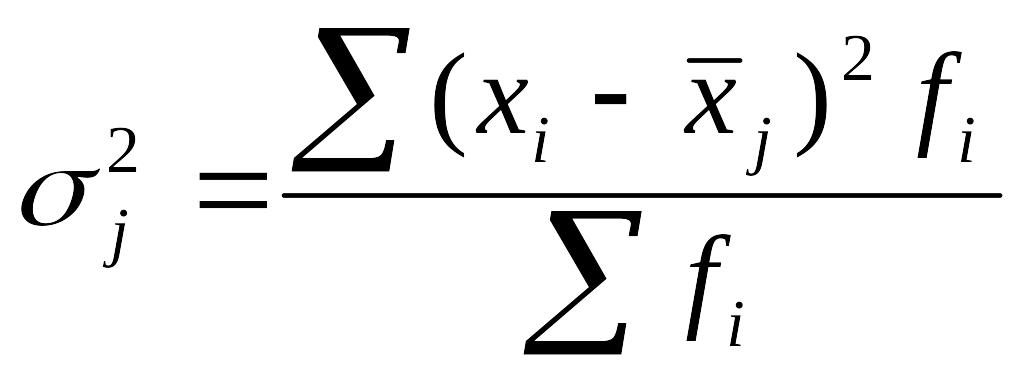(6.13)

где x_i – значения признаков внутри j-й группы; – средняя арифметическая j-й группы; f_i – частоты вариантов в j-й группе; – объем j-й группы. Суммирование и в числителе, и в знаменателе осуществляется только по тем признакам, которые попали в j-ю группу.

Средняя из внутригрупповых (частных) дисперсий.

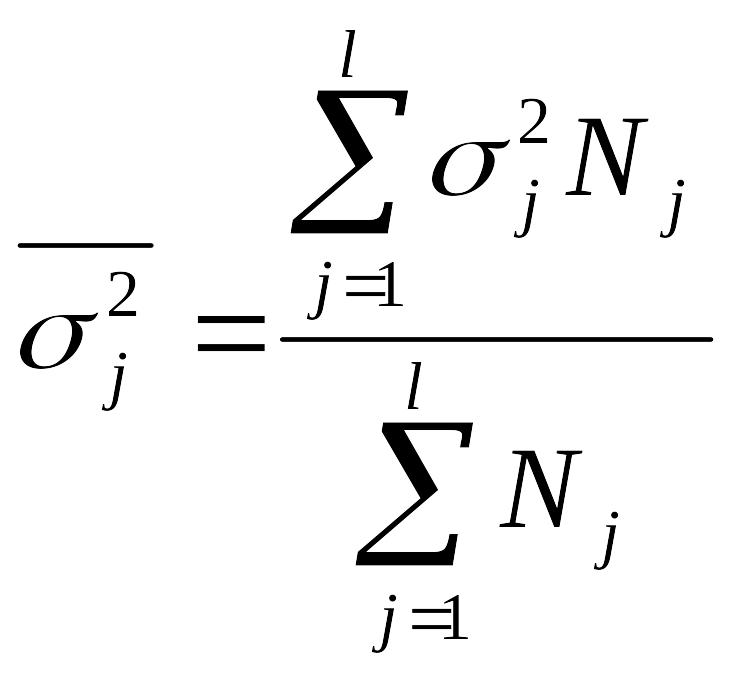(6.14)

где N_j – объем j-й группы, j=1,2,…,l (l – число групп), 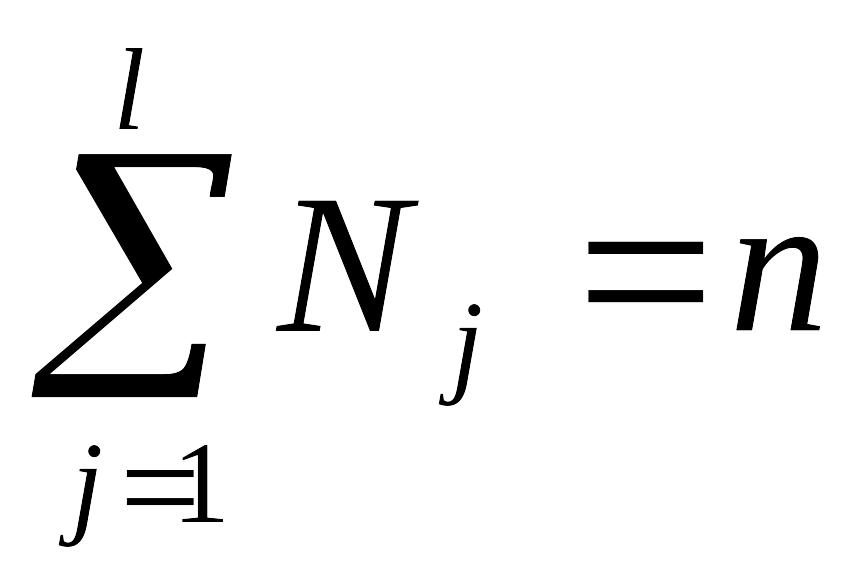- общее число признаков ряда.

Межгрупповая дисперсия измеряет колеблемость групповых средних вокруг общей средней и отражает вариацию, обусловленную признаком, положенным в основу группировки.

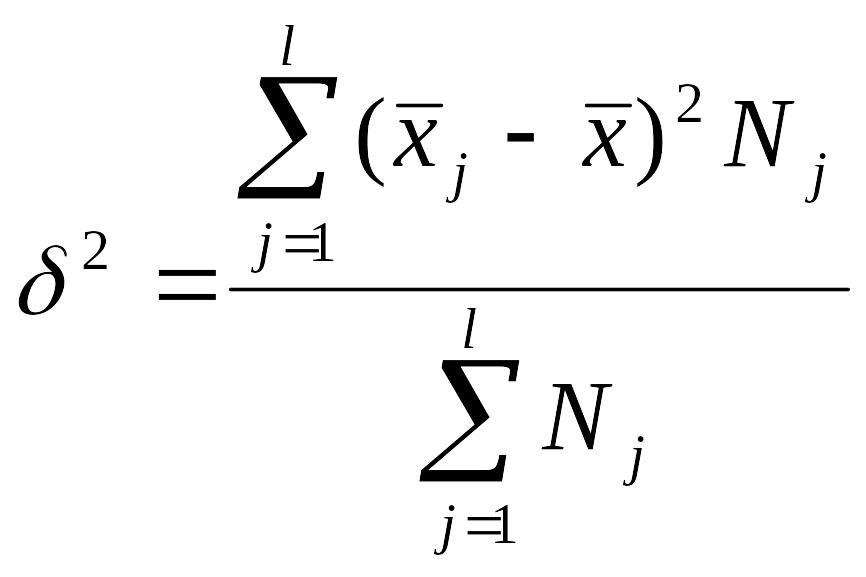(6.15)

где - общая средняя вариационного ряда.

Существует закон, связывающий три вида дисперсии.

Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий.

(6.16)

Зная любые два вида дисперсий, всегда можно найти или проверить правильность расчета третьего вида.

(6.16а)

(6.16б)

Правило сложения дисперсий позволяет оценить степень влияния группировочного признака на результативный признак и количественно измерить степень этого влияния.

Для этого применяется коэффициент детерминации, который показывает степень колеблемости в процентах результативного признака в зависимости от степени колеблемости факторного и рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака.

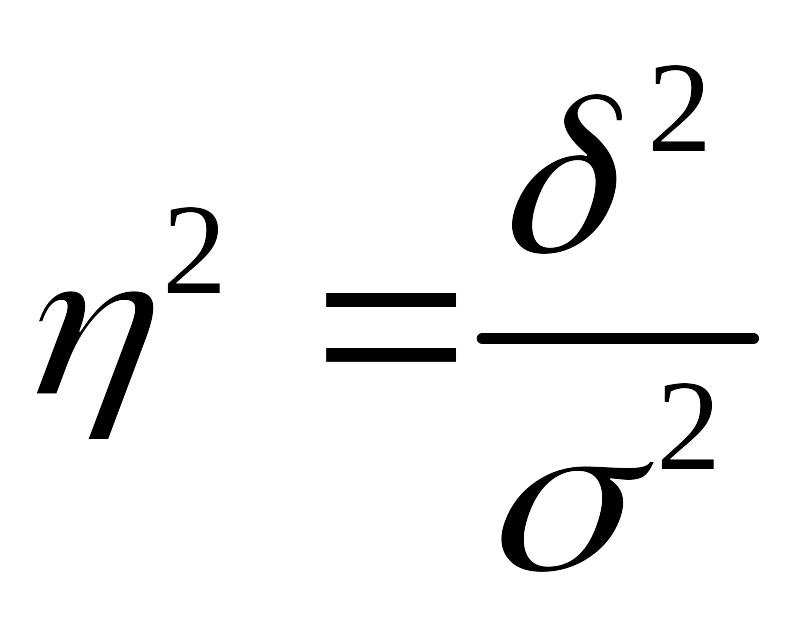(6.17)

Корень квадратный из коэффициента детерминации называют эмпирическим корреляционным отношением (ЭКО), которое показывает степень тесноты связи.

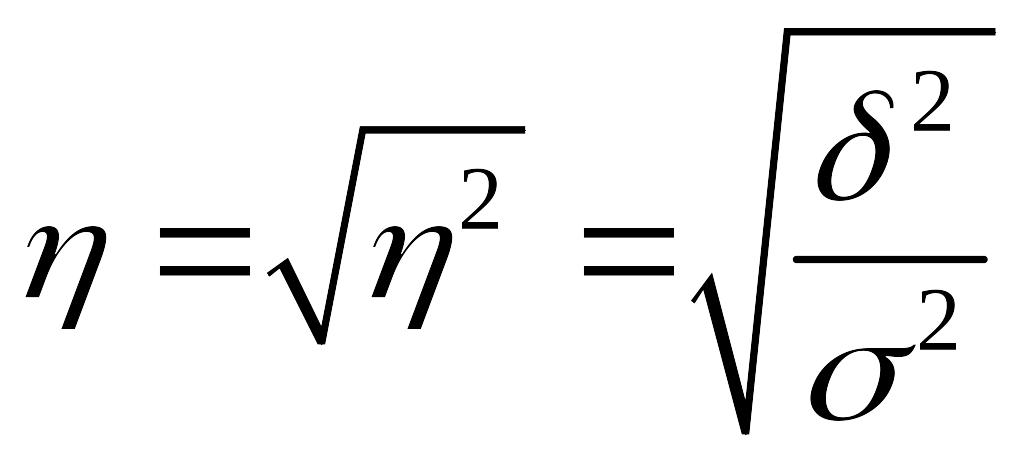(6.18)

Это показатель принимает значения в интервале [0,1]. Если связь отсутствует, то =0. В этом случае дисперсия групповых средних равна нулю ( ), то есть все групповые средние равны между собой и межгрупповой вариации нет. Если связь функциональная, то =1. В этом случае дисперсия групповых средних равна общей дисперсии ( ). Промежуточные значения  оцениваются по степени их близости к предельным.

Пример 6.2. Опрос 8 биржевых брокеров дал следующие результаты:

Брокер	Проходил ли переобучение в последние три года	Число контрактов, заключенных в день опроса
1	Да	9
2	Нет	8
3	Нет	6
4	Да	7
5	Нет	7
6	Да	8
7	Да	8
8	Нет	7

Среднее число контрактов, заключенных брокерами:

.

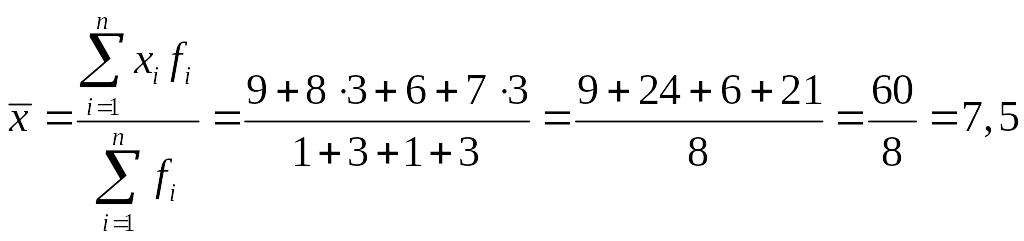В данном примере переподготовка – факторный признак, а число заключаемых контрактов – результативный.

Сгруппируем эти данные по признаку переобучения и рассчитаем средние по каждой группе.

Группы брокеров	Число брокеров	Число контрактов	Групповые средние
Прошли переобучение	4	9, 8, 8, 7	8
Не прошли переобучение	4	8, 7, 7, 6	7

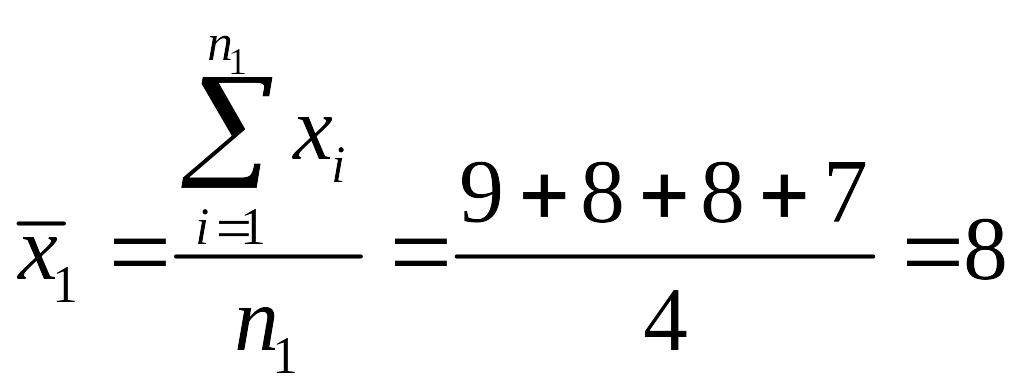, где n₁ – число признаков в первой группе.

Или по формуле для взвешенных вариант

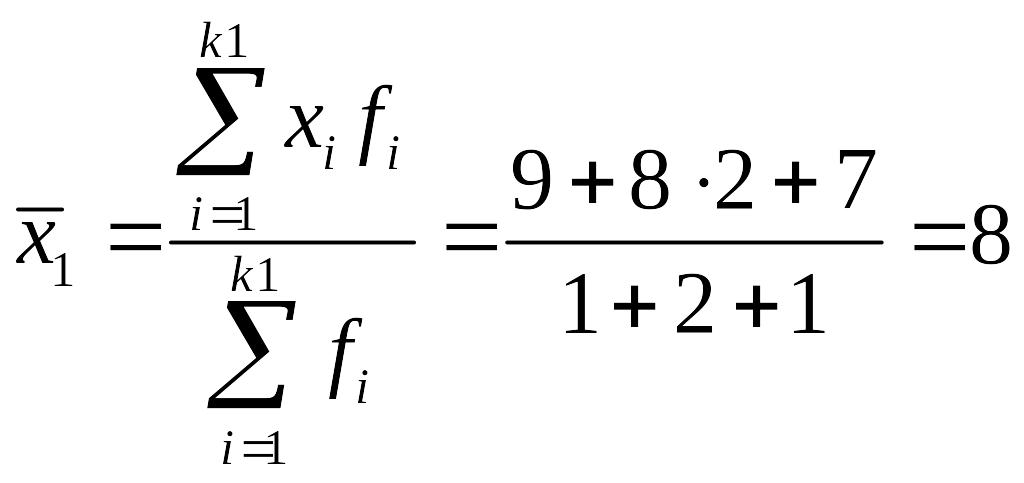, где f_i – частоты ряда.

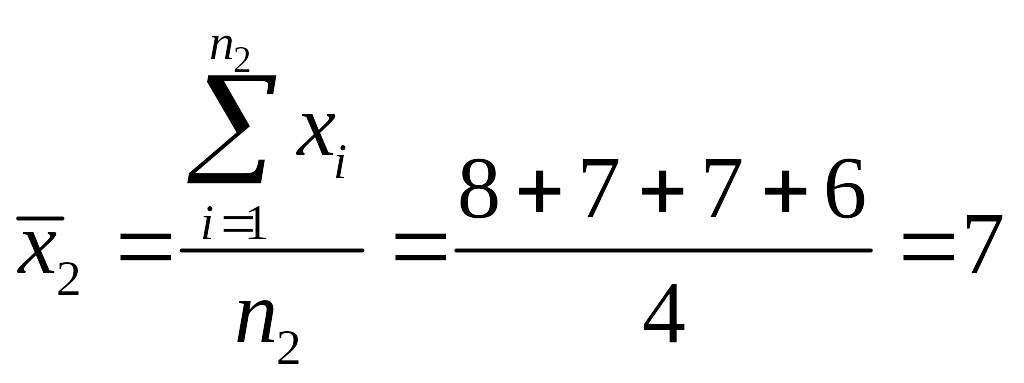, где n₂ – число признаков во второй группе.

Или по формуле для взвешенных вариант

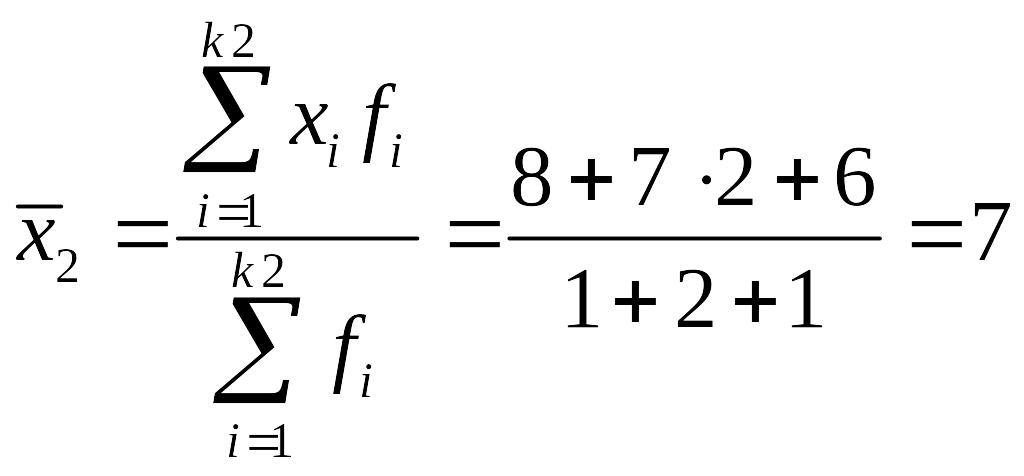, где f_i – частоты ряда.

Рассчитаем дисперсии в каждой группе.

Дисперсия числа заключенных контрактов у брокеров, прошедших переобучение:

Число контрактов Х	Частота f
9 8 7	1 2 1	1 0 -1	1 0 1	1 0 1
Итого	4	-	-	2

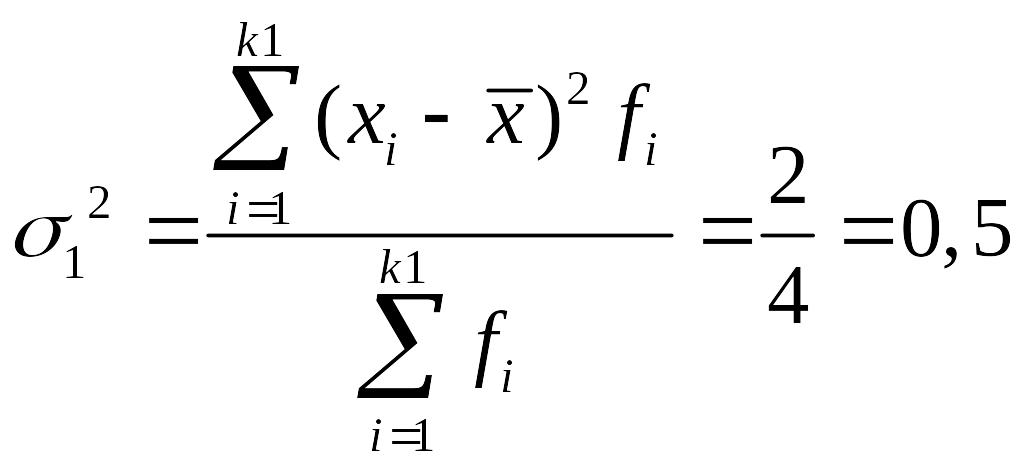
Дисперсия числа заключенных контрактов у брокеров, не прошедших переобучение:

Число контрактов Х	Частота f
8 7 6	1 2 1	1 0 -1	1 0 1	1 0 1
Итого	4	-	-	2

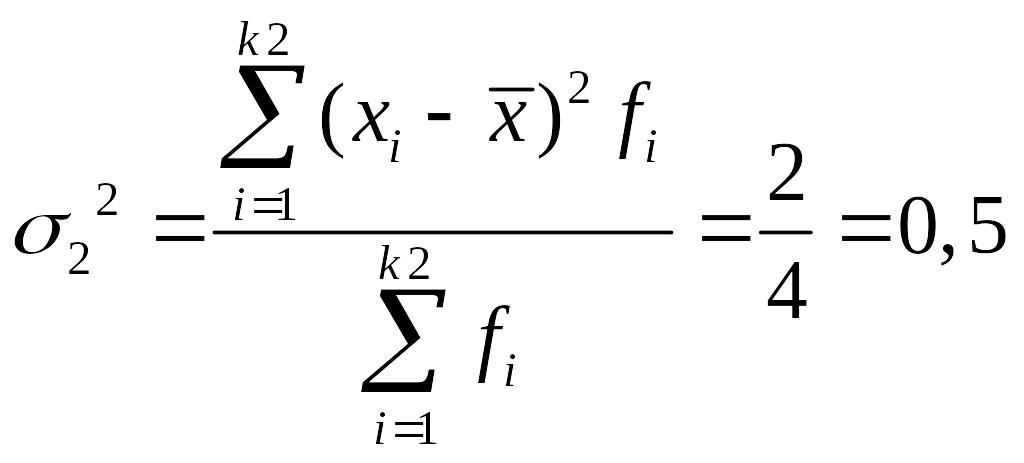
Рассчитаем среднюю из внутригрупповых дисперсий:

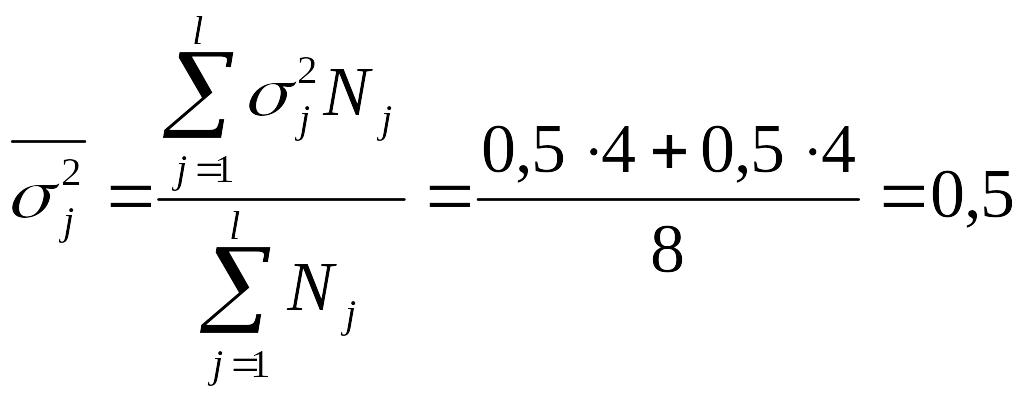
Этот показатель характеризует влияние на результативный признак всех прочих факторных признаков за исключением признака, положенного в основу группировки. Очевидно, что различие в числе заключенных контрактов в двух группах вызвано тем, что брокеры первой группы прошли переобучение, а брокеры второй группы не прошли.

Найдем дисперсию между группами (межгрупповую дисперсию).

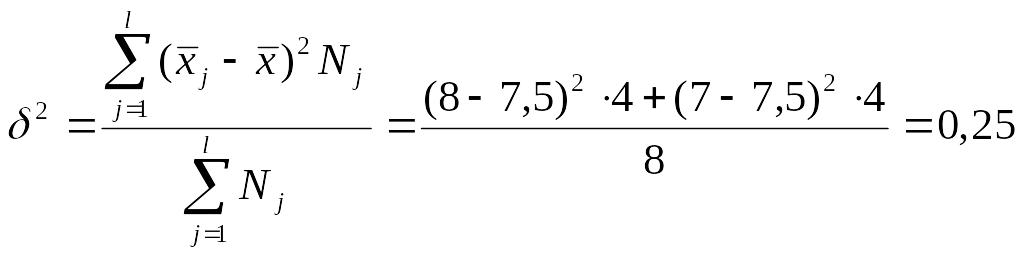
Этот показатель характеризует влияние на результативный признак факторного признака, положенного в основу группировки.

Рассчитаем общую дисперсию числа заключенных контрактов.

Число контрактов Х	Частота f
9 8 7 6	1 3 3 1	1,5 0,5 -0,5 -1,5	2,25 0,25 0,25 2,25	2,25 0,75 0,75 2,25
Итого	8	-	-	6,0

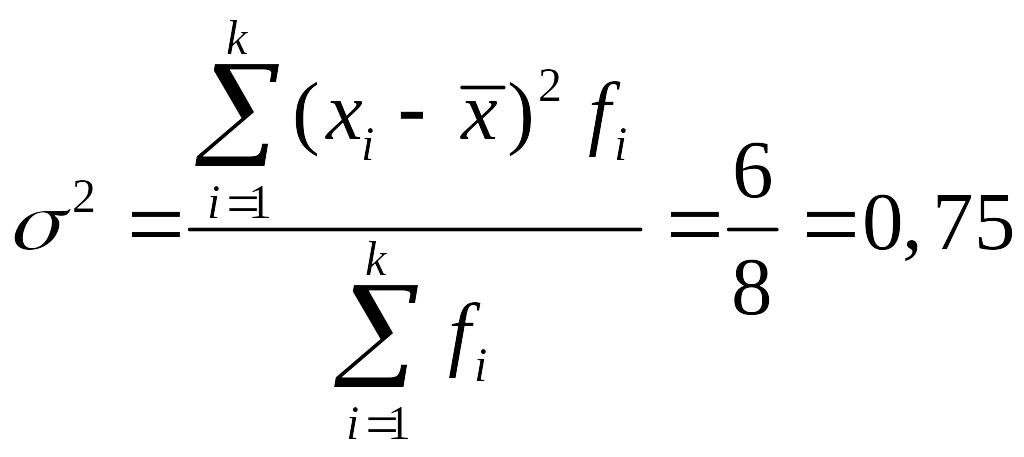
Итак, по данным примера имеем , , . Тогда по правилу сложения дисперсий получаем 0,75 = 0,5 + 0,25.

Рассчитаем коэффициент детерминации: или 33%. То есть вариация числа заключенных контрактов на 33% объясняется фактором переобучения, 67% - это влияние прочих факторов.

Эмпирическое корреляционное отношение: 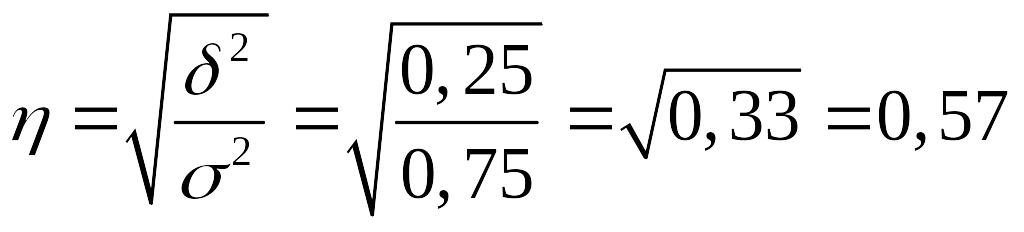. Следовательно, фактор, положенный в основу группировки, существенно влияет на число заключаемых брокерами контрактов, но существуют и другие факторы, влияние которых тоже значительно.