4.9.2. Исчисление предикатов. Общезначимость

Описанная в предыдущем параграфе система по существу представляет собой исходную точку для формулирования различных исчислений предикатов. Отличительные особенности классического исчисления предикатов (которое мы рассматриваем) включают в себя дальнейшие положения, распространяющие единственное допущение, относящееся к исчислению высказываний, а именно, что к простой формуле поставлено в соответствие только одно истинное значение 1 или 0 (истина или ложь).

Формулы в исчислении предикатов гораздо сложнее, чем формулы логики высказываний. Соответственно этому указан^ ное выше допущение мы введем несколькими последовательными шагами.

Прежде всего примем, что данной системе поставлено в соответствие непустое множество D, называемое полем {предметной областью, множеством или областью интерпретации), что каждая предметная переменная черпает свои значения в D. Примем далее, что каждому n-местному предикатному символу поставлена в соответствие логическая функция, т. е. функция, определенная на D со значениями (1,0). (Для 0-местного предиката поставленную ему в соответствие функцию примем за постоянную 1 или 0.)

Примем, наконец, что простой формуле Р(у 1, у2,. уп приписывается истинностное значение, связанное с приписыванием элементов из поля D каждой переменной из числа yl, у2,. уп, следующим образом. Если переменной yi приписывается элемент di поля!) и если предикатному символу Р(х1, х2, . хп) приписывается значение f, то истинностное значение для Р(у1, у2, . , уn) будет f (dl, d2, . dn).

Например, если Р(х, у, х) есть простая формула и формуле Р (х, у, z) приписывается значение f, то истинностное значение Р (х, у, х), связанное с приписыванием элемента а переменной х и элемента в переменной^, будет f (а,в, а). Вышеизложенное служит основой оценочной процедуры для формулы С в исчислении предикатов. В этой процедуре предполагается, что дано поле D; каждому предикатному символу, входящему в него, ставится в соответствие функция и 3) каждой из свободных переменных в С приписывается значение в D. Взятые вместе эти три положения задают приписывание для формулы С. В качестве примера рассмотрим вопрос о приписывании истинностных значений формуле

(х)(Р(х) и Q) V (Q & Р(у)).

Хотя поле фиксировано, оно неизвестно. Предположим, что D=(a, в). По предположению формуле Р(х) поставлена в соответствие логическая функция, определенная на D со значениями в {1, 0}, а формуле Q некоторое истинностное значение. Далее свободная переменная принимает любое значение в поле D.

Логические функции могут быть поставлены в соответствие формуле Р (х), даны ниже в таблице:

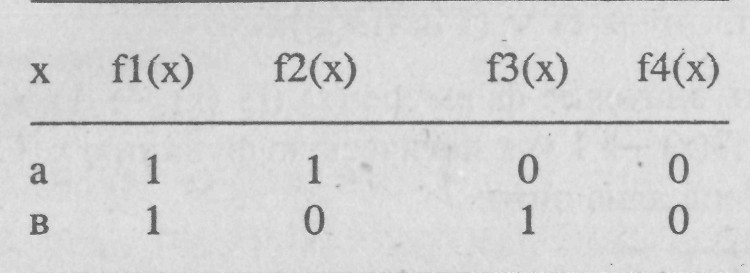
Значениями, которые можно поставить в соответствие формуле, являются 1 и 0 , а у можно приписать значение а или в. Таким образом, мы можем внести в таблицу 16 строк распределения значений, показывая возможные случаи распределения истинностных значений:

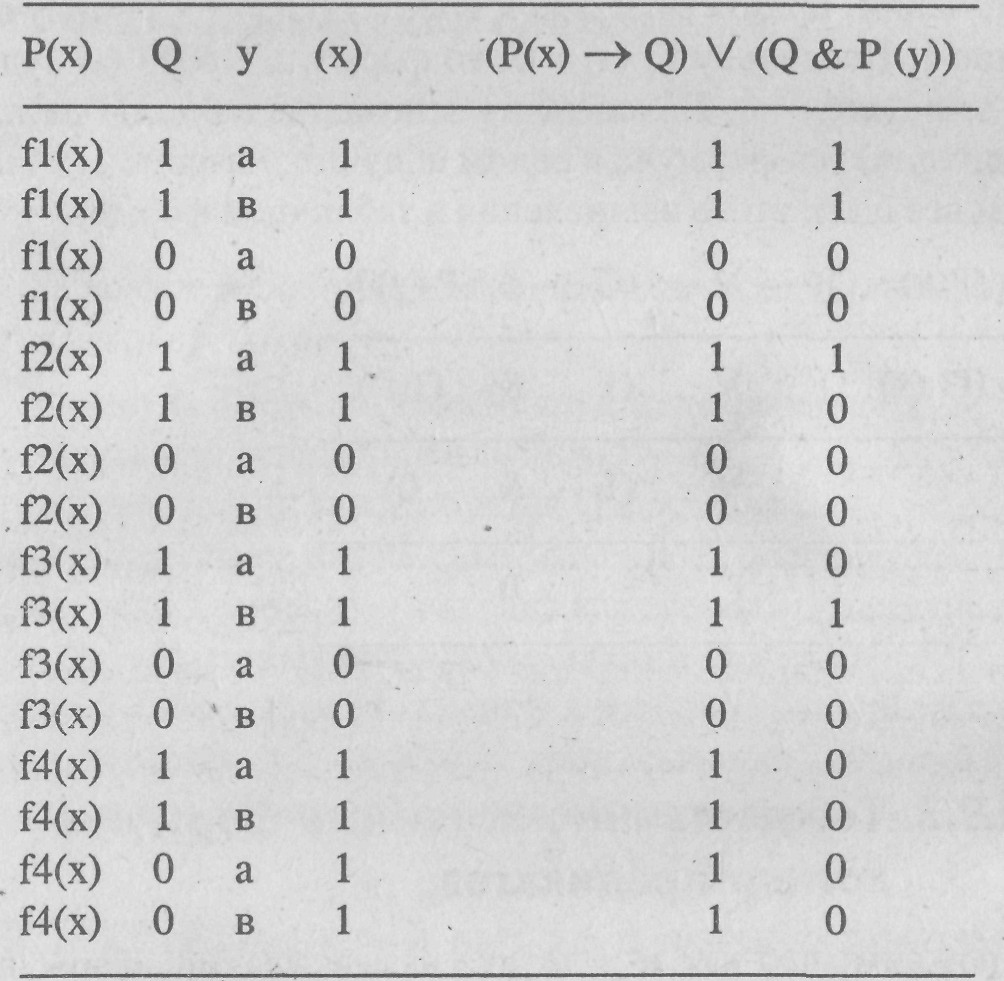
Значения, стоящие в столбцах под Р(х), Q и у в какой-либо строке, составляют приписываемые рассматриваемой формуле значения. Подробности вычисления, связанные, например, с приписывание значений, внесенных в девятую строку табли-

цы, заключаются в следующем. Сперва мы подставляем приписываемые значения в формулу и получаем

Чтобы приписать значение формуле •, мы

должны вычислить как логическую функцию х. Со-

ответствующая таблица дана ниже:

Поскольку истинностное значение импликации есть 1 для всех значений, приписываемых получит

значение 1. Поскольку f3 (а) = 0, то формула 1 & f3 (а) будет иметь значение — 0. Наконец, на основании таблицы для V (дизъюнкции) вся формула в целом получит значение 1 .Резюмируем все шаги этого вычисления в табличной форме: