4.5.1. Понятие тождественно-истинной формулы
Каждая
тождественно-истинная формула выражает
какой-то логический закон. Формула
есть
известный логический закон тождества,
а формула
—
закон исключенного третьего.
Рассмотрим еще два примера тождественно-истинных формул.
Формула
имеет
следующую таблицу:
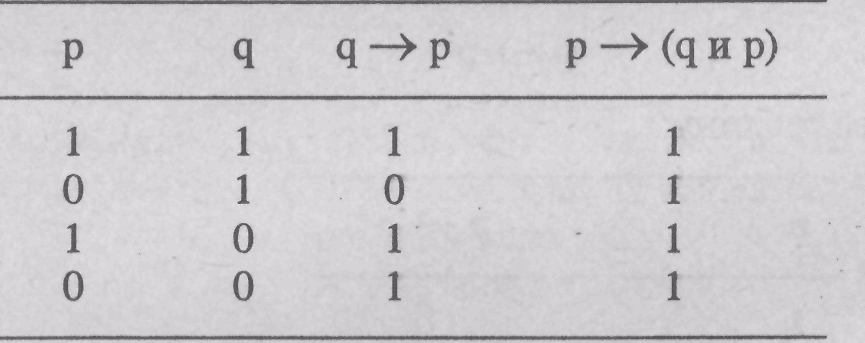
а формула
(закон
гипотетичес-
кого силлогизма) — имеет следующую таблицу:
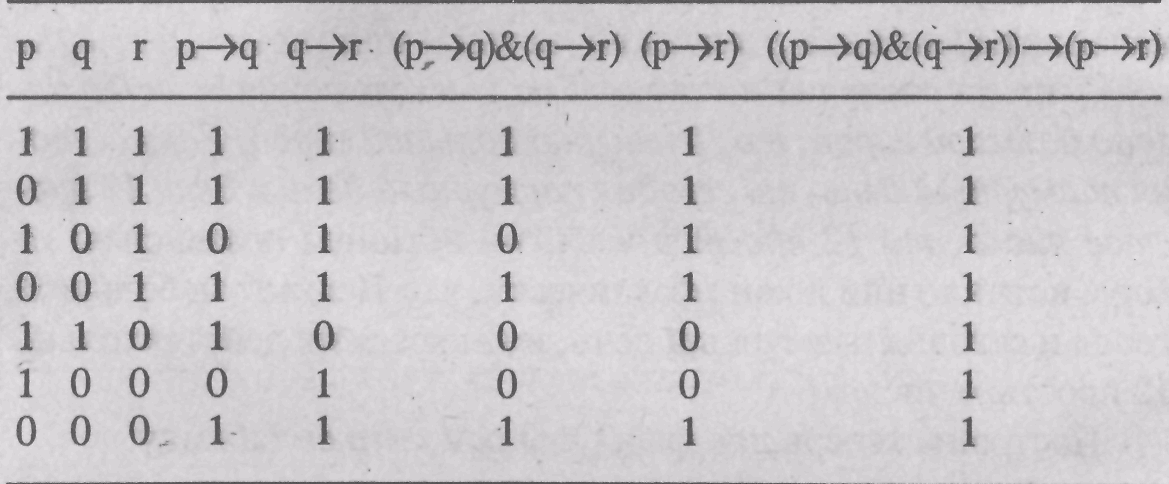
Таким образом, существуют формулы, которые истинны при любых логических значениях своих переменных. Ясно, что все тождественно-истинные формулы равносильны друг другу. Поскольку соответствующие этим формулам сложные высказывания истинны при любом конкретном содержании и
независимо от, фактической истинности элементарных высказываний, из которых они состоят, говорят, что они являются аналитически или логически истинными высказываниями. Тождественно-истинные формулы и соответствующие конкретные высказывания всегда истинны потому, что в их логической структуре (логической форме) отражаются объективные связи, которые носят общий и закономерный характер.
4.5.2. Понятие тождественно-ложной формулы
Существуют также формулы, которые при любых наборах логических значений переменных получают в заключительном столбце своей таблицы логическое значение «ложь». Они называются тождественно-ложными (противоречивыми) формулами.
Рассмотрим, например, формулу р & ~ р, которая имеет следующую таблицу:
Рассмотрим далее
формулы:
которые имеют следующие таблицы:
Ясно, что все
тождественно-ложные формулы равносильны
друг другу. Отрицание тождественно-истинной
формулы есть тождественно-ложная
формула, и наоборот. Так, если
формулы
тождественно-истинны,
то
формулы
тождественно-ложны.
4.5.3. Некоторые свойства тождественно-истинных формул:
1.
Если формулы
—
тождественно-истинны,
то формула
—
тождественно истинная формула
2. Формула
А равносильна формуле В тогда и только
тогда, когда формула
—
тождественно-истинная
формула.
4.6
НОРМАЛЬНЫЕ ФОРНЫ И ПРОБЛЕМА РАЗРЕШИМОСТИ
4.6.1. Понятие нормальной формы
Определение
:Формула логики высказываний имеет
нормальную форму, если она: а) не содержит
знаков
б) знаки отрицания
стоят в ней только при переменных.
Например, формула
имеет нормальную форму, а формула
не имеет.
4.6.2. Процедура приведения к нормальной форме
Любую формулу А, не имеющую нормальной формы, можно конечным числом применений правила замены преобразовать в формулу А', которая имеет нормальную форму. Процесс такого преобразования будем называть процессом приведения формулы к нормальной форме.
Для того чтобы данную формулу привести к нормальной форме, необходимо произвести в ней следующие равносильные замены:
1) каждую
подформулу вида
заменить
согласно равносильности (17) формулой
I;
2) каждую
подформулу вида
заменить
согласно равносильности (16) формулой
3) каждую
подформулу вида
заменить
согласно равносильности (13) формулой
;
4) каждую
подформулу вида
заменить
согласно равносильности (10) формулой
;
5) каждую
подформулу вида
заменить
согласно равносильности (11)
формулой
;
6) каждую
подформулу вида
заменить
согласно равносильности (1) формулой А.
Формула имеет нормальную форму, если ни один из перечисленных пунктов 1) — 6) настоящего предписания к ней не применим.
после чего, дважды применяя правило замены, согласно равносильности (11) — формулу
Наконец, трижды применяя правило замены, согласно равносильности (1) получаем следующую формулу в нормальной форме:
