4.3.1. Порядок логических действий

Вообще, если каждой пропозициональной переменной некоторой формулы придать определенное логическое значение, то с помощью таблиц можно определить, какое логическое значение получает в этом случае вся формула.

Пусть, например,

формула и пусть переменные р, q и г принимают соответ-

ственно логические значения «ложь», «истина» и «ложь». С помощью таблиц для логических знаков вычисляем последовательно логические значения подформул данной формулы:

«истина», «ложь»,

((р & ~ (q) и ~ —г) — «истина», и, наконец, находим, что вся формула имеет логическое значение «истина».

Вычисление логического значения формулы по заданным логическим значениям ее переменных удобно проводить следующим образом. Выпишем формулу в одну строку и под пропозициональными переменными напишем их логические значения. Затем в соответствии с шагами построения формулы под каждым логическим знаком выписываем логическое значение подформулы, в которой этот знак является главным. Логическое значение формулы будет написано под ее главным логическим знаком. Например, для рассмотренной выше формулы получаем запись:

По каждой формуле логики высказываний всегда можно построить отвечающую ей таблицу, в которой зафиксировано, какие логические значения будет получать данная формула при различных наборах логических значений своих переменных. Таблицу формулы мы будем строить следующим образом.

Составляем список пропозициональных переменных, входящих в данную формулу. Переменные в этом списке должны быть выписаны без повторений. Затем для каждой переменной строим соответствующий ей входной (начальный) столбец таблицы. В каждой строке построенных таким образом входных столбцов выписываем некоторый отличный от остальных набор логических значений для всех пропозициональных переменных. Если п — число входных столбцов, то число строк, содержащих все различные наборы логических значений п переменных, равно 2 в степени п.

Далее, в последовательности, определяемой порядком построения данной формулы из ее подформул, для каждой подформулы, которая отлична от переменной, строим соответствующий ей столбец таблицы. Последний столбец, который назы-

вают заключительным (выходным), соответствует данной формуле. Заполнение этих столбцов логическими значениями осуществляется на основе приведенных выше таблиц для логических знаков.

4.3.2. Табличный способ исчисления истинностных значений

Построим, например, таблицу для формулы

Так как список пропозициональных переменных этой формулы содержит четыре переменные р, q, r, s, то таблица имеет четыре входных столбца и 16 строк. Остальные три столбца соответствуют всем подформулам данной формулы, отличным от переменных, причем последний является заключительным столбцом. Строки в этих столбцах заполнены на основании таблицы для логических знаков V, и &.

В результате имеем следующую таблицу.

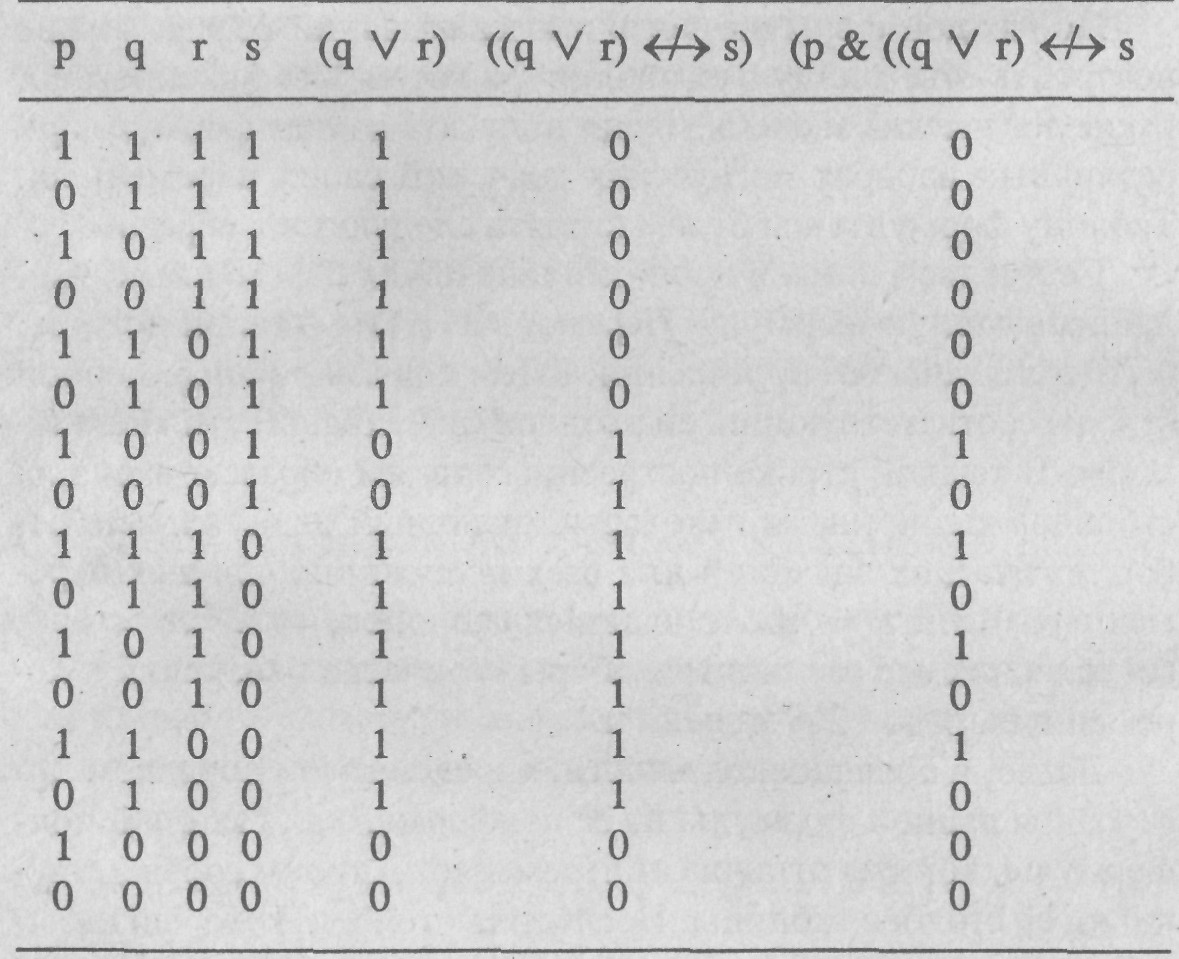
Из таблицы видно, что приведенная формула истинна для четырех наборов логических значений своих переменных и ложна для двенадцати остальных. Она отражает логическую структуру множества конкретных высказываний и, в частности, логическую структуру сложного высказывания.

Процедуру составления таблицы можно упростить, заменив ее процедурой выписывания под всеми подформулами данной формулы их логических значений.

Напишем формулу в одну строку и под первыми вхождениями каждой из пропозициональных переменных выпишем столбец ее логических значений таким образом, чтобы были представлены все возможные наборы логических значений пропозициональных переменных данной формулы. Затем под каждым из остающихся вхождений некоторой переменной выпишем тот же столбец, который выписан под ее первым вхождением. Далее, шаг за шагом под каждым логическим знаком выписываем столбец логических значений той подформулы, для которой данный логический знак является главным.

4.4

ДВОЙСТВЕННОСТЬ ЛОГИЧЕСКИХ ФОРМУЛ. РАВНОСИЛЬНЫЕ ФОРМУЛЫ

Знаки & и V, а также знаки являются двойствен-

ными логическими знаками.

Определение.

Пусть А формула, в которую не входит знак Формулой, двойственной А, называют формулу , которая получается из А заменой каждого вхождения знаков & и соответственно двойственными им знаками V и и заменой каждого вхождения знаков V и в А соответственными им знаками V и

Например, если А — формула

то двойственная ей формула А* будет иметь вид

Ясно, что если формула А* двойственна формуле А, то и, наоборот, формула А двойственна формуле А*.

Рассмотрим таблицы для конъюнкции и дизъюнкции. Можно видеть, что если в таблице для конъюнкции во всех трех столбцах для А, В и (А & В) все логические значения «истина» заменить логическими значениями «ложь», а все логические значения «ложь» — логическими значениями «истина», то получим таблицу формулы (А V В). Если же в таблице формулы (А V В) аналогичным образом во всех трех столбцах для А, В (А V В) поменять все логические значения на противоположные, то получим таблицу формулы (А & В). Эти соотношения находят выражение в равносильностях (15) и (14).

То же самое имеет место в отношении таблиц для эквивалентности и строгой дизъюнкции; таблица формулы переходит при взаимной замене логических значений во всех трех столбцах в таблицу формулы а таблица фор-

мулы — в таблицу формулы Эти соотно-

шения находят выражение в равносильностях (32) и (31).

Можно видеть также, что таблица для отрицания при подобной замене переходит в саму себя.