4.2.5. Семантическая таблица эквивалентности

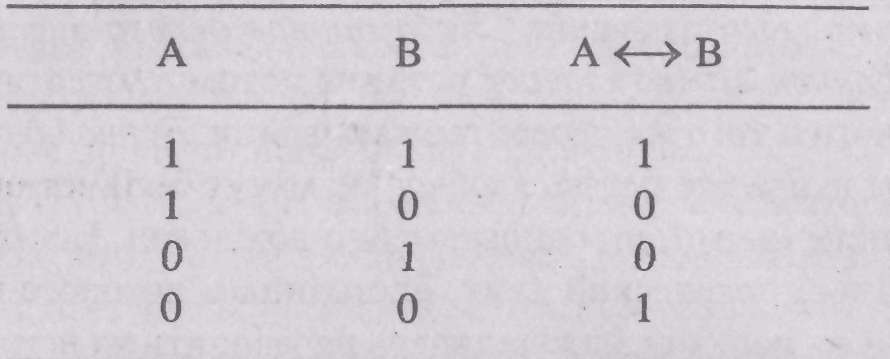
Формула истинна либо когда формулы А и В обе

истинны, либо когда они обе ложны. Например, сложное высказывание Данный прямоугольник — квадрат тогда и только тогда, когда все стороны данного прямоугольника равны истинно потому, что когда истинно высказывание Данный прямоугольник — квадрат истинно и высказывание Все стороны данного прямоугольника равны, а когда ложно высказывание Данный прямоугольник — квадрат, то ложно и высказывание Все стороны данного прямоугольника равны. И сложное высказывание было бы ложным, если нашелся бы прямоугольник, относительно которого истинно высказывание Данной прямоугольник — квадрат, но ложно высказывание Все стороны данного прямоугольника равны или если бы нашелся прямоугольник, относительно которого ложно высказывание Данный прямоугольник — квадрат, но истинно высказывание Все стороны данного прямоугольника равны.

4.2.6. Семантическая таблица

исключающей (строгой) дизъюнкции

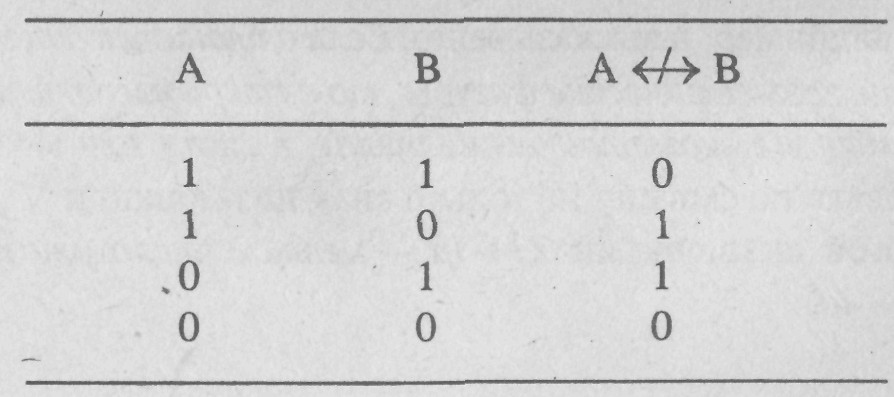
Формула истинна, когда А ложно, но В истинно,

или когда А истинно, но В — ложно. В остальных случаях она — ложна.

Например, высказывание Либо данное дерево лиственное, либо данное дерево хвойное истинно потому, что относительно одного и того же дерева высказывания Данное дерево лиственное и Данное дерево хвойное не могут быть ни одновременно истинными, ни одновременно ложными. Построив искусственный логический язык, постоянным которого придан точный смысл, мы можем теперь переводить на него выражения естественного языка. Перевод с обычного разговорного языка на язык логики высказываний осуществляется в результате содержательного анализа смысла предложений. Отсутствие формальной процедуры перехода от высказываний к формулам объясняется тем, что в естественных языках нет однозначного соответствия между смыслом и способами его выражения. В них обычно имеется несколько различных способов выражения одной и той же мысли (явление синонимии), а одно и то же предложение может выражать разные мысли (явление омонимии).

Перевод с естественного языка на язык логики высказываний затрудняется, в частности, синонимией и омонимией, которые связаны со словами естественного языка, выражающими логические постоянные. Например, знаку —>, точный смысл которого в языке логики высказываний определяется таблицей, соответствуют в естественном языке не только слова если., то, но иногда также слова когда., тогда (когда число делится на 6, тогда оно делится на 3); то, что., влечет (то, что число делится на 6, влечет то, что оно делится наЗ)и др. В то же время слова если., то могут иметь смысл знака конъюнкции & (например, в высказывании 2Гслм в планиметрии изучают плоские геометрические фигуры, то в стереометрии изучают трехмерные геометрические тела), а слову или может соответствовать по смыслу не только знак дизъюнкции V, но и знак строгой дизъюнкции (и — четное число или п — нечетное число).

Рассмотрим на примере, каким образом осуществляется такой перевод.

Во-первых, нужно выявить все элементарные высказывания, «которые входят в состав данного сложного, и различным элементарным высказываниям поставить в соответствие различные пропозициональные переменные.

Во-вторых, нужно определить логические постоянные, с помощью которых построено данное сложное высказывание. Союз о имеет здесь, очевидно, тот же смысл, какой имеет союз и, поэтому переведем его знаком конъюнкции Л. Первое или можно перевести знаком дизъюнкции V, так как песня грустная и, по-видимому, можно одновременно петь ее и глядеть задумчиво. Второе или скорее всего имеет смысл строгой дизъюнкции, так как исключается возможность одновременно смеяться и петь или задумчиво глядеть.

И наконец, в-третьих, анализируя порядок, в котором данное сложное высказывание строится из элементарных, нужно написать соответствующую ему формулу. Таким образом, в результате нашего, в известной степени произвольного, анализа текста мы можем, в конце концов, написать формулу

Осуществив настоящий перевод с естественного языка на язык логики высказываний, мы достигли того, что избавились от всей информации, которая не относится к логике, выявили логическую структуру сложного высказывания, сделали ее недвусмысленной и доступной прямому наблюдению.

----------4.3----------

ИСЧИСЛЕНИЕ ИСТИННОСТНЫХ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ФОРМУЛ

Исчисление истинностных значений логических формул осуществляется с помощью семантических таблиц для соответствующих логических союзов.

Пусть даны элементарные высказывания Я устал, Я хочу спать и Я могу заниматься, и пусть известно, что первое и третье из них истинны, а второе ложно. Что при этих условиях можно сказать о логическом значении сложного высказывания Если я устал или я хочу спать, то я не могу заниматься!

Поставим элементарным высказываниям в соответствие пропозициональные переменные p, q и г. Высказыванию Я устал или я хочу спать отвечает формула (р V q. Ищем в таблице для дизъюнкции строку, в которой р — истинно, a q — ложно, и находим, что при этих условиях формула (р V q) и соответствующее ей высказывание истинны. Поскольку интересующему нас сложному высказыванию отвечает формула

в которой антецедент имеет значение «истина», а консеквент — «ложь», то с помощью таблицы для импликации можно установить, что эта формула и все сложное высказывание имеют логическое значение «ложь».