3. Контрольні запитання

1. В чому полягає суть підстановки Віженера ?

2. В чому полягає відмінність методу Віженера від методу Цезаря?

3. Від чого залежить криптостійкість багатоалфавітних систем?

4. Яка таблиця використовується в програмі crypter.exe в якості таблиці Віженера?

5. Чи можливо провести криптоаналіз файлу, якщо нам відома частина вихідного файлу, але не відомо її розміщення ?

Лабораторна робота № 6 блочний шифр tea

Мета: дослідити роботу криптоалгоритму TEA.

Тривалість роботи – 2 години

1 Основні теоретичні відомості

1.1 Мережа Фейштеля

Мережа Фейштеля є подальшою модифікацією описаного вище методу змішування поточної частини шифруємого блоку з результатом деякої функції, обчисленої від іншої незалежної частини того ж блоку. Ця методика одержала широке поширення, оскільки забезпечує виконання вимоги про багаторазове використання ключа й матеріалу вихідного блоку інформації.

Класична мережа Фейштеля має наступну структуру:

1-ий раунд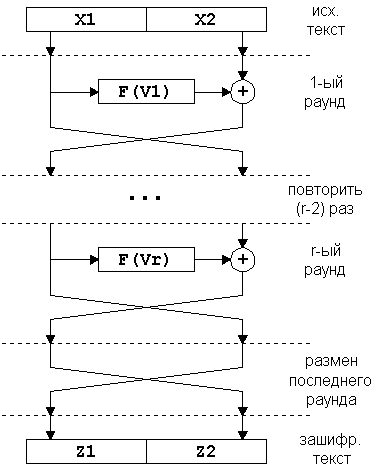

Рисунок 6.1 – Мережа Фейштеля

Незалежні потоки інформації, породжені з вихідного блоку, називаються гілками мережі. У класичній схемі їх дві. Величини V_i іменуються параметрами мережі, звичайно це функції від матеріалу ключа. Функція F називається утворюючою. Дія, що складається з однократного обчислення утворюючої функції й наступного накладення її результату на іншу галузь із обміном їх місцями, називається циклом або раундом (англ. round) мережі Фейштеля.

Оптимальне число раундів K - від 8 до 32. Важливо те, що збільшення кількості раундів значно збільшує криптостійкість будь-якого блокового шифру до криптоанализу. Можливо, ця особливість і вплинула на настільки активне поширення мережі Фейштеля - адже при виявленні, скажімо, якого-небудь слабкого місця в алгоритмі, майже завжди досить збільшити кількість раундів на 4-8, не переписуючи сам алгоритм.

Часта кількість раундів не фіксується розроблювачами алгоритму, а лише вказуються розумні межі (обов'язково нижній, і не завжди - верхній) цього параметра.

1.2 Основи алгоритму

Розглянемо один з самих простих в реалізації криптоалгоритмів - TEA (Tiny Encrypt Algoritm). Цей алгоритм включає мережу Фейштеля, в якій крім операції XOR використовується також операції арифметичного додавання та віднімання і подвійного зсуву. Так як мережа Фейштеля використовує в якості операції накладання арифметичне додавання, то вона є несиметричною (при використанні мережею Фейштеля в якості операції накладання операції виключного АБО вона є симетричною). А альтернативою є даний алгоритм (алгоритм кодування ТЕА) заснований на використанні XOR та додавання, де подвійний зсув призводить до повторного перемішування даних та бітів ключа.

1.3 Опис схеми алгоритму

Мінімальна кількість циклів, які можуть змінити одиничний біт даних -шість, але для надійного шифрування краще зробити 32 цикли (дія, що складається з однократного обчислення утворюючої функції F і наступного накладення її результату на іншу гілку з обміном їх місцями, називається циклом чи раундом (англ. round)). Схема роботи алгоритму приведена на рисунку 3.1. В даному алгоритмі ключ складається з 128 біт, що робить спробу розшифрувати дані за допомогою техніки неможливою. Дані для кодування розбиваються на дві частини Y та Z. В деяких алгоритмах ключі KEY0 та KEY1 змінювалися за допомогою додавання. Але в цьому випадку використовується змінна сума sum (її початкове значення рівне 0х00000000 в шістнадцятковій системі числення), яка утворюється арифметичним додаванням деякої константи delta в кожному циклі, що спрощує версію та робить її більш ефективною. Значення цієї константи delta= (в шістнадцятковій системі числення значення delta=0x9е3779b9). Різні частини delta використовуються в кожному циклі таким чином, що жоден біт даної частини не змінюється багатократно.

Розглянемо утворюючу функцію F, яка формується наступним чином: спочатку утворюються два доданки для операції XOR k (рис 6.2). Перший доданок формується так: значення даних Y зсувається на 4 біти вліво і арифметично додається до KEY0. Другий доданок: значення даних Y зсувається на 5 бітів вправо і арифметично додається до KEY1. Результат операції XOR k є першим доданком для операції XOR m (рис 6.1). А другий доданок для операції XOR m утворюється так: значення даних Y арифметично додається до значення sum. Утворення функції F на цьому закінчується.

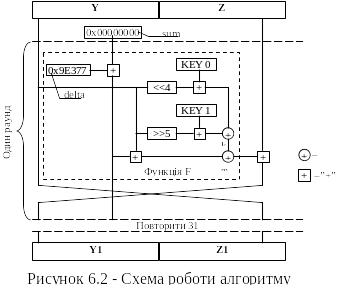
Далі значення функції F арифметично додається до значення даних Z і отримані результати Y i Z попарно міняються місцями. Далі починається наступний раунд, в якому кодується значення другої половини даних (Y).