4.3.3Отсев грубых погрешностей

Часто даже тщательно поставленные эксперименты могут давать неоднородные данные, поскольку в процессе эксперимента могут измениться условия проведения опытов. Если экспериментатор по каким-либо причинам не уловил этих изменений, наблюдения, соответствующие разным уровням факторов, будут принадлежать к разным генеральным совокупностям. Данные, соответствующие изменившимся условиям, называют грубыми погрешностями (ошибками) или резко выделяющимися (аномальными) значениями. Грубые погрешности появляются также при неправильной записи показаний приборов.

В литературе приводятся сведения о том, что экспериментальные данные могут содержать ~ 10% аномальных значений. Однако эти 10% могут дать сильное смещение при оценке параметров распределения, особенно для дисперсии, так как ошибки заметно отклоняются от основной группы значений, а на дисперсию особенно сильно влияют крайние члены вариационного ряда (вариационный ряд – результаты наблюдений, расположенные в возрастающей последовательности x₁≤ x₂≤ x₃ ... ≤ x_i …≤x_n).

В случае отсева грубых погрешностей (ошибок) нулевая гипотеза формулируется следующим образом:

Н₀ :"Среди результатов наблюдений (выборочных, опытных данных) нет резко выделяющихся (аномальных) значений ".

Альтернативной гипотезой может быть:

1) либо Н₁⁽¹⁾: "Среди результатов наблюдений есть только одна грубая ошибка",

2) либо Н₁⁽²⁾: "Среди результатов наблюдений есть две или более грубых ошибки".

В литературе можно встретить большое количество различных критериев для отсева грубых погрешностей наблюдений. Обычно экспериментаторы имеют дело с выборками небольшого объема (т.е. когда генеральная дисперсия σ_x² неизвестна и оценивается по опытным данным через выборочную дисперсию S_x²), причем именно в этом случае аномальные данные имеют большой вес. Наиболее распространенным и теоретически обоснованным в этом случае является критерий Н.В. Смирнова.

Если известно, что есть только одно аномальное значение (альтернативная гипотеза Н₁⁽¹⁾ ), то оно будет крайним членом вариационного ряда. Поэтому проверять выборку на наличие одной грубой ошибки естественно при помощи статистики:

,

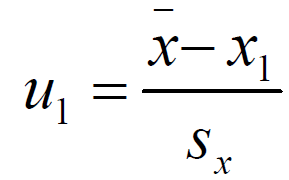если сомнение вызывает первый член вариационного ряда, , или

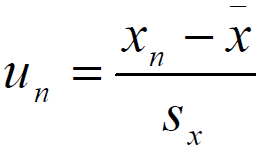
если сомнителен максимальный член вариационного ряда .

При этом, среднее значение параметра вычисляется по формуле:

,

где - число наблюдений.

Среднеквадратическое отклонение вычисляется по формуле:

или

При выбранном уровне значимости α критическая область для критерия Н.В. Смирнова строится следующим образом:

u₁ > u_α,n или u_n > u_α,n .

где u_α,n – это табличные значения (Таблица 6).

В случае если выполняется последнее условие (статистика попадает в критическую область), то нулевая гипотеза отклоняется, т.е. выброс x₁ или x_n не случаен и не характерен для рассматриваемой совокупности данных, а определяется изменившимися условиями или грубыми ошибками при проведении опытов. В этом случае значение x₁ или x_n исключают из рассмотрения, а найденные ранее оценки подвергаются корректировке с учетом отброшенного результата.

Пример. Пирометром измеряется температура поверхности нагретого тела. Было проведено шесть измерений температуры T °С, и получены следующие значения: 925, 930, 950, 975, 990, 1080 (n = 6, причем, как видно, все значения приведены в возрастающей последовательности, т.е. в виде вариационного ряда T₁=925 ≤ T₂=930 ≤ T₃ =950... ≤T₆=1080). Можно ли значение T₆=1080 считать грубой погрешностью, полученной, допустим, в результате неправильной регистрации показаний пирометра?

Таблица 6 - Критические значения критерия Н.В. Смирнова в зависимости от объема выборки n и уровня значимости α

n
	a=0.10	a=0,05	a=0,01
3	1.15	1,15	1,15
4	1,42	1,46	1,49
5	1,60	1-67	1.75
6	1,73	1,82	1,94
7	1,83	1,94	2,10
8	1,91	2,03	2,22
9	1,98	2,11	2,32
10	2,03	2,18	2,41
11	2,09	2,23	2,48
12	2,13	2,29	2,55
13	2,17	2,33	2,61
14	2,21	2,37	2,66
15	2,25	2,41	2,70
16	2,28	2,44	2,75
17	2,31	2,48	2,78
18	2,34	2,50	2,82
19	2,36	2,53	2,85
20	2,38	2,53	2,88
21	2,41	2,58	2,91
22	2,43	2,60	2,94
23	2,45	2,62	2,96
24	2,47	2,64	2,99
25	2,49	2,66	3,01

Для ответа на поставленный в этом примере вопрос предварительно вычислим оценки параметров распределения исследуемой случайной величины T (предполагая, что она не противоречит нормальному закону распределения): выборочное среднее арифметическое и выборочное среднее квадратичное отклонение S_T:

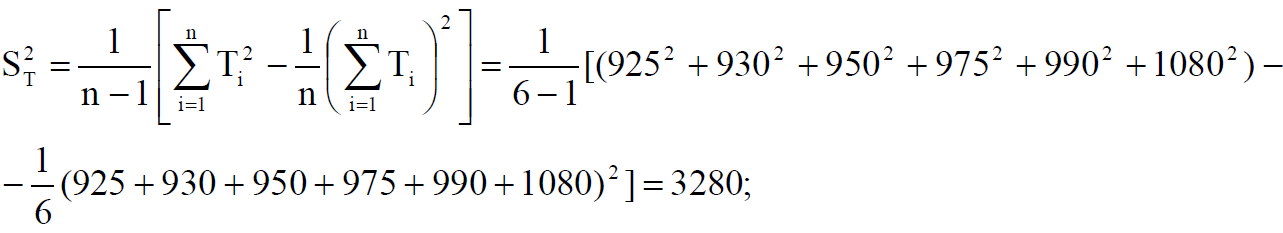
Теперь воспользуемся предложенным выше алгоритмом проверки стати­стических гипотез.

1. Формулируем нулевую гипотезу Н₀: "Среди значений 925; 930: 950; 975; 990: 1080 нет грубых погрешностей".

2. Исходя из условий примера выбираем следующую альтернативную ги­потезу Н₁⁽¹⁾: "Значение 1080 является (одной) грубой погрешностью".

3. Сформулированная нулевая гипотеза Н₀ может быть проверена по критерию Н.В. Смирнова.

4. Значение статистики критерия Н.В. Смирнова равно:

5. Уровень значимости α примем равным 0,05.

6. По Таблица 6 при α = 0,05 и n = 6 находим u_0,05;6 = 1,82, и строим критическую область ω: u₆ > u_0,05;6, т.е. u₆ > 1,82.

7. Принимаем решение: поскольку значение статистики (1,83 > 1,82) попало в критическую область – нулевая гипотеза отвергается, и в качестве рабочей принимается альтернативная гипотеза, т.е. значение 1080 с вероятностью 0,95 (уровень значимости, не превышает 0,05) по критерию Н.В. Смирнова можно считать грубой погрешностью. Интересно отметить, что если бы на этапе 5 мы приняли α = 0,01, по таблицам критерия Н.В. Смирнова u_0,01;6 = 1,94 и подсчитанное значение статистики при этом уровне значимости, то оно не попало бы в критическую область (1,83<1,94). Следовательно, при α = 0,01 мы не можем отвергнуть нулевую гипотезу, т.е. по критерию Н.В. Смирнова с вероятностью 0,99 (надежностью, достоверностью) мы не можем сказать, что значение 1080 является грубой погрешностью.