
- •14. Личность испытуемого и ситуация психологического эксперимента.
- •15. Основные виды экспериментов.
- •1.В зависимости от способа проведения
- •2.В зависимости от результата воздействия выделяют
- •3.В зависимости от этапа исследования
- •4. В зависимости от уровня осознанности
- •16. Цели, задачи и особенности констатирующего и формирующего экспериментов.
- •17. Основные экспериментальные планы.
- •18. Доэкспериментальные и квазиэкспериментальные планы.
- •1 Доэкспериментальные планы
- •2 Квазиэкспериментальные планы
- •19. Факторные экспериментальные планы.
- •20. Корреляционное исследование.
- •21. Этапы психологического экспериментального исследования
- •22. Проблема исследования. Противоречие как основа проблемы исследования.
- •23. Гипотезы экспериментального исследования. Виды гипотез.
- •24. Валидность: внутренняя, внешняя и операциональная.
19. Факторные экспериментальные планы.
Факторные
экспериментальные планы
Применяются
для проверки сложных гипотез о взаимосвязях
между переменными. В факторном эксперименте
проверяются, как правило, два типа
гипотез: 1) гипотезы о раздельном влиянии
каждой из независимых переменных; 2)
гипотезы о взаимодействии переменных.
Факторный план заключается в том, чтобы
все уровни независимых переменных
сочетались друг с другом. Число
экспериментальных групп при этом равно
числу сочетаний.
^
Факторный
план для двух независимых переменных
и двух уровней
(2 х 2). Это наиболее простой из факторных
планов. Его схема выглядит так
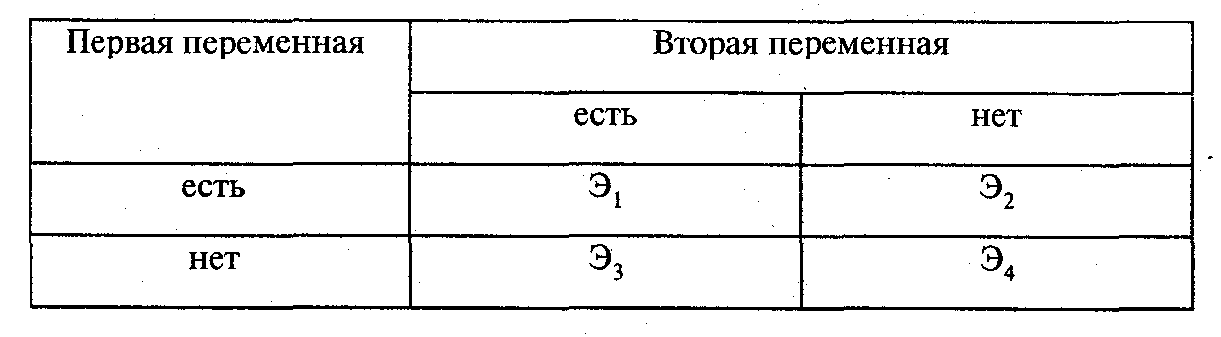 Данный
план выявляет эффект воздействия двух
независимых переменных на одну зависимую.
Экспериментатор сочетает возможные
переменные и уровни. Иногда используются
четыре независимые рандомизированные
экспериментальные группы, Для обработки
результатов применяется дисперсионный
анализ по Фишеру.
Существуют более
сложные версии факторного плана: З х 2
и З х З и т.д. Дополнение каждого уровня
независимой переменной увеличивает
число экспериментальных групп.
Латинский
квадрат.
Является упрощением полного плана для
трех независимых переменных, имеющих
два и более уровней. Принцип латинского
квадрата состоит в том, что два уровня
разных переменных встречаются в
экспериментальном плане только один
раз. Тем самым значительно сокращаются
количество групп и экспериментальная
выборка в целом.
Например, для
трех независимых переменных (L, М, N) с
тремя уровнями у каждой (1, 2, 3 и N(А, В, С))
план по методу «латинского квадрата»
будет выглядеть так.
Данный
план выявляет эффект воздействия двух
независимых переменных на одну зависимую.
Экспериментатор сочетает возможные
переменные и уровни. Иногда используются
четыре независимые рандомизированные
экспериментальные группы, Для обработки
результатов применяется дисперсионный
анализ по Фишеру.
Существуют более
сложные версии факторного плана: З х 2
и З х З и т.д. Дополнение каждого уровня
независимой переменной увеличивает
число экспериментальных групп.
Латинский
квадрат.
Является упрощением полного плана для
трех независимых переменных, имеющих
два и более уровней. Принцип латинского
квадрата состоит в том, что два уровня
разных переменных встречаются в
экспериментальном плане только один
раз. Тем самым значительно сокращаются
количество групп и экспериментальная
выборка в целом.
Например, для
трех независимых переменных (L, М, N) с
тремя уровнями у каждой (1, 2, 3 и N(А, В, С))
план по методу «латинского квадрата»
будет выглядеть так.
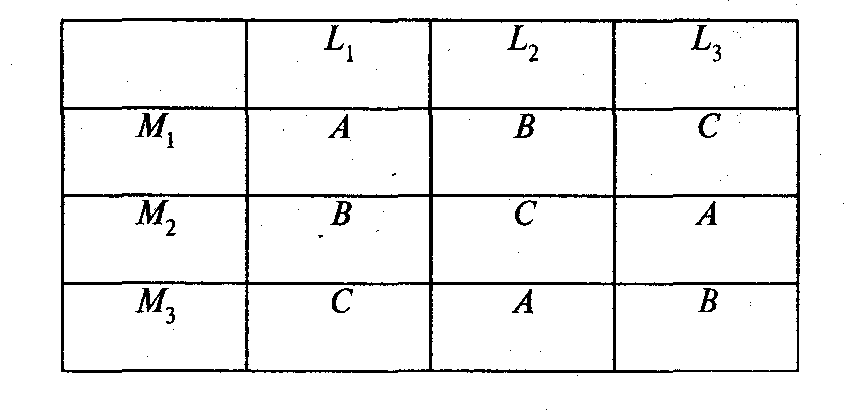 В
этом случае уровень третьей независимой
переменной (А, В, С) встречается в каждой
строке и в каждой колонке по одному
разу. Комбинируя результаты по строкам,
столбцам и уровням, можно выявить влияние
каждой из независимых переменных на
зависимую, а также степень попарного
взаимодействия переменных. Применение
латинских букв А, В, С для обозначения
уровней третьей переменной традиционно,
поэтому метод и получил название
«латинский квадрат».
«Греко-латинский
квадрат». Этот план применяется в случае,
если необходимо исследовать влияние
четырех независимых переменных. Он
строится на основе латинского квадрата
для трех переменных, при этом к каждой
латинской группе плана присоединяется
греческая буква, обозначающая уровни
четвертой переменной. Схема для плана
с четырьмя независимыми переменными,
каждая из которых имеет три уровня,
будет выглядеть так:
В
этом случае уровень третьей независимой
переменной (А, В, С) встречается в каждой
строке и в каждой колонке по одному
разу. Комбинируя результаты по строкам,
столбцам и уровням, можно выявить влияние
каждой из независимых переменных на
зависимую, а также степень попарного
взаимодействия переменных. Применение
латинских букв А, В, С для обозначения
уровней третьей переменной традиционно,
поэтому метод и получил название
«латинский квадрат».
«Греко-латинский
квадрат». Этот план применяется в случае,
если необходимо исследовать влияние
четырех независимых переменных. Он
строится на основе латинского квадрата
для трех переменных, при этом к каждой
латинской группе плана присоединяется
греческая буква, обозначающая уровни
четвертой переменной. Схема для плана
с четырьмя независимыми переменными,
каждая из которых имеет три уровня,
будет выглядеть так:
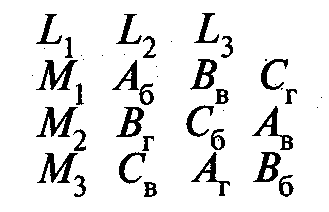 Для
обработки данных, полученных в плане
«греко-латинский квадрат», применяется
метод дисперсионного анализа по
Фишеру.
Главная проблема, которую
позволяют решить факторные планы,
определение взаимодействия двух и более
переменных. Эту задачу невозможно
решить, применяя несколько обычных
экспериментов с одной независимой
переменной. В факторном плане вместо
попыток «очистить» экспериментальную
ситуацию от дополнительных переменных
(с угрозой для внешней валидности)
экспериментатор приближает ее к
реальности, вводя некоторые дополнительные
переменные в разряд независимых. При
этом анализ связей между изучаемыми
признаками позволяет выявить скрытые
структурные факторы, от которых зависят
параметры измеряемой переменной.
Для
обработки данных, полученных в плане
«греко-латинский квадрат», применяется
метод дисперсионного анализа по
Фишеру.
Главная проблема, которую
позволяют решить факторные планы,
определение взаимодействия двух и более
переменных. Эту задачу невозможно
решить, применяя несколько обычных
экспериментов с одной независимой
переменной. В факторном плане вместо
попыток «очистить» экспериментальную
ситуацию от дополнительных переменных
(с угрозой для внешней валидности)
экспериментатор приближает ее к
реальности, вводя некоторые дополнительные
переменные в разряд независимых. При
этом анализ связей между изучаемыми
признаками позволяет выявить скрытые
структурные факторы, от которых зависят
параметры измеряемой переменной.
