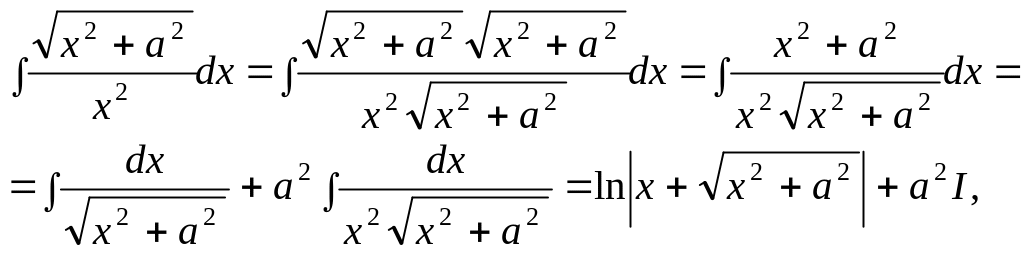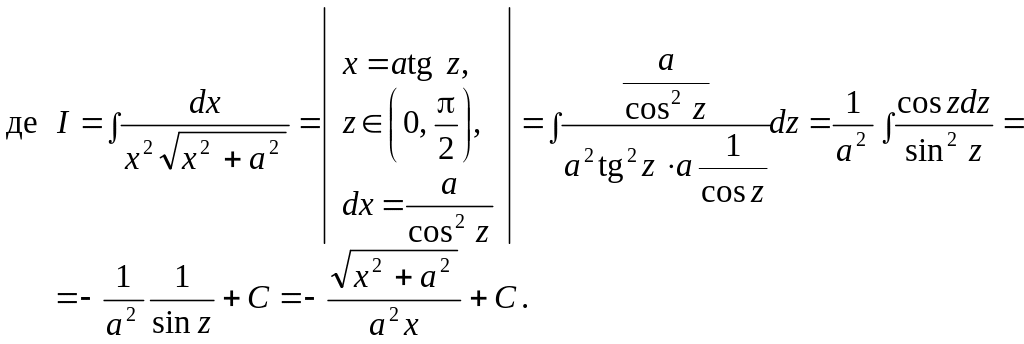- •6.1.1. Поняття невизначеного інтеграла
- •6.1.2. Основні властивості невизначеного інтеграла
- •Закінчення табл.
- •Робоча формула
- •Узагальнена формула інтегрування частинами:
- •1. Інтегрування основних простих дробів
- •Стислі відомості про алгебраїчні рівняння
- •Тотожна рівність двох многочленів
- •Розклад многочлена з дійсними коефіцієнтами
- •6. Розклад правильного раціонального дробу на найпростіші
- •6.1.7. Інтегрування раціональних дробів: інший підхід
- •Властивості раціональних функцій
- •6.1.8. Інтегрування ірраціональних виразів
- •6.1.9. Біноміальний диференціал
- •6.1.10. Інтегрування тригонометричних виразів
6.1.8. Інтегрування ірраціональних виразів
Інтеграли від ірраціональних функцій за допомогою підстановок, які залежать від типу підінтегральних виразів, зводяться до інтегралів від раціональних функцій.
Розглянемо основні типи ірраціональних підінтегральних виразів та підстановки, за якими вони раціоналізуються.
1.
![]()
![]()

2 .
![]()
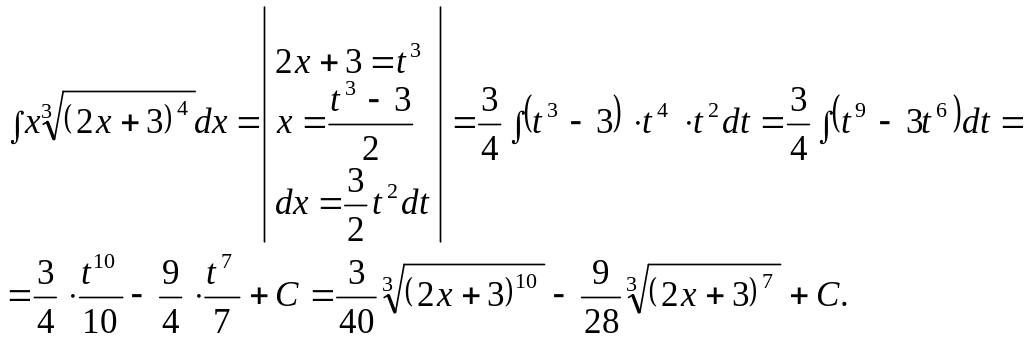
3 .
![]()
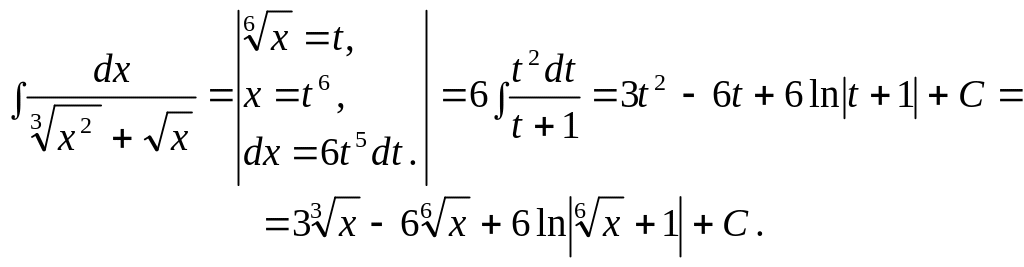
4 .


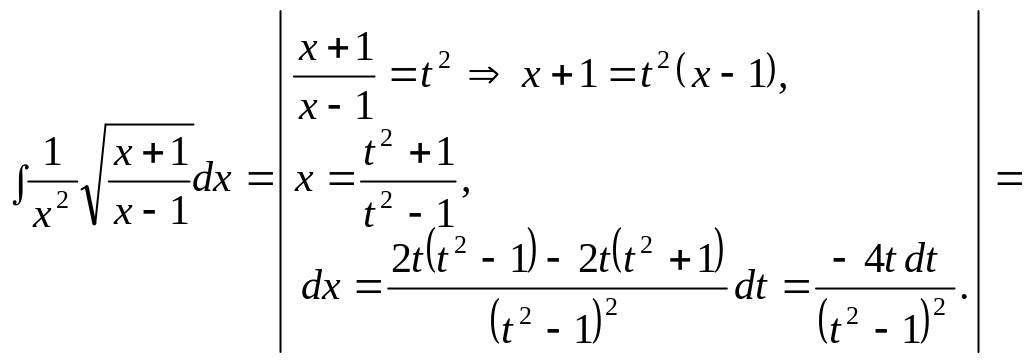
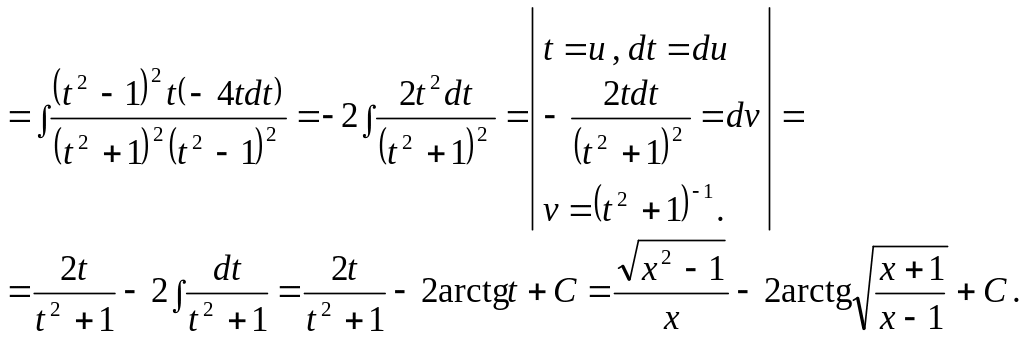
5 .1.
.1.
![]()
5.2.
![]()
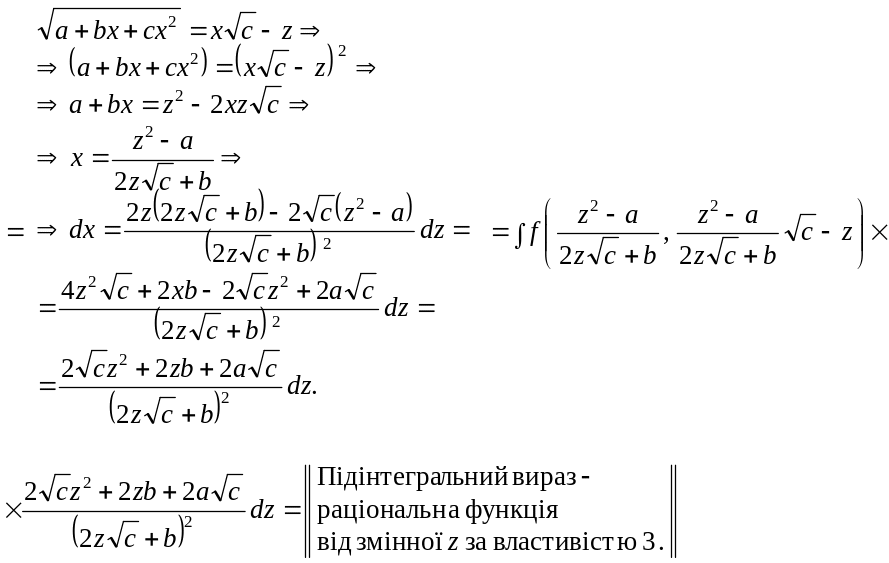

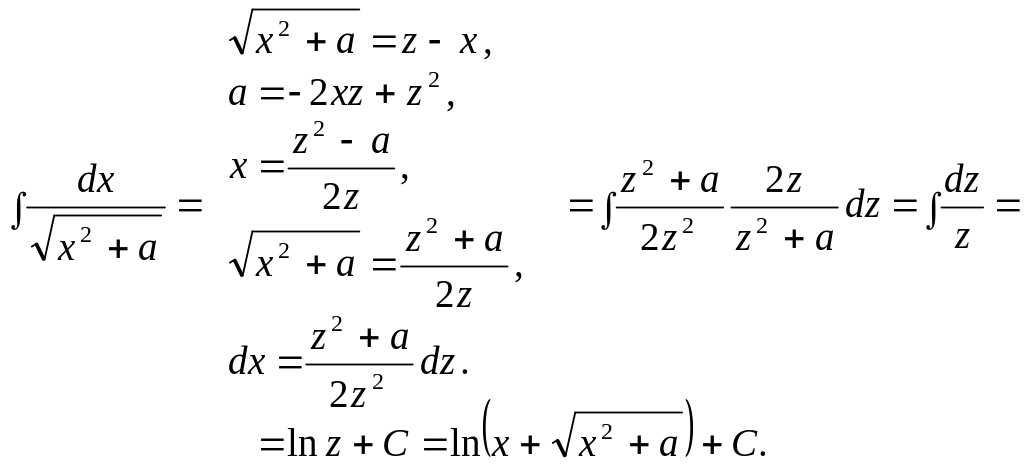

6 .
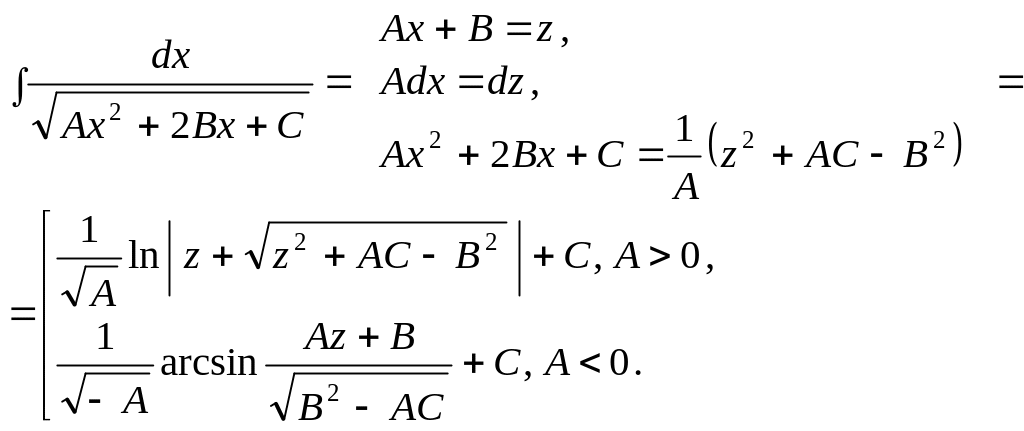

7 .


де
![]()
![]()
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
![]()
8 .
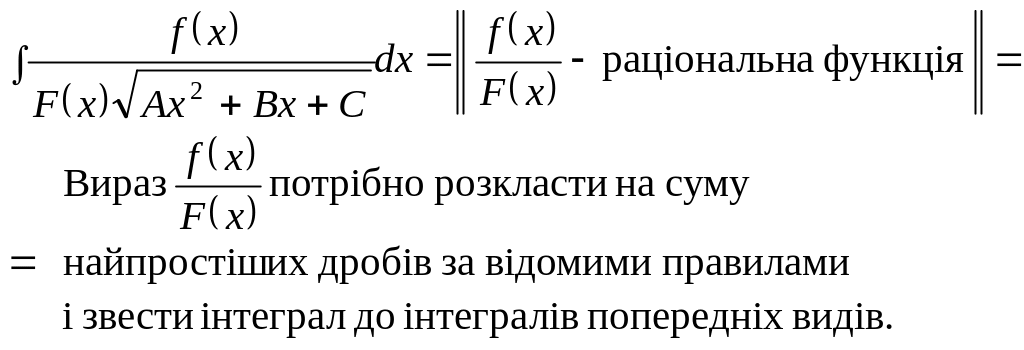

1)
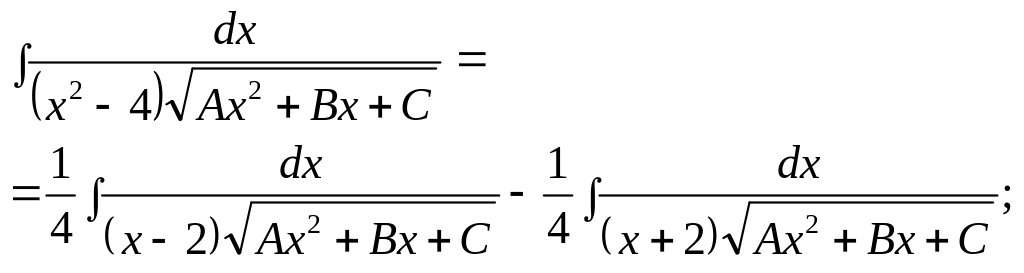
2)
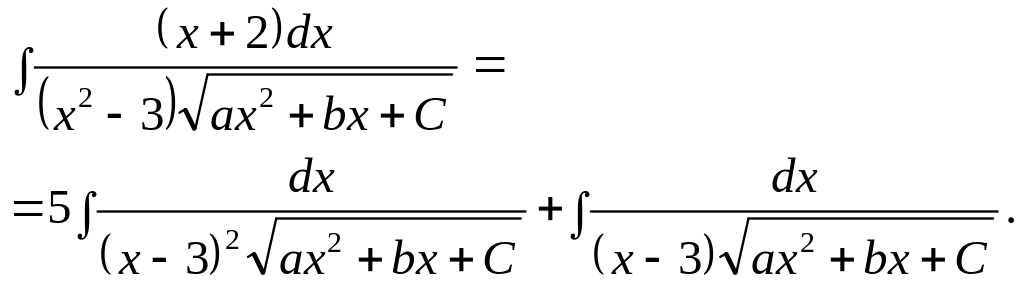
1)
![]()
2)
![]()
3)
![]()
4
)
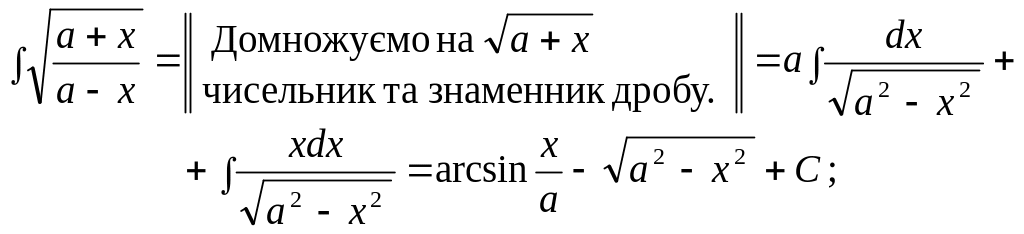
9.
Підстановки Ейлера, за допомогою яких
завжди раціоналізується вираз виду
![]() ,
де
,
де
![]() — раціональна функція.
— раціональна функція.
Перша
підстановка
![]() :
:
![]() .
.
Друга
підстановка
![]() :
:
![]() .
.
Третя
підстановка
![]() :
:
![]() або
або
![]() .
.
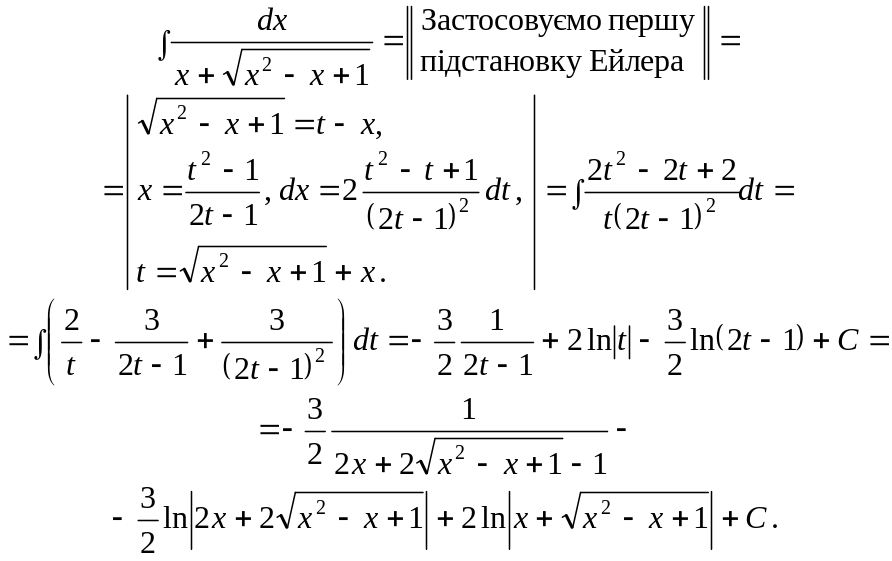
10.
Виокремити алгебраїчну частину з
інтеграла
![]() ,
де
— многочлен
,
де
— многочлен
![]() -го
степеня, можна за формулою
-го
степеня, можна за формулою
![]() (32)
(32)
де
— многочлен n-го
степеня,
![]() Коефіцієнти цього многочлена
знайдемо за методом невизначених
коефіцієнтів. Продиференціювавши (32) і
помноживши здобуту рівність на
Коефіцієнти цього многочлена
знайдемо за методом невизначених
коефіцієнтів. Продиференціювавши (32) і
помноживши здобуту рівність на
![]() ,
дістанемо:
,
дістанемо:
![]() (33)
(33)
Звідси методом невизначених коефіцієнтів знайдемо .

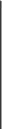
![]()
6.1.9. Біноміальний диференціал
Означення. Вираз виду
![]() (34)
(34)
де
![]() і
і
![]() — сталі показники,
— сталі показники,
![]() — раціональні числа, називається
біноміальним
диференціалом.
— раціональні числа, називається
біноміальним
диференціалом.
Диференціал (34) введенням нової змінної можна перетворити на диференціал такого самого виду, але з цілими показниками.
● Справді,
беручи
![]() дістаємо
дістаємо
![]()
Узявши
![]() так, щоб
так, щоб
![]() і
і
![]() були цілими, знайдемо біноміальний
диференціал з цілими показниками.
були цілими, знайдемо біноміальний
диференціал з цілими показниками.
Далі
з тотожності
![]() випливає, що диференціал (34) може бути
перетворений на диференціал
типу
випливає, що диференціал (34) може бути
перетворений на диференціал
типу
![]() ,
але до нього замість
входить –n,
а отже,
в одному з двох диференціалів показник
буде додатним. Таким чином, не порушуючи
загальності, можемо вважати, що
,
але до нього замість
входить –n,
а отже,
в одному з двох диференціалів показник
буде додатним. Таким чином, не порушуючи
загальності, можемо вважати, що
![]() і
— цілі числа і
—
додатне.
і
— цілі числа і
—
додатне.
Т ри
випадки інтегровності у скінченному
вигляді
біноміальних диференціалів
(34)
ри
випадки інтегровності у скінченному
вигляді
біноміальних диференціалів
(34)
І. — ціле число. Тоді диференціал (34) — раціональна функція.
ІІ.
![]() Тоді диференціал (34) заміною
Тоді диференціал (34) заміною
![]() перетворюється
на раціональну функцію.
перетворюється
на раціональну функцію.
● 

![]()
ІІІ.
![]() Тоді, застосувавши заміну
Тоді, застосувавши заміну
![]() до виразу
до виразу
![]() дістанемо:
дістанемо:
●
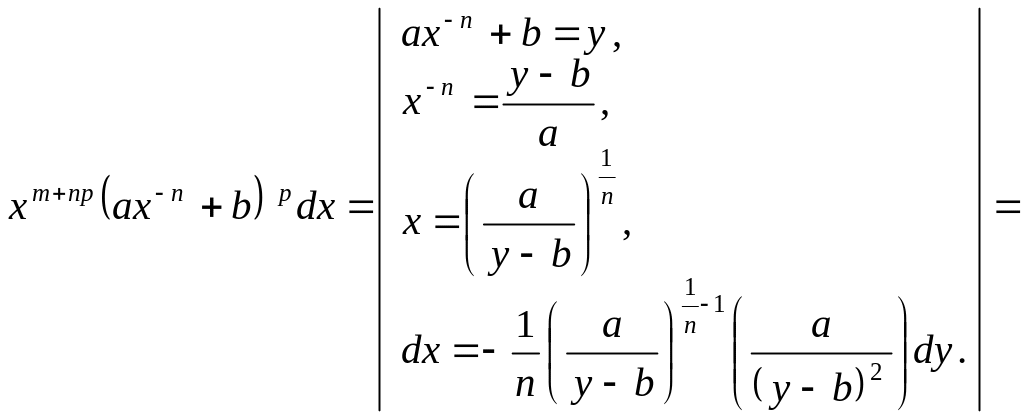
![]()
![]()
Ці випадки інтегровності були відомі ще Ньютонові. Але лише П. Л. Чебишов встановив, що інших випадків інтегровності у скінченному вигляді для біноміальних диференціалів не існує.
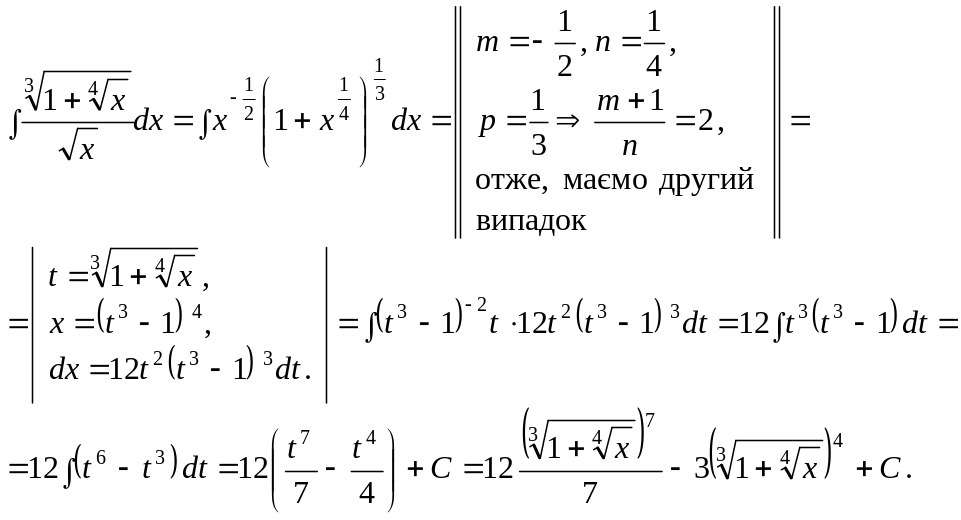
У разі, якщо
![]() ,
а p, q
— цілі числа, для обчислення інтегралів
від біноміального диференціала можна
застосувати формули зведення.
,
а p, q
— цілі числа, для обчислення інтегралів
від біноміального диференціала можна
застосувати формули зведення.
Інтеграл
![]() можна звести до інтегралів
можна звести до інтегралів
![]() або
або
![]() :
:
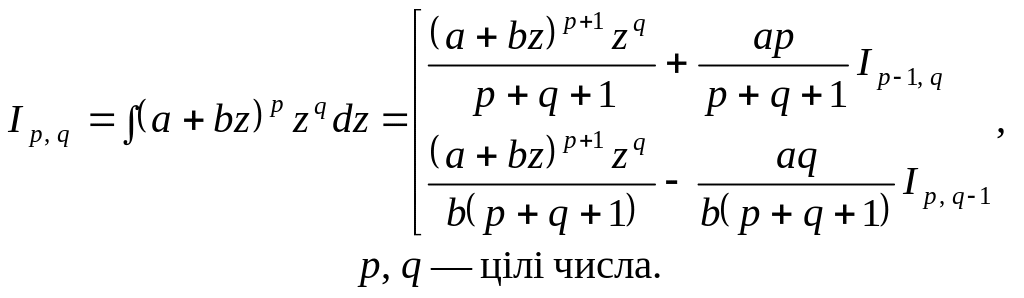
6.1.10. Інтегрування тригонометричних виразів
Розглянемо деякі підстановки, що раціоналізують інтеграл від тригонометричного виразу
![]()
де
![]() — раціональна функція від
— раціональна функція від
![]()
І.
Універсальна
підстановка
![]()
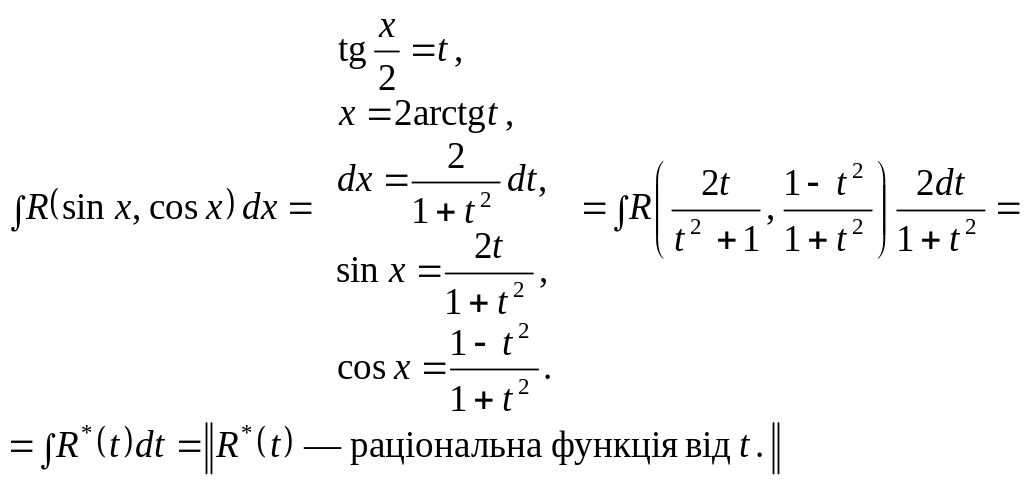

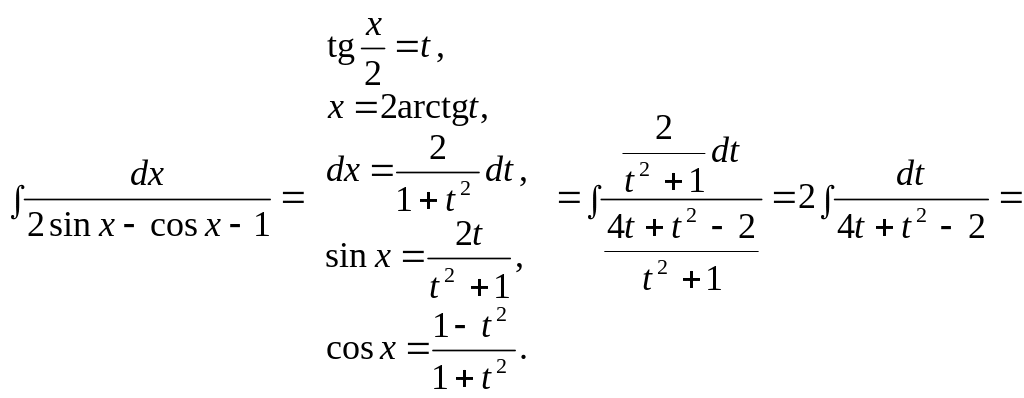

В окремих випадках можна користуватися простішими підстановками.
ІІ. Якщо інтеграл зводиться до виду
![]() ,
,
то
застосовуємо заміну
![]()
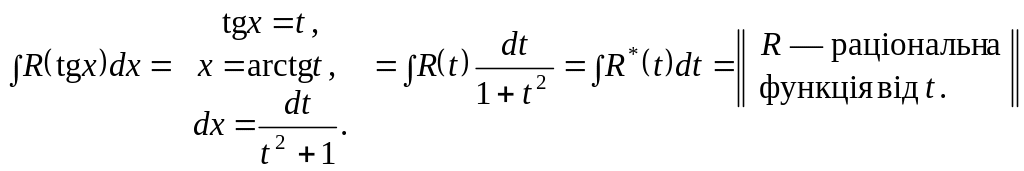

Із
цим випадком стикаємося щоразу, коли
підінтегральний вираз містить парні
степені
![]() і
і
![]() оскільки
оскільки
![]() ,
,
![]() .
.
ІІІ. Якщо інтеграл зводиться до виду
![]() ,
,
то
виконуємо заміну
![]()
![]()
ІV. Якщо інтеграл зводиться до виду
![]()
то
виконуємо підстановку
![]()
![]() .
.
V. Якщо інтеграл зводиться до виду
![]()
де
![]() — цілі
числа,
то
підінтегральний
диференціал
є
раціональна
функція
від
— цілі
числа,
то
підінтегральний
диференціал
є
раціональна
функція
від
![]() і
і
![]() ,
яку
можна
зінтегрувати
відомими
методами.
,
яку
можна
зінтегрувати
відомими
методами.
![]()
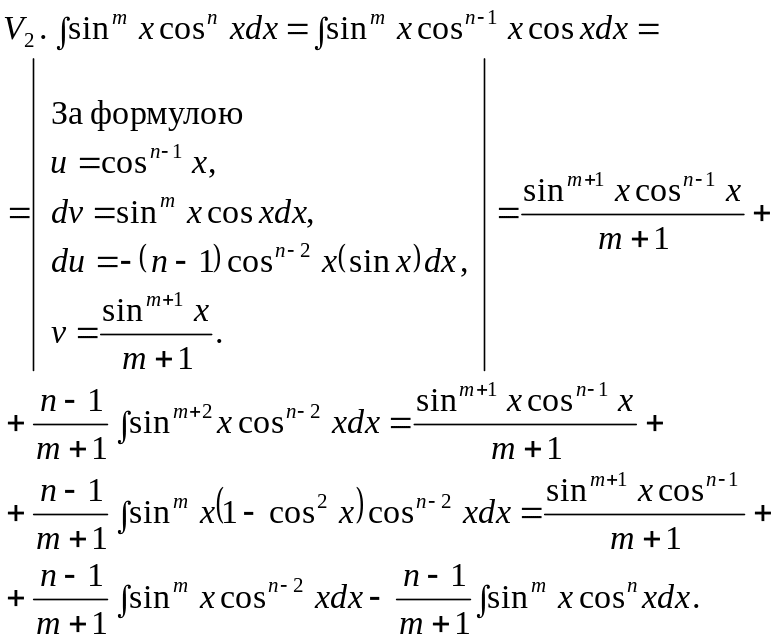
Розв’язуючи здобуте рівняння відносно даного інтеграла, дістаємо:
![]()
VI. Деякі підінтегральні вирази, що зводяться до раціонального вигляду підстановками 1—4, можуть бути безпосередньо знайдені за допомогою штучних прийомів.
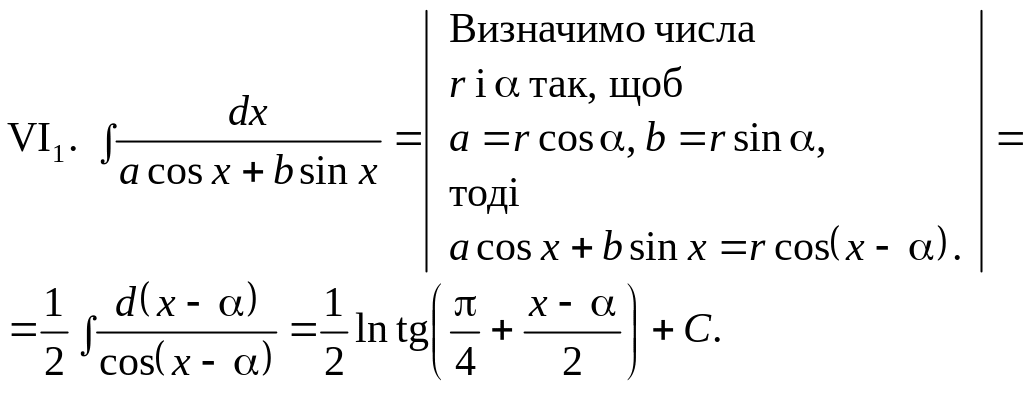
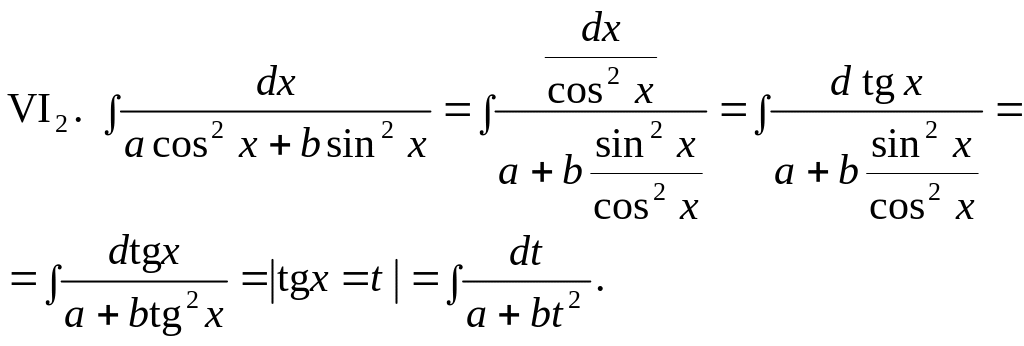
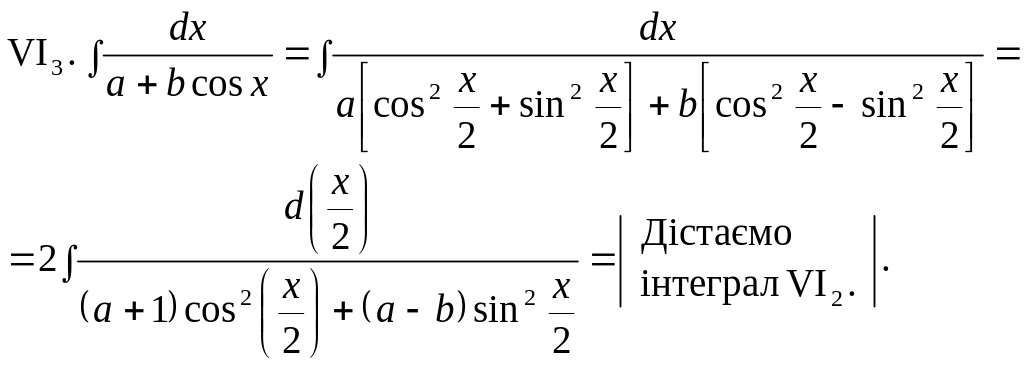
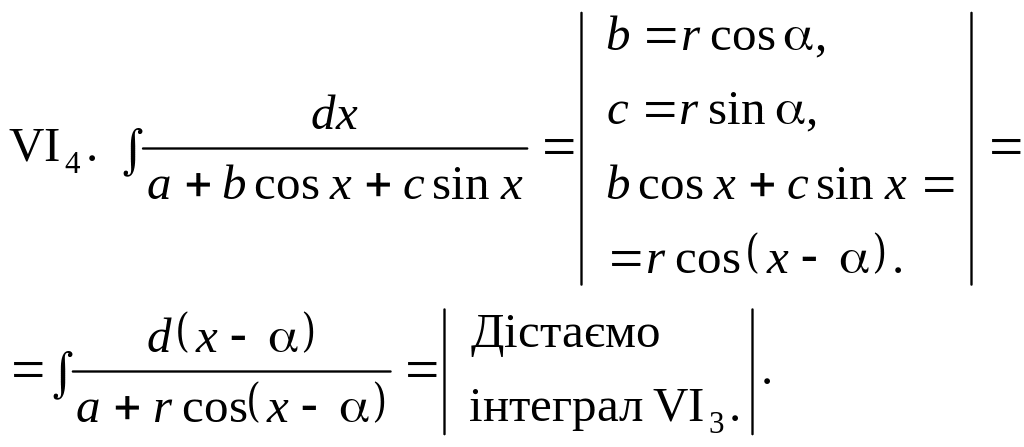
Тригонометричні підстановки для раціоналізації ірраціональних виразів
Інтегруючи
вирази виду
![]() або
або
![]() ,
найчастіше користуються такими
підстановками:
,
найчастіше користуються такими
підстановками:
для
виразів, що містять
підстановкою
![]() або
або
![]()
для
виразів, що містять
![]() підстановкою
підстановкою
![]() або
або
![]()
для
виразів, що містять
![]() підстановкою
підстановкою
![]() або
або
![]()
1. 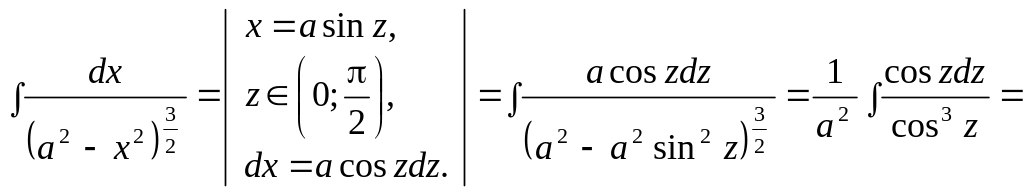
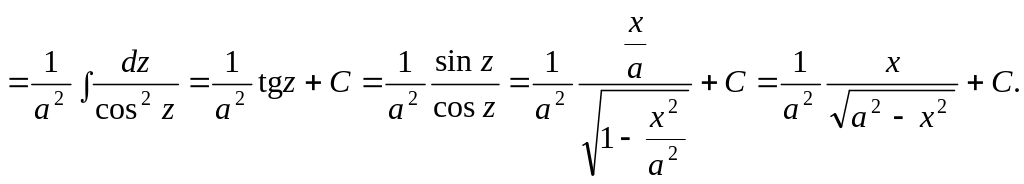
2.