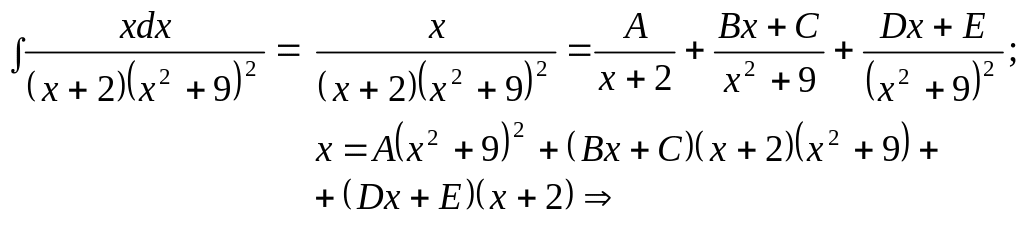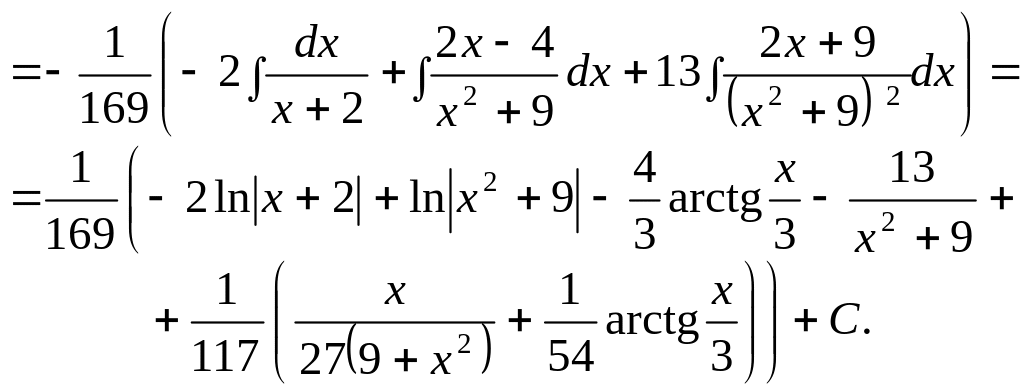Стислі відомості про алгебраїчні рівняння

Теорема (Безу). При діленні многочлена на остача від ділення дорівнює .

Доведення. Поділивши на , дістанемо частку і остачу

Звідси

Нехай , тоді

Д ано

Поділимо на

Отже, . Водночас за теоремою Безу .

Наслідок. Для того, щоб многочлен ділився без остачі на , необхідно і достатньо, щоб

Сформулюємо без доведення основну теорему алгебри, автором якої є К. Гаусс.

Теорема. Будь-який алгебраїчний многочлен при має дійсний (або комплексний) корінь.

З теореми Гаусса випливає, що кожний многочлен n-го степеня можна розкласти на множники:

,

де — корені цього многочлена.

Тотожна рівність двох многочленів

Розглянемо два многочлени n-го степеня:

,

.

Означення. Якщо тобто всі відповідні коефіцієнти многочленів рівні між собою, то говорять, що многочлени і тотожно рівні між собою. Записують: .

Теорема. Якщо , то відповідні коефіцієнти много- членів однакові:

.

Теорема. Якщо значення двох многочленів n-го степеня збігаються в точці, то многочлени тотожно рівні між собою.

Розклад многочлена з дійсними коефіцієнтами

Теорема. Якщо многочлен з дійсними коефіцієнтами має комплексний корінь , то він має і комплексно спряжений корінь .

Візьмемо довільний многочлен з дійсними коефіцієнтами й розкладемо його на лінійні множники:

.

Серед коренів можуть бути дійсні та комплексні. Згрупувавши однакові корені, дістанемо:

де — дійсні корені многочлена ; — цілі числа, так зва- ні кратності коренів многочлена; — цілі числа, так звані крат- ності квадратних тричленів; — дійсні числа. При цьому , де n — степінь многочлена .

6. Розклад правильного раціонального дробу на найпростіші

Теорема 2.3. Якщо — правильний раціональний дріб, то його можна записати у вигляді:

,

де всі дроби є правильними.

Теорема 2.4. Правильний раціональний дріб

у разі, якщо не ділиться на , можна подати у вигляді:

Теорема (Ейлера). 2.5. Нехай — правильний раціональний дріб, знаменник якого записано в зазначеному щойно вигляді, тоді цей дріб можна єдиним чином подати як суму найпростіших дробів:

Наведений вираз називається розкладом раціонального дробу на найпростіші дроби.

Для визначення невідомих коефіцієнтів існують кілька способів.

Рівність між многочленом у лівій частині і многочленом у правій частині має виконуватися для всіх , тому коефіцієнти при однакових степенях в обох частинах мають збігатися. Зрівнюючи їх, дістаємо систему лінійних алгебраїчних рівнянь відносно невідомих коефіцієнтів. Цей метод знаходження коефіцієн­тів розкладу правильного раціонального дробу на суму найпрос­тіших дробів називається методом невизначених коефіцієнтів.

^● Зведемо ліву і праву частини до спільного знаменника:

1. Якщо містить лінійних множників, то, підставляючи в обидві частини останньої рівності замість х значення відповідних коренів, знайдемо коефіцієнти:

2. Підставивши в обидві частини цієї ж рівності замість х певні значення (наприклад, отримаємо систему алгебраїчних рівнянь, розв’язавши яку знайдемо коефіці- єнти Інший шлях: коефіцієнти знайдемо методом невизначених коефіцієнтів. Потрібно розкрити дужки, звести подібні члени й розв’язати утворену систему рівнянь.

З найти .

^●

Розкладаємо спочатку підінтегральний дріб на прості дроби за теоремою 2.5

Коефіцієнт знайдемо підставлянням значення кореня :

Коефіцієнти знайдемо методом невизначених коефіцієнтів:

Степені

Рівності, отримані при порівнянні коефіцієнтів при відповідних степенях

З найти ^.

^●

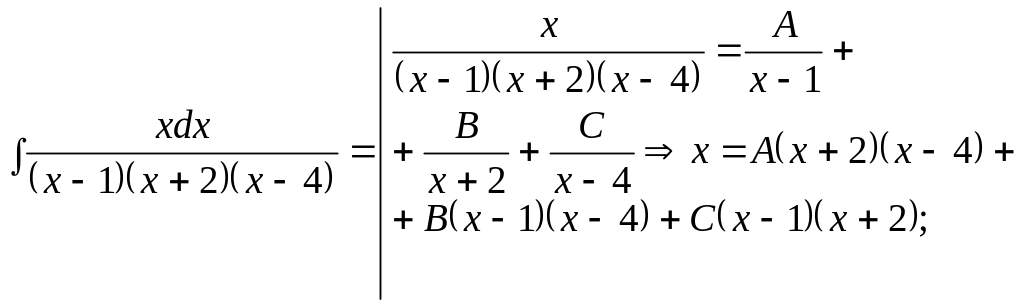
З найти .

^