3.4.5. Гіпербола

Означення. Канонічним рівнянням гіперболи називаються рівняння

(1)

Ця крива розміщена симетрично відносно осей х та у. Початок координат є центром симетрії гіперболи. З рівняння

випливає, що .

1. Гіпербола утворена двома вітками, які містяться в області

.

 Справді, з рівняння (1) маємо:

.

Область, в якій розміщені вітки гіперболи, обмежені прямими	(2)
,
які називаються асимптотами гіперболи.

З рівняння

бачимо, що узростає зі зростанням х при (рис. 3.46).

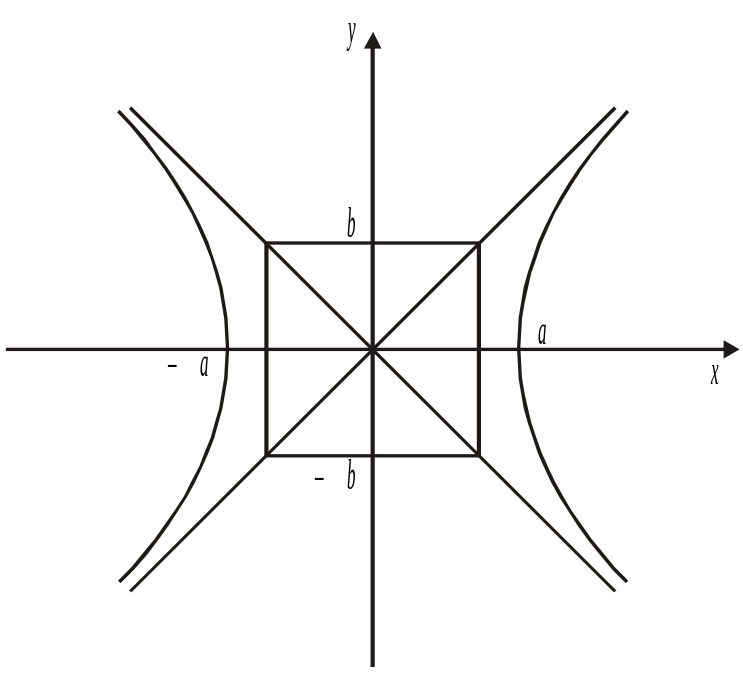
Рис. 3.46

2. Розглянемо вітку гіперболи, яка визначається рівнянням

,

і доведемо, що при ця вітка наближається до асимптоти з рівнянням .

 Справді, маємо такі співвідношення:

.

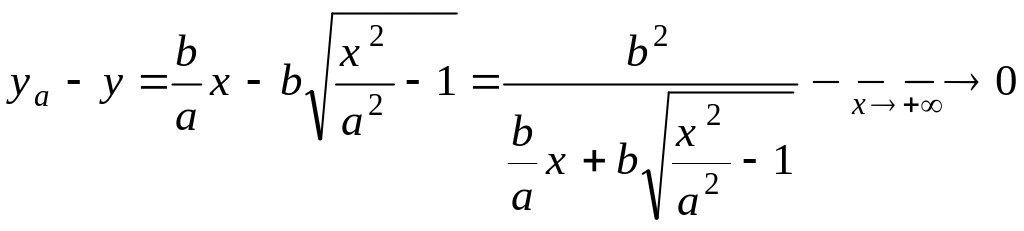Багато властивостей гіперболи аналогічні властивостям еліпса.

Означення. Пряма, що проходить через центр симетрії гіперболи, називається її діаметром. Центри всіх хорд гіперболи, що мають рівняння

,

лежать на діаметрі гіперболи, який подається рівнянням .

Діаметри гіперболи

(3)

називаються спряженими. Хорди гіперболи, паралельні одному й тому самому діаметру, поділяються спряженим діаметром пополам. Якщо дотична до гіперболи паралельна деякому діаметру, то спряжений діаметр проходить через точку дотику.

Рівняння дотичної до гіперболи в точці М₀(х₀, у₀) подається у вигляді

. (4)

3. Знайдемо ексцентриситет гіперболи, скориставшись рівнянням (1). Для цього візьмемо

.

Остаточно при маємо:

,

або

(5)

З найдемо ексцентриситет гіперболи

.

 Маємо: . 

4. Доведемо фокальну властивість гіперболи, яка може використовуватися для означення гіперболи.

Означення. Гіперболою називається геометричне місце точок, різниця відстаней яких до двох даних точок, що називаються фокусами, є величина стала.

Відстань між фокусами дорівнює 2с. Проведемо вісь х через фокуси і припустимо, що вісь у поділяє відрізок між фокусами пополам (рис. 3.47).

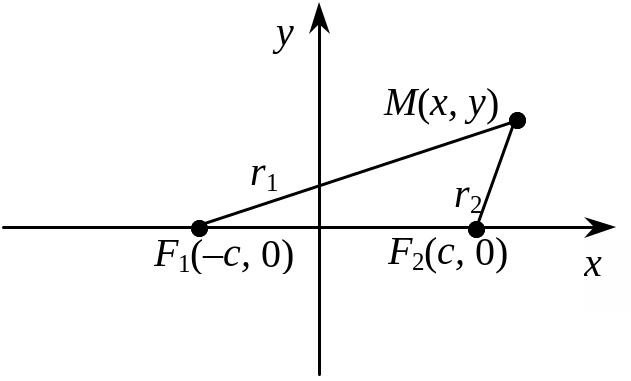
Рис. 3.47

Візьмемо

або

. (6)

Тут знак «+» для правої вітки гіперболи, а знак «–» — для лівої.

Перетворимо це рівняння гіперболи, позбавившись від ірраціональності:

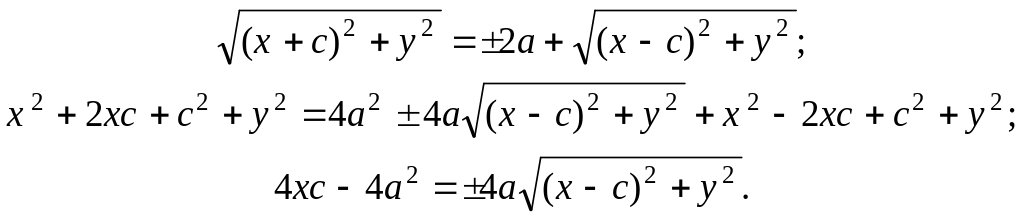
Отже,

(7)

Звідси:

Остаточно:

Роблячи заміну , дістаємо відоме канонічне рівняння гіперболи.

Рівняння (7) можна подати у вигляді

(8)

Знак «+» відповідає правій вітці гіперболи, знак «–» — лівій.

5. Доведемо, що прямі є директрисами гіперболи (рис. 3.48).

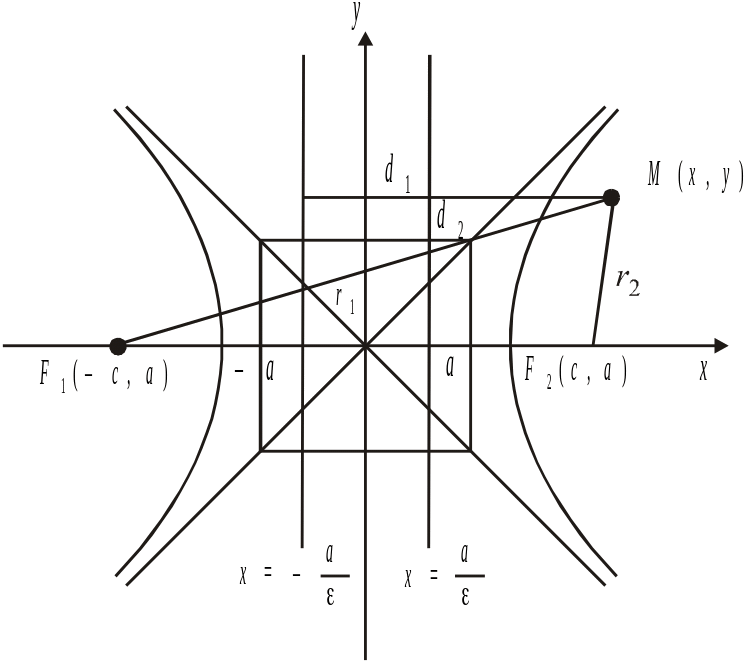
Рис. 3.48

Для довільної точки на правій вітці гіперболи М(х, у) маємо:

.

Обчислюємо відношення фокальних радіусів до відстаней директрис:

.

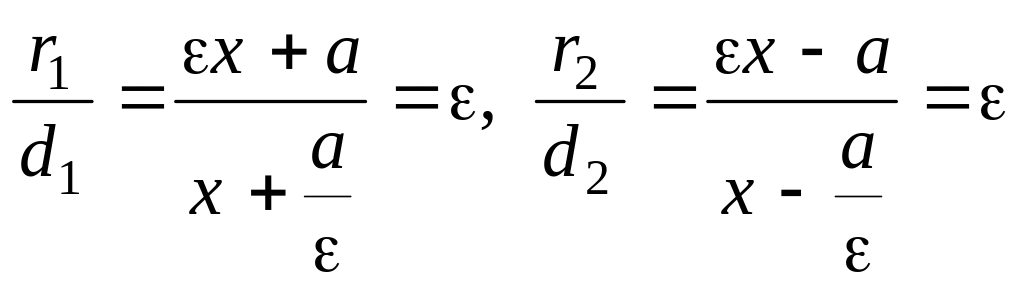Ці відношення сталі і дорівнюють ексцентриситету. Це й доводить, що прямі є директрисами.

Д ано рівняння директрис гіперболи , відстані між фокусами якої дорівнюють 10. Записати канонічне рівняння гіперболи.

 З рівностей знаходимо , а далі записуємо рівняння . 

3.4.6. Криві другого порядку

Означення. Кривою другого порядку називається геометричне місце точок площини, координати яких задовольняють рівняння

(1)

де хоча б один із коефіцієнтів відмінний від нуля.

Розглянемо квадратичну форму

а далі знайдемо власні числа матриці

з рівняння

. (2)

Позначимо корені рівняння (2) ,  і ортогональною заміною змінних

де вектори — власні вектори матриці А, перетворимо рівняння (1) до такого вигляду:

. (3)

Нехай , тоді, виділяючи повний квадрат і переміщуючи початок координат, дістанемо рівняння кривої

(4)

1. Якщо , то .

Припустимо, що . При , при , а при .

Точку можна розглядати як граничний випадок еліпса.

2. Якщо , то . Тоді при , а при .

3. Якщо в рівнянні (3) , тобто , то, узявши, наприклад,  = 0, прийдемо до рівняння

. (5)

При виділенням повного квадрата можна звести рівняння (5) до вигляду

Отже, дістали параболу. .

.

Доходимо висновку, що крива другого порядку являє собою або канонічний переріз (еліпс, параболу, гіперболу), або пару прямих (можливо, таких, що збігаються).

269