3.4. Конічні перерізи
3.4.1. Полярні координати
Положення довільної точки М на площині можна визначити за допомогою полярної системи координат. Візьмемо на площині деяку фіксовану точку О, яка називається полюсом.
З точки О проведемо промінь х, який називається полярною віссю. Кожній точці М на площині можна поставити у відповідність два числа: r — відстань точки М до полюса О і — кут між полярною віссю х і вектором ОМ (рис. 3.32).
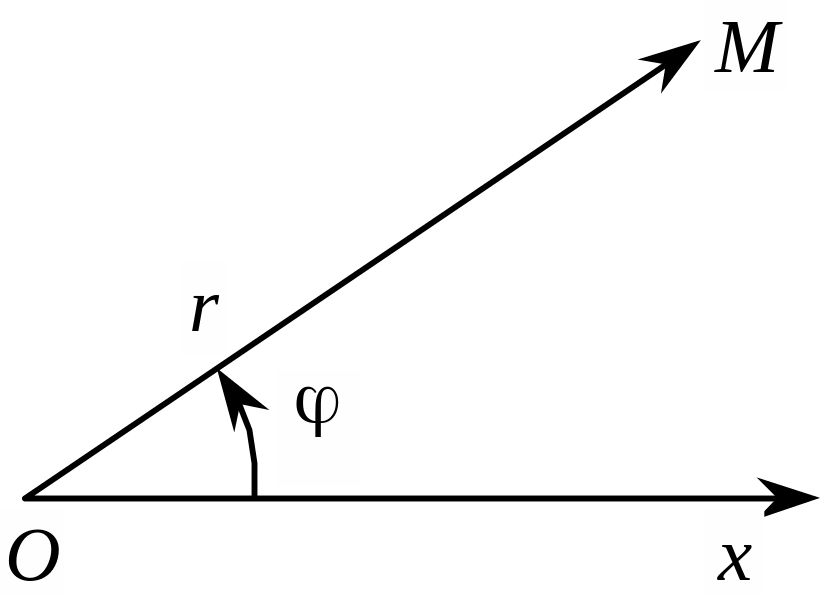
Рис. 3.32
Числа
r
і
називаються полярними
координатами
точки М.
При цьому
,
а кут
достатньо брати у проміжку [0, 2].
Означення.
Рівняння
називається рівнянням
кривої в полярних координатах,
якщо полярні координати точок, які
лежать на кривій, і тільки вони
задовольняють це рівняння.
С
кладемо
рівняння кола з центром у полюсі і з
радіусом рівняння R.
Одержимо рівняння r
= R.
С кладемо рівняння кола радіусом R, що проходить через полюс і має центр на полярній осі (рис. 3.33).
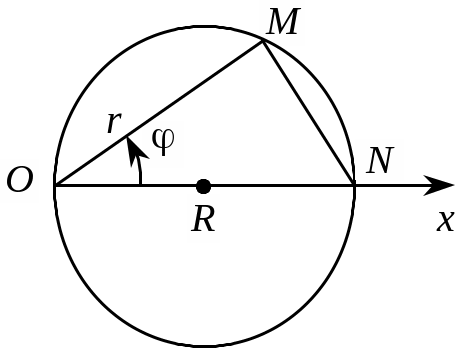
Рис. 3.33
З прямокутного трикутника ONM знаходимо, що
Розглянемо на площині прямокутну систему координат ху з початком у полюсі О (рис. 3.34).
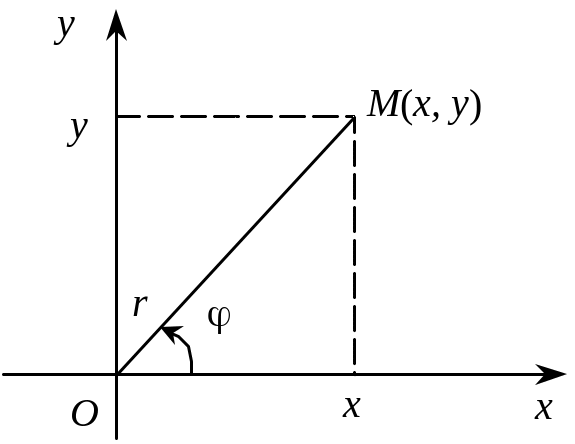
Рис. 3.34
Між декартовими координатами точки М і полярними її координатами існують такі співвідношення:
(1)
На підставі цих залежностей можна скласти рівняння кривої в полярних координатах, якщо відомо рівняння в декартових координатах, і навпаки.
Р івняння кривої, що називається лемніскатою Бернуллі, має в декартових координатах такий вигляд:
Узявши
,
дістанемо рівняння
Графік лемніскати зображено на рис. 3.35.
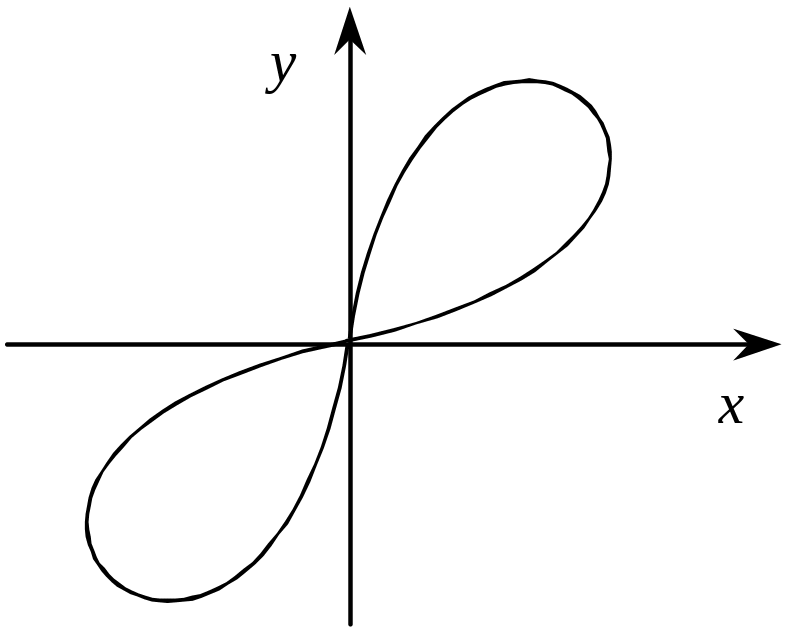
Рис. 3.35
Зауважимо, що деякі криві зручніше подавати рівняннями в полярних координатах.
С
піраллю
Архімеда називається крива, що визначається
рівнянням
(рис. 3.36).
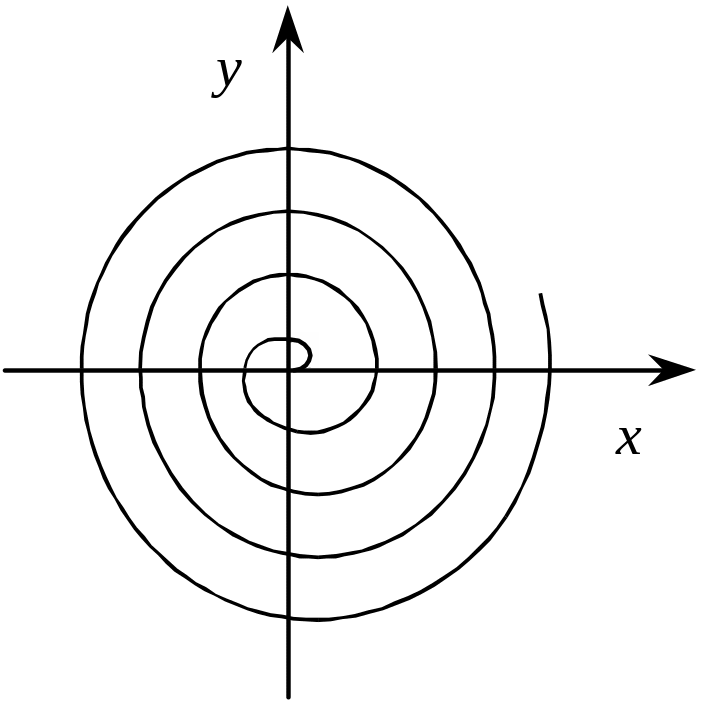
Рис. 3.35
Вигляд спіралі Архімеда має пружина в годиннику, доріжка на грамофонній платівці і т. ін.
Логарифмічною спіраллю називається крива виду
Ця крива характеризується тим, що кут між нею та її радіусом-вектором є сталим (рис. 3.37).
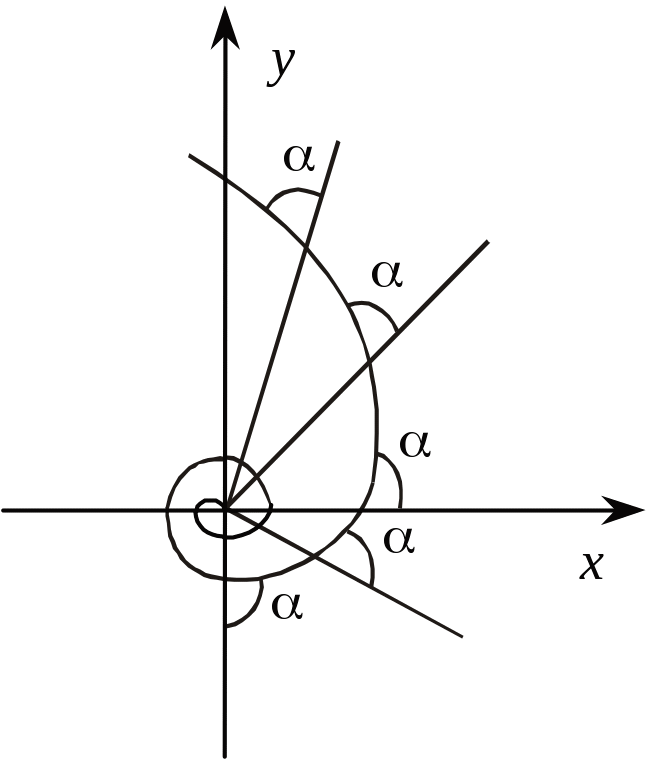
Рис. 3.37
3.4.2. Конічні перерізи
Означення. Конічним перерізом називається крива, по якій круговий конус перетинається довільною площиною, що не проходить через його вершину (рис. 3.38).
Рис. 3.38
Коли зазначена площина перетинає всі твірні конуса, у перерізі утворюється крива , яка називається еліпсом.
Крива , яка утворюється в тому разі, коли площина перерізу паралельна єдиній твірній конуса, називається параболою.
Якщо площина перерізу паралельна двом твірним конуса, відповідна крива називається гіперболою. При цьому площина перетинає обидві порожнини конуса, тому гіпербола розпадається на дві вітки.
Усі конічні перерізи мають спільні властивості, які полягають ось у чому.
Означення. Кожний конічний переріз, крім кола, являє собою геометричне місце точок площини, відношення відстаней яких від деякої фіксованої точки F, що називається фокусом, і деякої прямої, що називається директрисою, є величина стала. Це так званий ексцентриситет. Позначають його .
При
конічний переріз є еліпсом, при
— параболою, а при
— гіперболою.
Складемо рівняння конічного перерізу в полярних координатах, беручи за фокус полюс. Полярну вісь проведемо перпендикулярно до директриси (рис. 3.39).
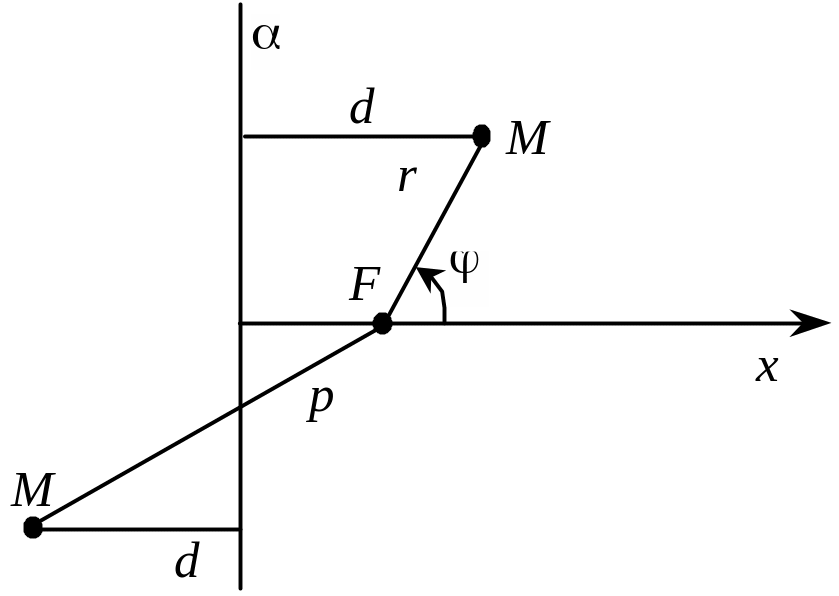
Рис. 3.39
Відстань
від фокуса до директриси позначимо р.
Відстань d
до директриси дорівнює
або
залежно від того, праворуч чи ліворуч
від директриси міститься точка. Тепер
записуємо рівняння конічного перерізу
або
(2)
Звідси маємо:
Для еліпса і параболи у формулі (2) береться знак «+», для гіперболи — обидва знаки. На рис. 3.40 зображено конічні перерізи при різних значеннях .
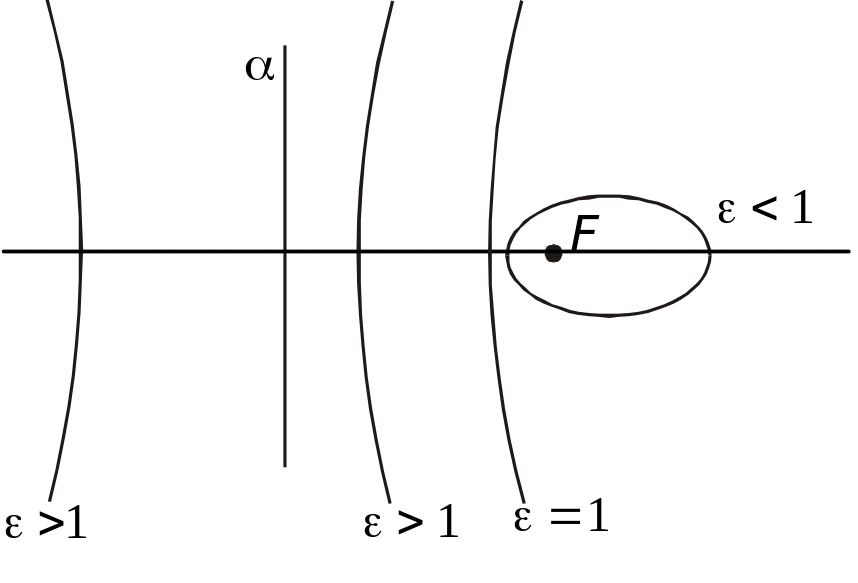
Рис. 3.40
Запишемо рівняння конічних перерізів у декартових координатах. Згідно з (2) маємо:
Узявши до уваги (1), дістанемо:
,
або
(3)
Спростимо запис рівняння при різних значеннях .
1. При = 1:
Позначивши
прийдемо до канонічного рівняння параболи
(4)
2. При виділимо в рівнянні (3) повний квадрат. Тоді дістанемо рівняння
Узявши нові координати
дістанемо рівняння
або
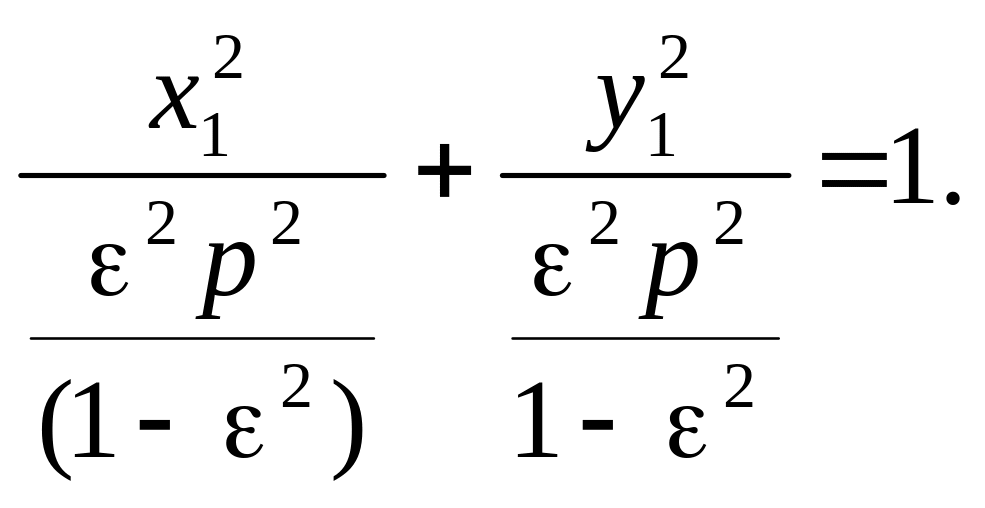
Для скорочення запису застосуємо позначення:
(5)
Остаточно маємо канонічне рівняння еліпса
(6)
При утворюється канонічне рівняння гіперболи:
(7)