Якщо м1(x1, y1, z1), м2(x2, y2, z2) — дві точки у просторі, то відстань d між ними визначається так:

(10)

Означення. Рівняння називається рівнянням поверхні, якщо координати кожної її точки задовольняють це рівняння, а координати жодної точки, яка не лежить на поверхні, не задовольняють його.

Означення. Система рівнянь

яка задає координати точок деякої поверхні, називається параметричним рівнянням цієї поверхні.

З апишемо рівняння довільної кулі із центром у точці C(a, b, c) і радіусом R.

 Кожна точка М(x, y, z), що належить поверхні цієї сфери, міститься на відстані R від центра розглядуваної кулі, а отже, її координати задовольняють рівняння

(11)

Саме воно і є шуканим рівнянням кулі.

Складемо параметричне рівняння кулі, узявши

(12)

Підставивши вирази (12) у рівняння (1), дістанемо очевидну тотожність:

Означення. Поверхня, породжувана рухом прямої лінії (твірної), паралельної нерухомій прямій, називається циліндричною. Будь-яка лінія, котру твірна перетинає в кожному своєму положенні, називається напрямною.

Якщо рівняння поверхні не містить однієї з координат, наприклад z, то це означає, що для всіх значень z вигляд поверхні однаковий. Отже, ця поверхня є циліндричною з твірною, яка паралельна осі z.

З апишемо рівняння прямого кругового циліндра з віссю z і радіусом R (рис. 3.8).



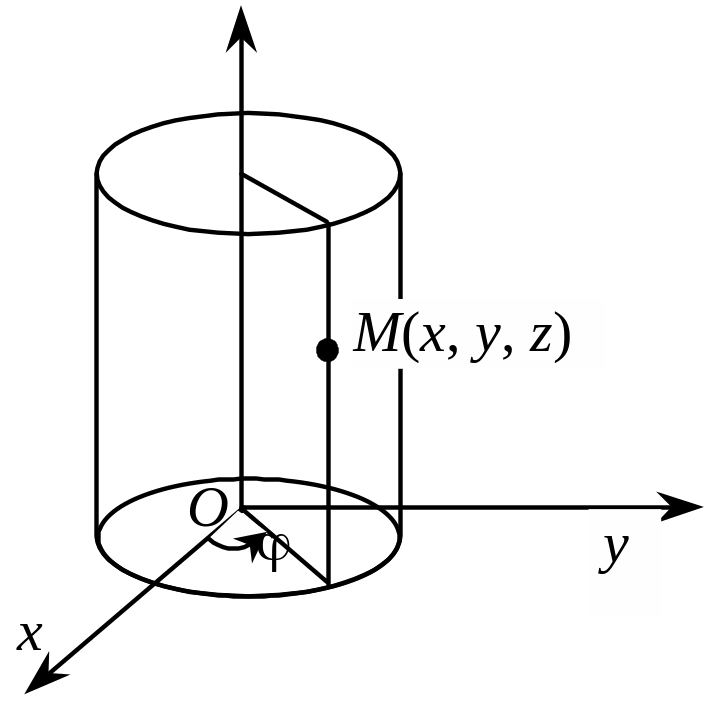
Рис. 3.8

Нехай M(x, y, z) — довільна точка на циліндрі, яка лежить на площині, що проходить через вісь z і утворює кут  з віссю х. Координата z = v.

Отже, маємо параметричне рівняння розглядуваної циліндрич­ної поверхні

Виключивши параметри  та v, дістанемо рівняння циліндрич­ної поверхні

Лінію у просторі можна розглядати як результат перетину двох поверхонь і відповідно подавати системою двох рівнянь:

Цю криву можна записати й у параметричній формі

С кладемо рівняння спіральної лінії (рис. 3.9).



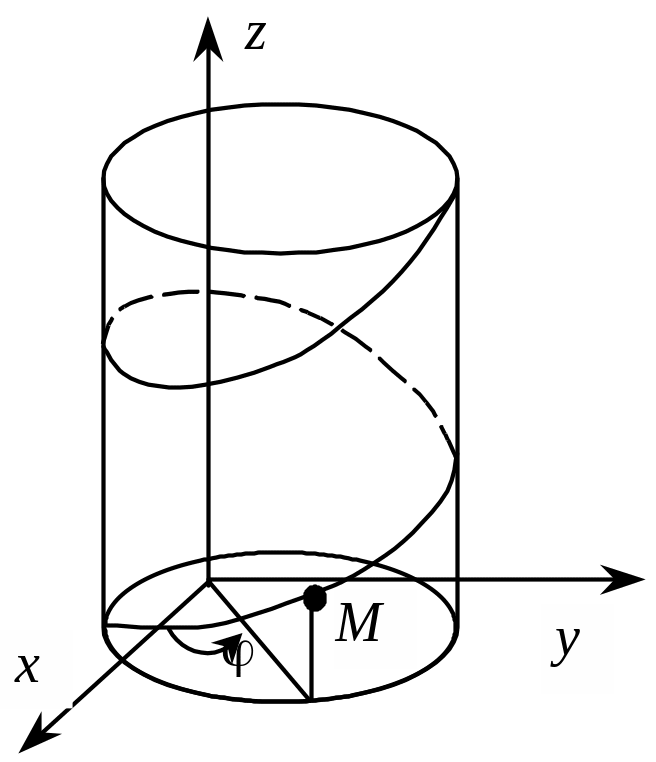
Рис. 3.9

Положення точки М можна визначити координатами:

Запишемо рівняння довільного кола у просторі. Будь-яке коло можна подати як результат перетину двох куль, тобто системою рівнянь

Точка у просторі являє собою результат перетину трьох поверхонь:

Розв’язуючи цю систему рівнянь, знаходимо координати зазначеної точки:

Рівняння останньої системи можна розглядати як рівняння поверхонь — трьох площин, які перетинаються.

3.2. Вектори

3.2.1. Додавання та віднімання векторів

Означення. Векторною величиною, або вектором (у широкому розумінні), називається будь-яка величина, що має напрям (наприклад, сила, що діє на матеріальну точку).

Означення. У геометрії вектором (у вузькому розумінні) називається напрямлений відрізок. Напрям відрізка вказується стрілкою. Розрізняють початок і кінець вектора.

Означення. Два вектори називаються рівними між собою, якщо кожний із них можна дістати паралельним перенесенням іншого.

Рівні вектори є паралельними (колінеарними), мають один і той самий напрям і однакову довжину. Довжина вектора а називається також абсолютною величиною, або модулем, вектора і позначається .

Означення. Вектор називається нульовим (нуль-вектором), якщо він має нульову довжину, тобто його кінець збігається з початком.

На письмі вектор позначається напівжирним шрифтом.

Щоб знайти суму двох векторів а і b, сумістимо початок вектора b з кінцем вектора а.

Означення. Сумою a + b векторів a та b називається вектор, початок якого збігається з початком вектора a, а кінець — із кінцем вектора b (рис. 3.10).

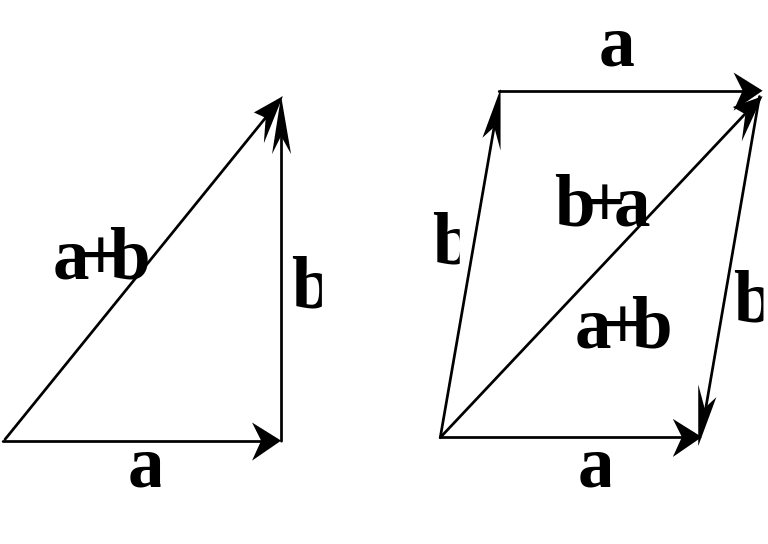
Рис. 3.10 Рис. 3.11

Додавання векторів комутативне, тобто для довільних векторів a і b справджується рівність (рис. 3.11)

a + b = b + a. (1)

Додавання векторів асоціативне, тобто для будь-яких векторів a, b, c виконується рівність

(a + b) + c = a + (b + c). (2)

Цю властивість, що випливає з означення суми векторів, унаочнює рис. 3.12.

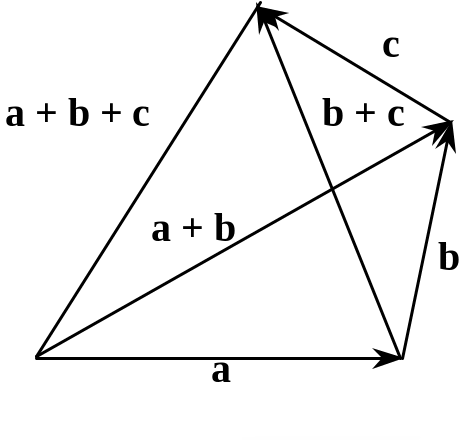
Рис. 3.12

Віднімання векторів — операція, обернена до їх додавання. Різниця b – a векторів a і b являє собою вектор, початок якого збігається з початком вектора a, а кінець — із кінцем вектора b (рис. 3.13).

a + (b – a) = b

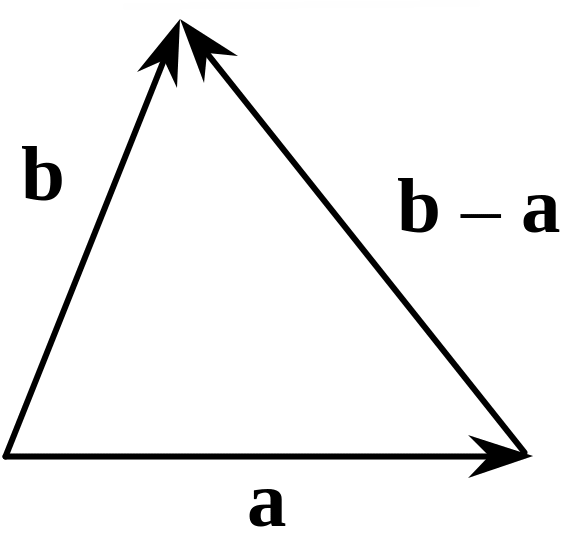
Рис. 3.13

Для будь-яких векторів a, b виконуються нерівності:

.

Розглянемо довільний вектор a і вісь х.

Означення. Якщо вектор a утворює кут  з віссю х (рис. 3.14), то проекцією вектора а на вісь називається величина

. (3)

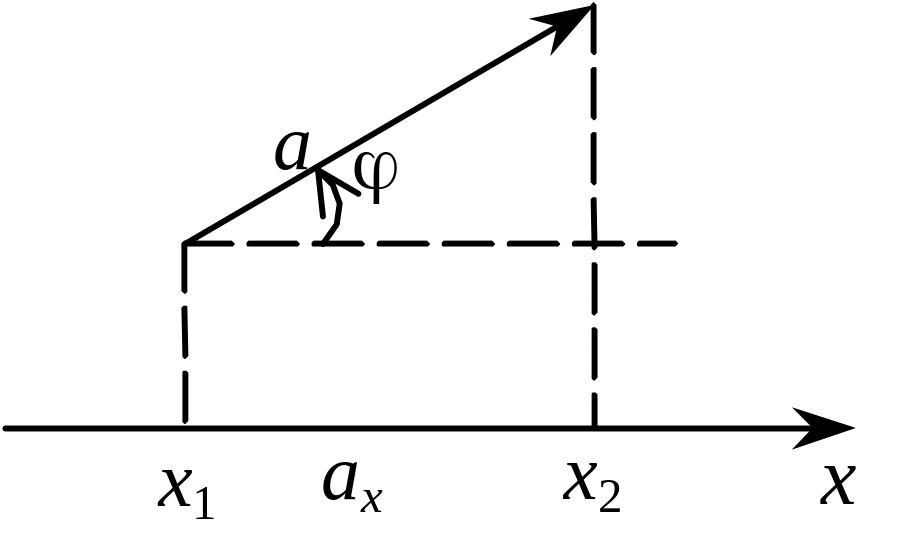
Рис. 3.14

Якщо х₁ — координата проекції початку вектора, а х₂ — координата проекції кінця вектора на вісь х, то

(4)