3.1. Метод координат
3.1.1. Декартові координати на площині
Означення. Віссю називається напрямлена пряма. Вісь називається числовою, якщо на ній вибрано початок координат і одиницю масштабу. Початок координат поділяє вісь на дві півосі — додатну і від’ємну. Координатою точки на осі називається відстань від цієї точки до початку координат, що береться зі знаком «плюс», якщо точка лежить на додатній півосі, і зі знаком «мінус», якщо вона лежить на від’ємній півосі.
Розміщення точки на осі повністю визначається її координатою.
Положення точки на площині визначається двома координатами, які відшукують так.
Проводять дві взаємно перпендикулярні прямі Ох і Оу (рис. 3.1). Їх називають осями координат. Одна з них Ох (її, здебільшого, проводять горизонтально) називається віссю абсцис, а інша — віссю ординат. Точка О їх перетину називається початком координат. Для вимірювання відрізків на осях координат вибирають деяку одиницю масштабу (довільну, але одну й ту саму для обох осей).
На кожній осі вибирають додатний напрям, який позначають стрілкою.
Додатний напрям вибирають так, щоб додатний промінь Ох після повороту на 90 проти годинникової стрілки суміщався з додатним променем Оу.
Осі координат Ох, Оу (з установленими додатними напрямами та вибраним масштабом) утворюють прямокутну систему координат*.
Розміщення точки М на площині у прямокутній системі координат визначається так. Проводимо пряму, що проходить через точку М паралельно осі Оу, і продовжуємо її до перетину з віссю Ох у точці Мх (рис. 3.1), а також пряму, що проходить через цю саму точку паралельно осі Ох до перетину з віссю Оу у точці Му. Числа х і у, які вимірюють відрізки ОМх та ОМу у вибраному масштабі (а іноді й самі ці відрізки), називаються прямокутними координатами точки М. Записують: М (х, у).
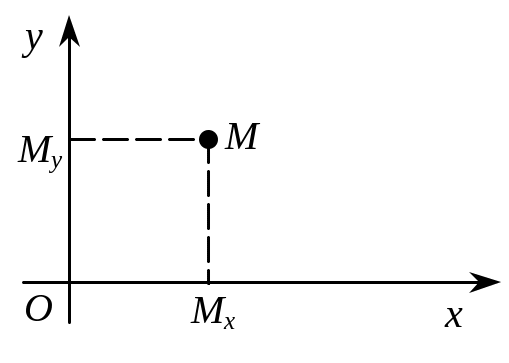
Рис. 3.1.
Число х називають абсцисою точки М, а число у — її ординатою.
Для довільної пари чисел х, у існує єдина точка М, в якої х є абсцисою, а у — ординатою.
Поряд із декартовою застосовують і інші системи координат (наприклад, полярну систему).
3.1.2. Відстань між точками. Коло
Нехай на площині ху задано дві точки М1(х1, у1), М2(х2, у2). Знайдемо відстань d між ними (рис. 3.2).
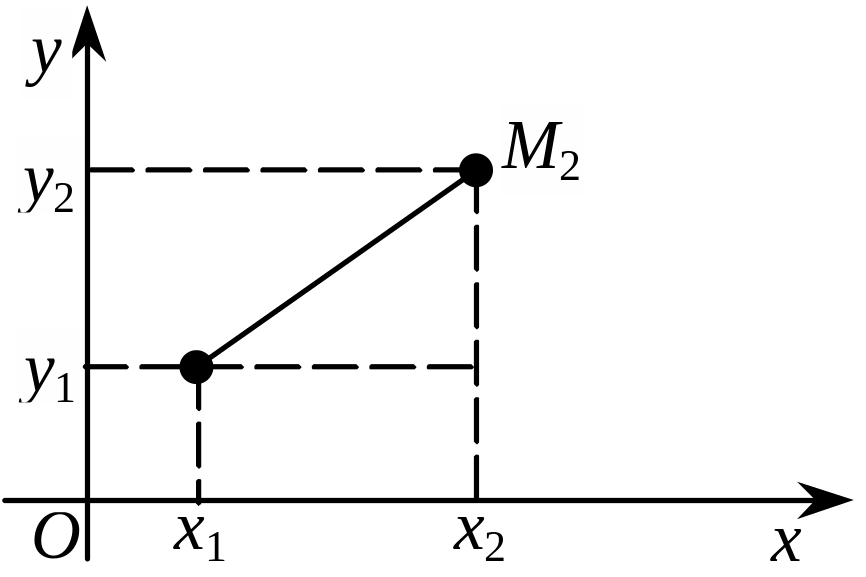
Рис. 3.2
За теоремою Піфагора маємо:
Звідси
знаходимо відстань
.
(1)
Нехай на площині ху задано деяку криву.
Означення.
Рівняння
називається рівнянням
кривої, якщо
це рівняння задовольняють координати
будь-якої точки цієї кривої і не
задовольняють координати будь-якої
точки, що не належить їй.
Запишемо рівняння кола з центром у точці C(a, b) і радіусом R. Візьмемо для цього довільну точку М(х, у) на такому колі. Оскільки відстань від точки М до центра кола С дорівнює R, то рівняння
(2)
є шуканим рівнянням кола.
У загальному випадку рівняння кола набирає вигляду
(3)
де a, b, c — деякі числа.
З найти центр і радіус кола, рівняння якого
Виділимо повний квадрат щодо х і щодо у, подавши рівняння кола в загальному вигляді:
Звідси випливає, що центр кола лежить у точці С(4, –3), а радіус кола R = 5.
Якщо точки на кривій задаються системою рівнянь
(4)
то рівняння (4) називається параметричним рівнянням кривої.
З апишемо параметричне рівняння кола з центром у точці C(a, b) і радіусом R (рис. 3.3).
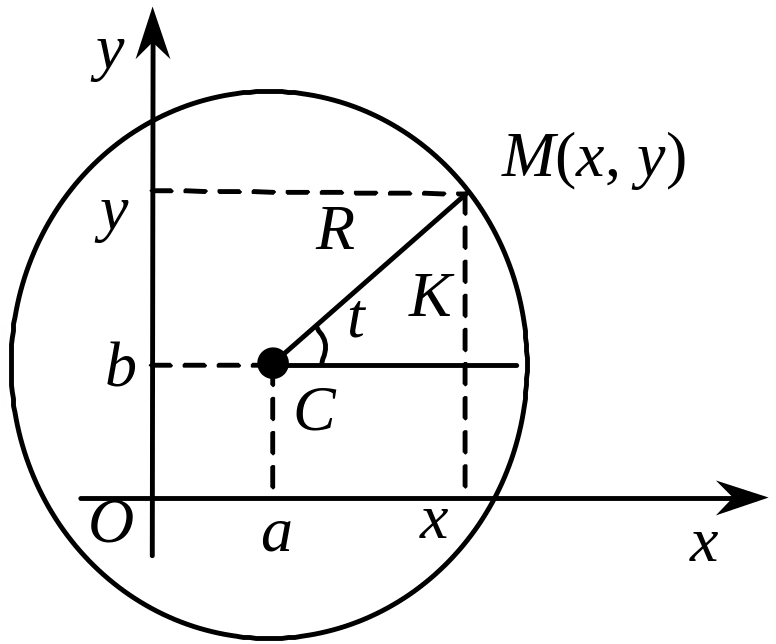
Рис. 3.3
Нехай t — кут графіка між відрізками СМ і СK. Тоді з трикутника МСK і того, що x = CK + a, y = MK + b, знаходимо параметричне рівняння кола:
(5)