
- •1.5. Нерівності, абсолютна величина
- •1.5.1. Нерівності. Системи нерівностей
- •Властивості нерівностей:
- •1.6. Відсотки
- •1.6.1. Поняття відсотка
- •1 .6.2. Три основні задачі на відсотки
- •1.6.3. Формула простого відсотка
- •Формула приросту простого відсотка:
- •1.6.4. Формула складного відсотка
- •Основна формула складного відсотка:
- •1.6.5. Економічна задача. Дисконтування
- •1.6.6. Погашення довгострокових кредитів
- •1.7. Функції
- •1.7.1. Поняття функції
- •1.7.2. Властивості функцій Означення.
- •Означення.
- •3. Функція загального виду: ні парна, ні непарна (рис. 1.30).
- •1.7.3. Функція, обернена до даної
- •1.7.4. Поняття складної (складеної) функції
- •1.7.5. Основні елементарні функції
- •Властивості
- •О сновні формули
- •Властивості
- •Основні формули
- •Основні формули
- •Основні формули
- •Властивості
- •Основні формули
- •1.7.6. Елементарні функції
- •Класифікація функцій
- •1.7.7. Деякі неелементарні функції
- •1 .7.8. Застосування функцій в економіці
О сновні формули
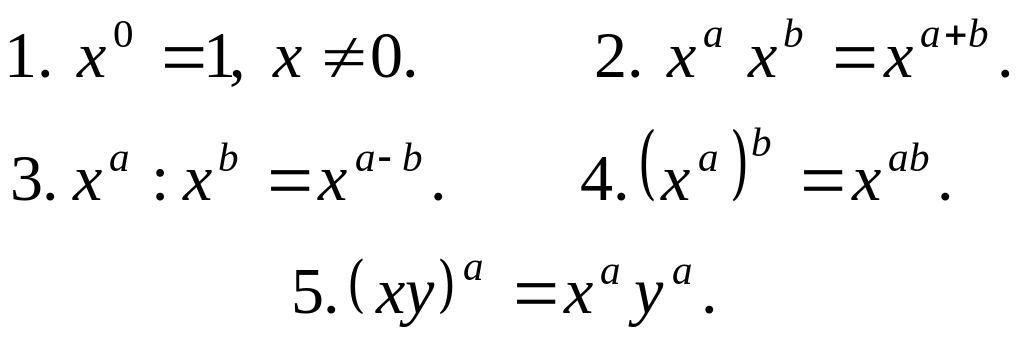
Показник степеня |
Х |
Y |
Парність |
Монотонність |
Періодичність |
Графік |
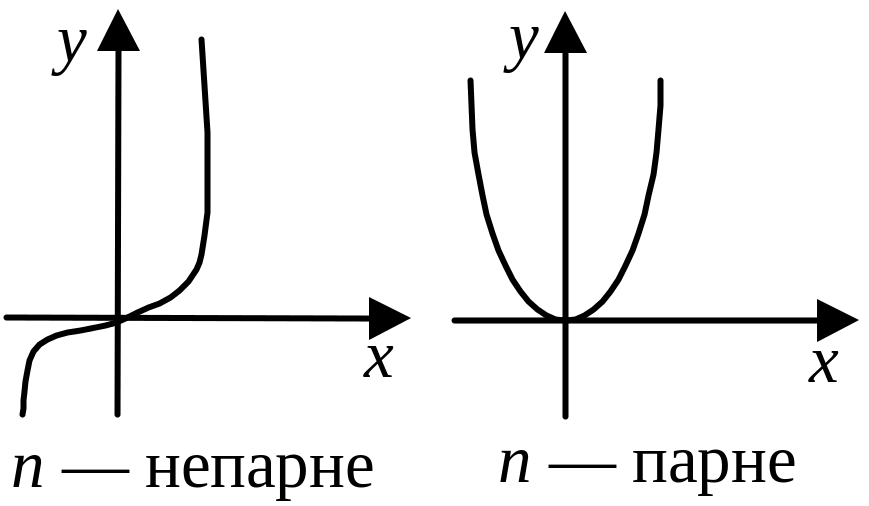
а = п, п N |
(–, +) |
(–, +), якщо п — непарне; [0; +], якщо п — парне |
Непарна, якщо п — непарне; парне, якщо п — парне |
Зростаюча на (–, +), якщо п — непарне; спадна на [–; 0] і зростаюча на [0; +], якщо п — парне |
Неперіодична |
|
|
(–, 0) (0, +) |
(–, 0) (0, +), якщо п — непарне; (0, +), якщо п — парне |
Якщо п — непарне, непарна; якщо п — парне, парна |
Якщо п — парне, зростаюча на (–, 0) і спадна на (0, +); якщо п — непарне, спадна на (–, 0) (0, +) |
Неперіодична |
|
а = 1/п, п N |
(0; +), якщо п — парне; (–, +), якщо п — непарне |
(0, +), якщо п — парне; (–, +), якщо п — непарне |
Непарна, якщо п — непарне; загального виду (ні парна, ні непарна), якщо п — парне |
Зростаюча на (–, +), якщо п — непарне; зростаюча на (0; +), якщо п — парне |
Неперіодична |
|
О значення.
Функція y = ax,
якщо a > 0,
a 1,
називається показниковою
функцією.
значення.
Функція y = ax,
якщо a > 0,
a 1,
називається показниковою
функцією.
Властивості
Х |
Y |
Парність |
Монотонність |
Періодичність |
Графік |
(– ,+ ) |
(0,+) |
Загального виду (ні парна, ні непарна) |
Якщо а > 0 — зростаюча на (– , + ); якщо a < 0 — спадна на (– , + ) |
Неперіодична |
|
Основні формули
![]()
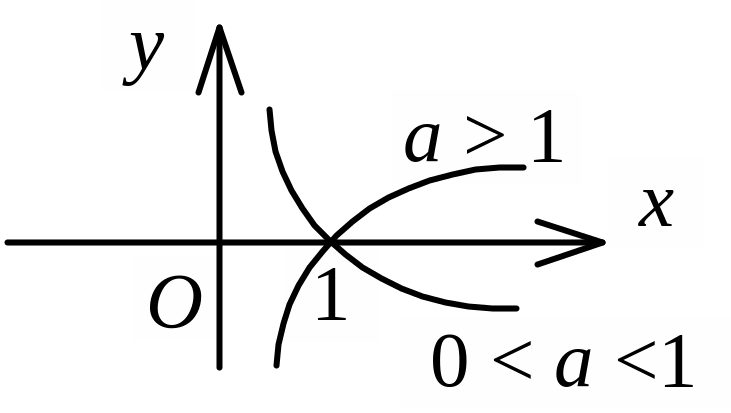
Означення. Функція y = logax, якщо a > 0, a 1, називається логарифмічною функцією. Логарифмічна та показникова функції взаємно обернені.
Х |
Y |
Парність |
Монотонність |
Періодичність |
Графік |
(0, +) |
(– ,+ ) |
Загального виду (ні парна, ні непарна) |
Якщо а > 1 — зростаюча на (0, + ); 0 < a < 1 — спадна на (0, + ) |
Неперіодична |
|
Основні формули
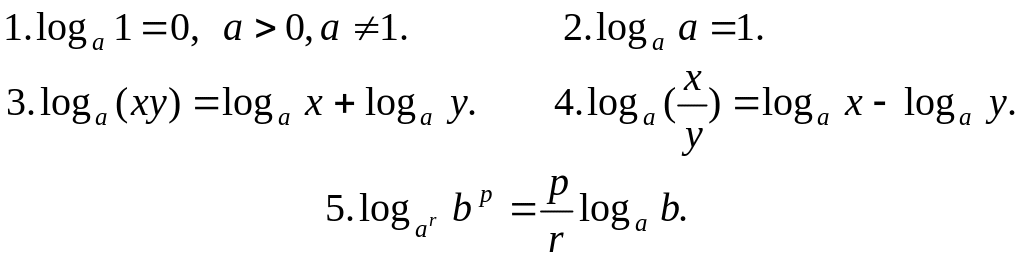
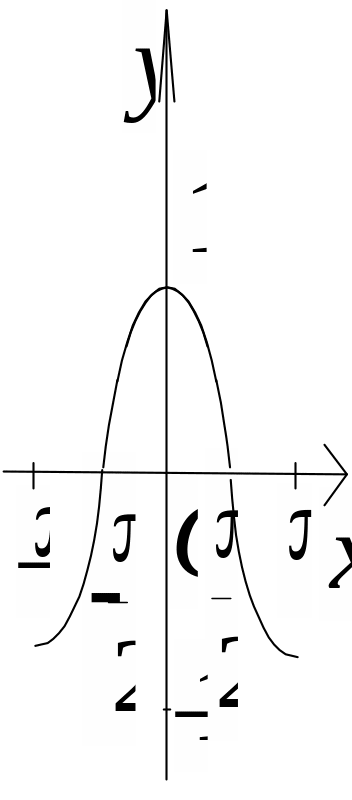
Означення. Функції y = sinx, y = cosx, y = tgx, y = ctgx називаються тригонометричними.
Властивості
Функція |
Х |
Y |
Парність |
Монотонність |
Періодичність |
Графік |
у = sin x |
(–,
+)
|
[–1; 1] |
Непарна |
Зростаюча
на
|
Періодична; Т = 2n; Тmin = 2 |
|
y = cos x |
(–, +) |
[–1; 1] |
Парна |
Зростаюча на [– + 2n; 2n]; спадна на [2n; + 2n] |
Те саме; Т = 2n; Тmin = 2 |
|
y = tg x |
|
(–, +) |
Непарна |
Зростаюча |
Те саме; Т = n; Тmin = |
|
|
(n; +n) |
(–, +) |
Непарна |
Спадна |
Те саме; Т = n; Тmin = |
|


 а
= – п,
п
N
а
= – п,
п
N
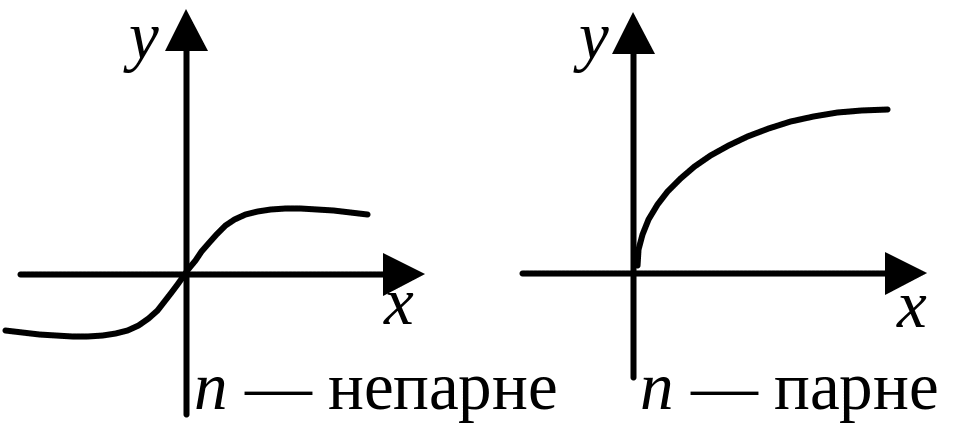
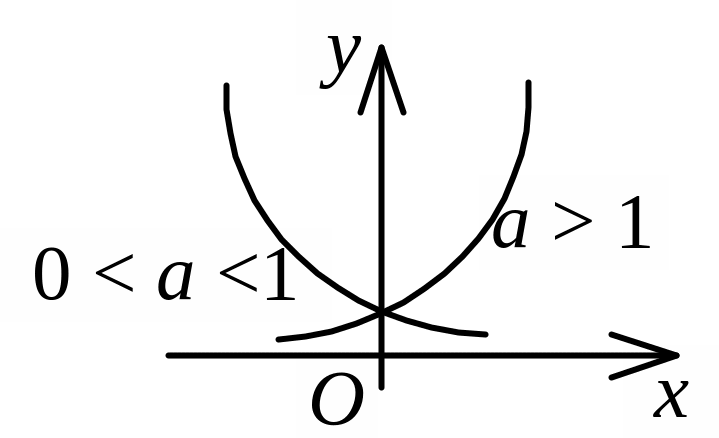

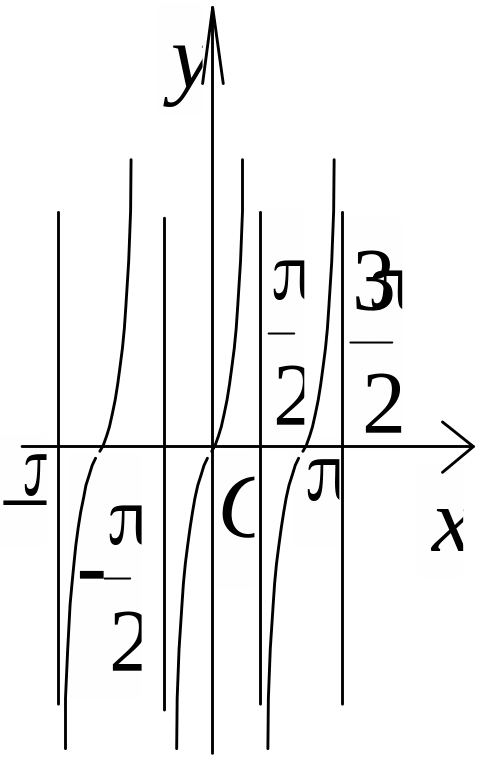
 y
=
сtg x
y
=
сtg x