
- •1.5. Нерівності, абсолютна величина
- •1.5.1. Нерівності. Системи нерівностей
- •Властивості нерівностей:
- •1.6. Відсотки
- •1.6.1. Поняття відсотка
- •1 .6.2. Три основні задачі на відсотки
- •1.6.3. Формула простого відсотка
- •Формула приросту простого відсотка:
- •1.6.4. Формула складного відсотка
- •Основна формула складного відсотка:
- •1.6.5. Економічна задача. Дисконтування
- •1.6.6. Погашення довгострокових кредитів
- •1.7. Функції
- •1.7.1. Поняття функції
- •1.7.2. Властивості функцій Означення.
- •Означення.
- •3. Функція загального виду: ні парна, ні непарна (рис. 1.30).
- •1.7.3. Функція, обернена до даної
- •1.7.4. Поняття складної (складеної) функції
- •1.7.5. Основні елементарні функції
- •Властивості
- •О сновні формули
- •Властивості
- •Основні формули
- •Основні формули
- •Основні формули
- •Властивості
- •Основні формули
- •1.7.6. Елементарні функції
- •Класифікація функцій
- •1.7.7. Деякі неелементарні функції
- •1 .7.8. Застосування функцій в економіці
1.7.2. Властивості функцій Означення.
|
монотонно зростаючою; |
строго монотонно зростаючою; |
|
монотонно спадною; |
|
строго монотонно спадною; |
|
якщо
для кожної пари
|
|
|
|
Означення.
|
парною; |
непарною; |
|
загального виду (ні парна, ні непарна) |
|
|
f(–x) = f(x); |
f(–x) = –f(x); |
|
не виконується жодна з попередніх властивостей. |
1. Парність (рис. 1.28). Осьова симетрія
|
2. Непарність (рис. 1.29). Симетрія відносно точки (наприклад, точки О)
|
3. Функція загального виду: ні парна, ні непарна (рис. 1.30).
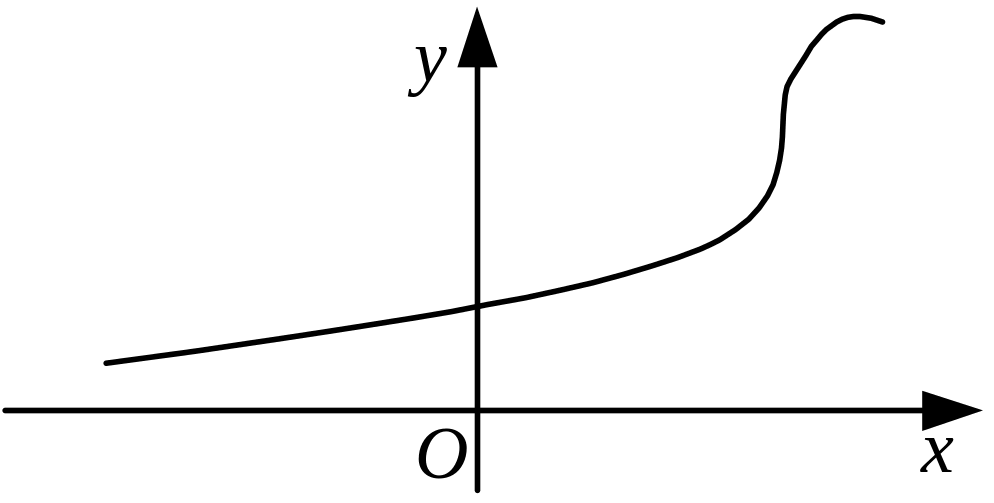
Рис. 1.30
Означення. Функція у = f(х) називається періодичною, якщо існує відмінне від нуля число Т, таке що для всіх значень х з області визначення Х виконується рівність:
![]()
Число Т називається періодом функції.
І люстрація періодичності (рис. 1.31).
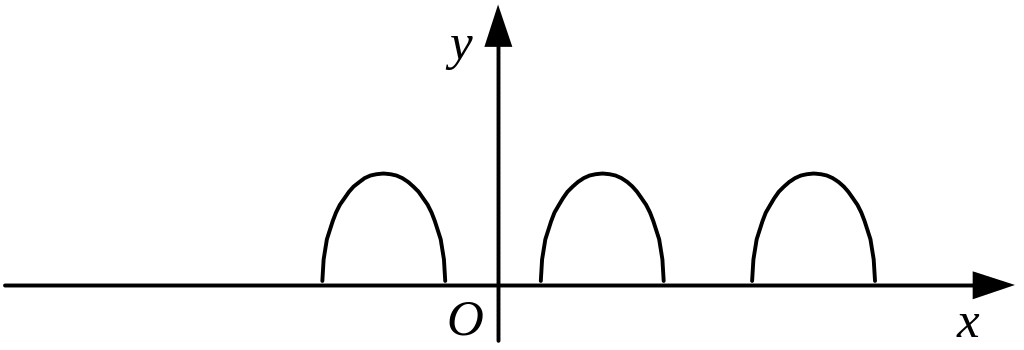
Рис. 1.31
1.7.3. Функція, обернена до даної
Розглянемо взаємно однозначну функцію у = f(х). Це означає, що кожному у із множини Y також відповідає одне і тільки одне значення х із Х (рис. 1.32).
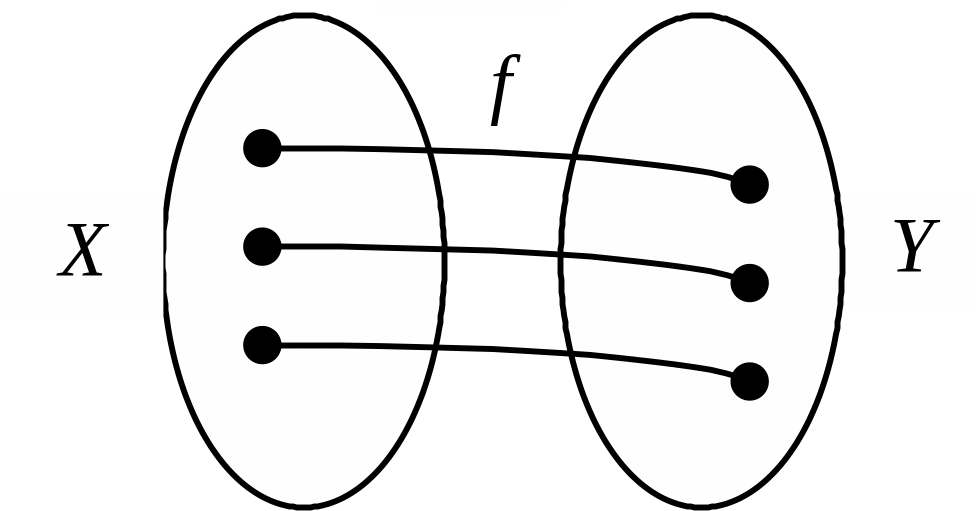
Рис. 1.32
Означення. Функцією, оберненою до функції у = f(x) (x X, y Y), називається відповідність між множинами Y та X, при якій кожному елементу з Y відповідає єдине значення з Х.
Позначення.
![]()
Якщо
в рівності
![]() у
замінити на х,
а х
виразити через у,
дістанемо функцію
у
замінити на х,
а х
виразити через у,
дістанемо функцію
![]() Цю
функцію можна також називати оберненою
до утвореної. Функції
Цю
функцію можна також називати оберненою
до утвореної. Функції
![]() та
та
![]() називаються взаємно
оберненими.
називаються взаємно
оберненими.
Геометрична інтерпретація.
Графіки двох взаємно обернених функцій симетричні відносно бісектриси квадрантів І і ІІІ (рис. 1.33):
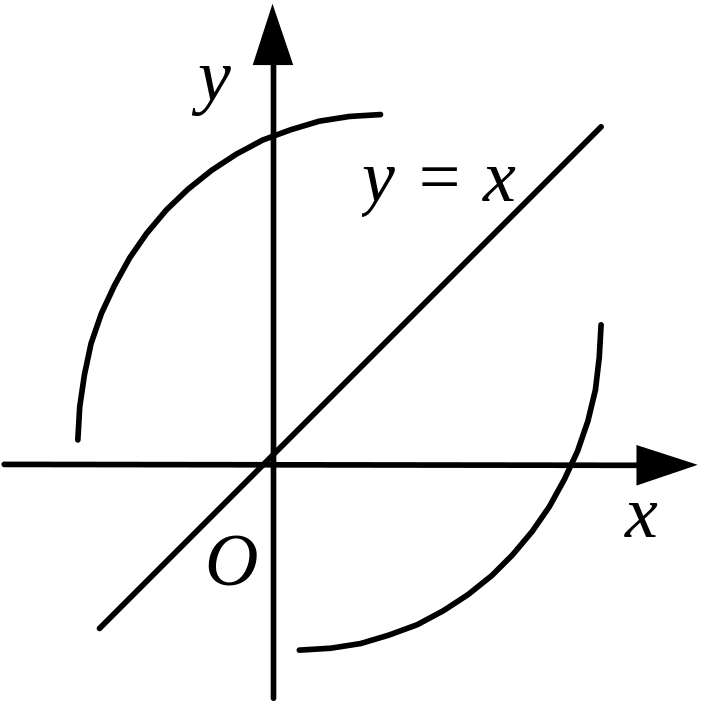
Рис. 1.33
З найдемо функцію, обернену до y = –2x + 4 (рис. 1.34).
Замінимо y на x, а х на у:
x = –2y + 4. Звідси маємо: –2y = x – 4, або y = –0,5x + 2. |
Рис. 1.34 |
1.7.4. Поняття складної (складеної) функції
Нехай маємо:
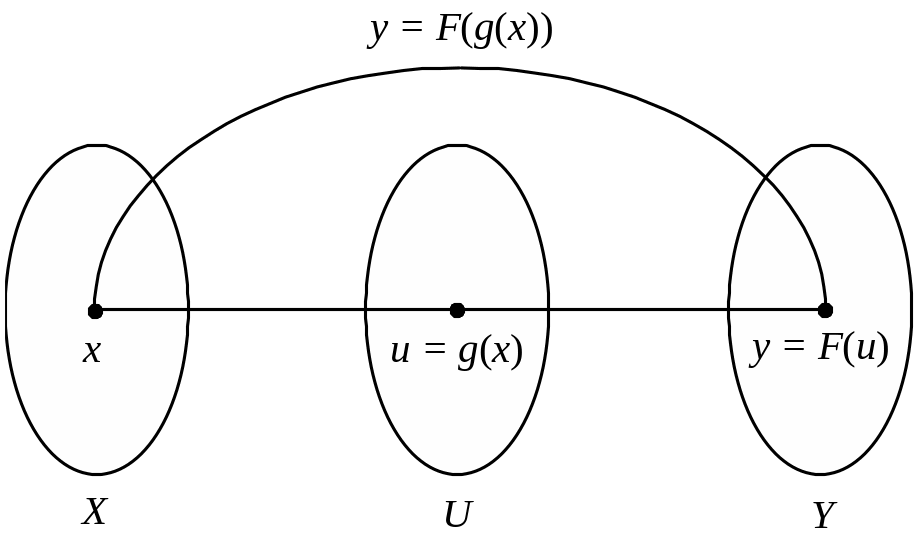
Рис. 1.35
Означення. Функція y = F(u), де u = g(x) є, у свою чергу, деякою функцією, називається складною (складеною) функцією, або суперпозицією (композицією) двох функцій.
Позначення.
![]()
1) ![]() — це композиція двох функцій: y = F(u)
= u3
i
u
= sin x;
— це композиція двох функцій: y = F(u)
= u3
i
u
= sin x;
2) ![]() — це композиція двох функцій: y = F(u)
= sin u
i
u
= x3.
— це композиція двох функцій: y = F(u)
= sin u
i
u
= x3.
1.7.5. Основні елементарні функції
Означення. Лінійною називається функція виду y = ax + b, де a, b R.
Властивості
Х |
Y |
Парність |
Монотонність |
Періодичність |
Графік |
(–, +) |
(–, +) |
Загального виду (ні парна, ні непарна), а 0; якщо а = 0 — парна |
а > 0 — зростаюча; а < 0 — спадна; а = 0 — стала |
Неперіодична при а 0, а = 0 — періодична з будь-яким періодом |
|
Означення.
Функція
![]() ,
де а
— будь-яка дійсна стала, називається
степеневою.
,
де а
— будь-яка дійсна стала, називається
степеневою.
Властивості степеневої функції, які залежать від показника а (наведені у таблиці на с. 47).

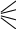 Функція
у
= f(х)
називається
Функція
у
= f(х)
називається виконується
нерівність
виконується
нерівність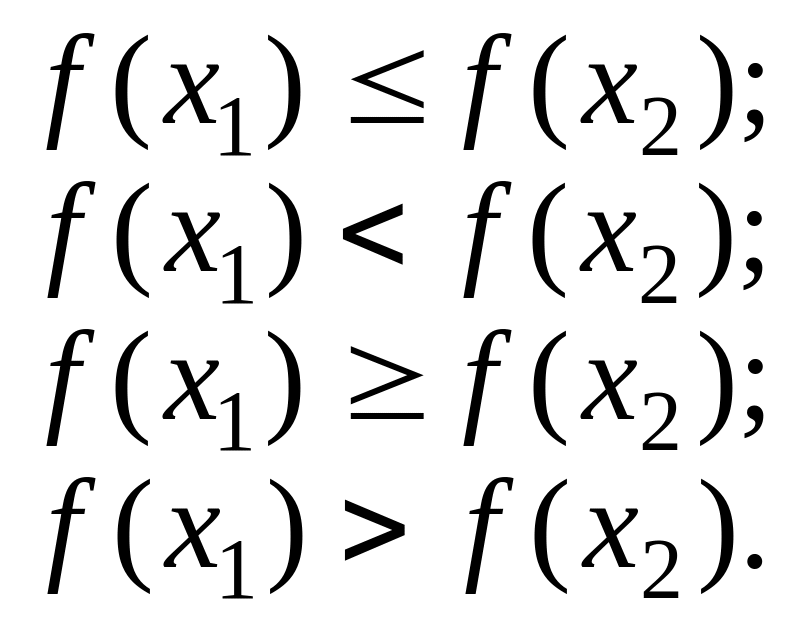
 Функція
у
= f(х)
називається
Функція
у
= f(х)
називається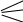 якщо
для кожного х
із Х
якщо
для кожного х
із Х
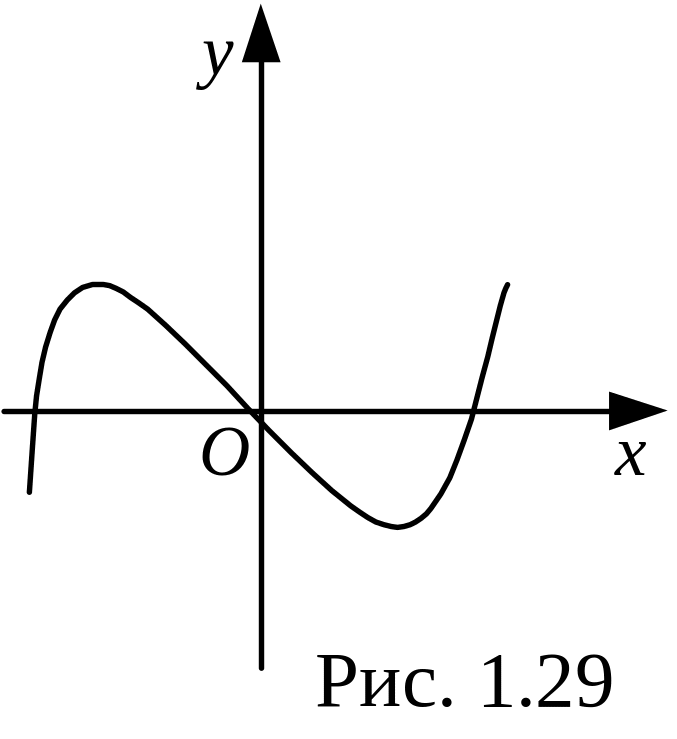
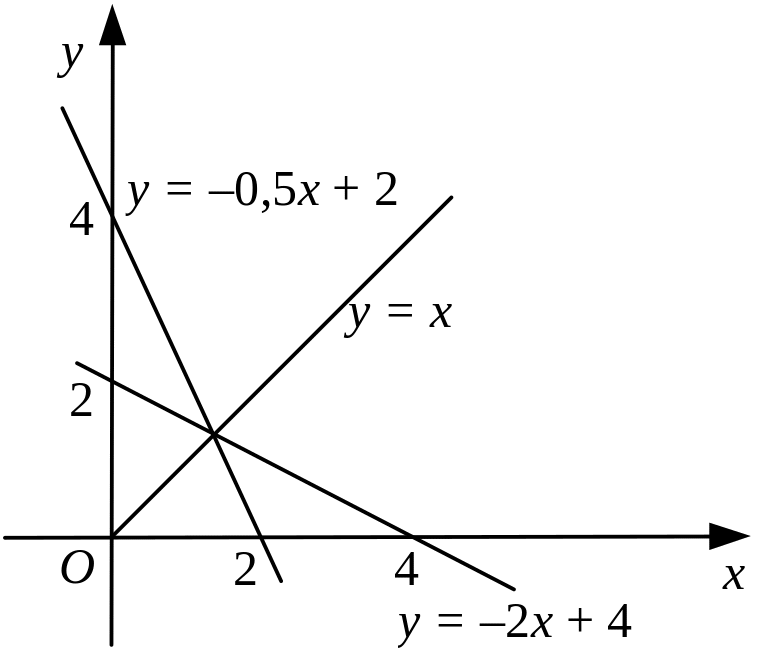
 Пряма
лінія
Пряма
лінія