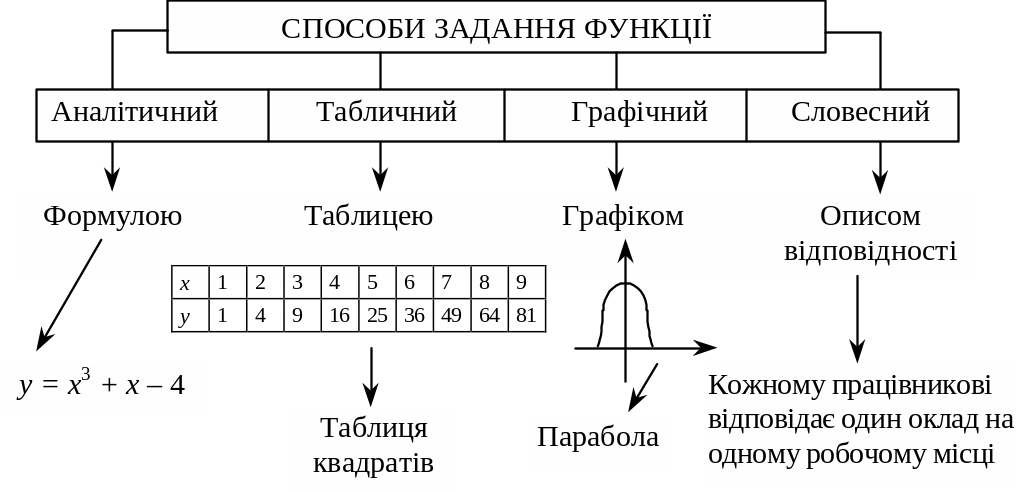
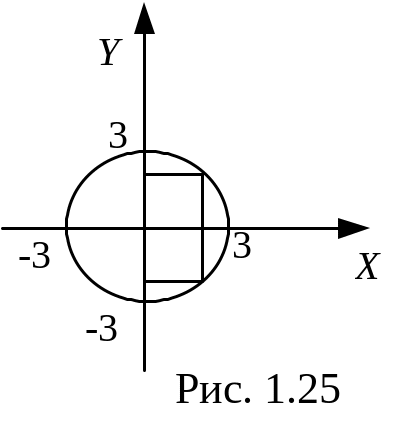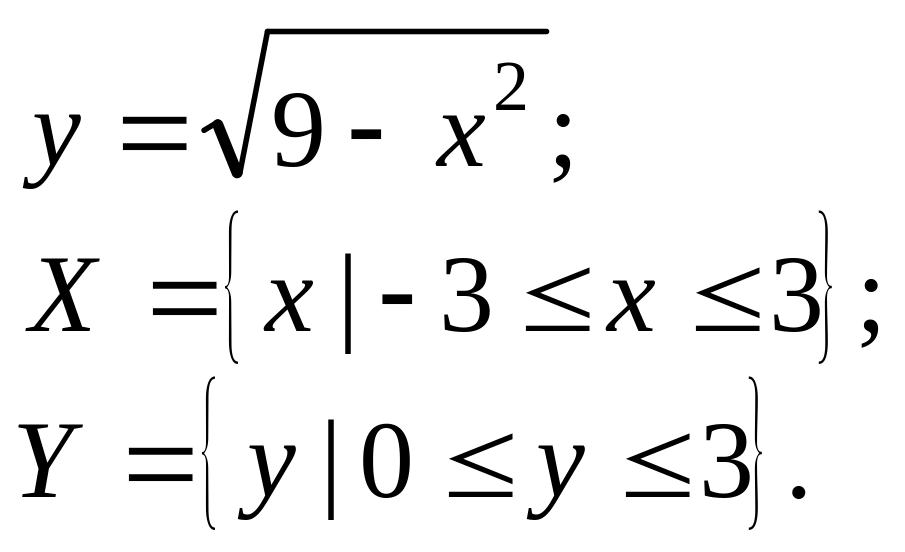- •1.5. Нерівності, абсолютна величина
- •1.5.1. Нерівності. Системи нерівностей
- •Властивості нерівностей:
- •1.6. Відсотки
- •1.6.1. Поняття відсотка
- •1 .6.2. Три основні задачі на відсотки
- •1.6.3. Формула простого відсотка
- •Формула приросту простого відсотка:
- •1.6.4. Формула складного відсотка
- •Основна формула складного відсотка:
- •1.6.5. Економічна задача. Дисконтування
- •1.6.6. Погашення довгострокових кредитів
- •1.7. Функції
- •1.7.1. Поняття функції
- •1.7.2. Властивості функцій Означення.
- •Означення.
- •3. Функція загального виду: ні парна, ні непарна (рис. 1.30).
- •1.7.3. Функція, обернена до даної
- •1.7.4. Поняття складної (складеної) функції
- •1.7.5. Основні елементарні функції
- •Властивості
- •О сновні формули
- •Властивості
- •Основні формули
- •Основні формули
- •Основні формули
- •Властивості
- •Основні формули
- •1.7.6. Елементарні функції
- •Класифікація функцій
- •1.7.7. Деякі неелементарні функції
- •1 .7.8. Застосування функцій в економіці
1.6.5. Економічна задача. Дисконтування
Означення. Обчислення початкової суми за відомим її кінцевим значенням називається дисконтуванням. Різниця D між кінцевою сумою Kn та сумою K, що дисконтується, називається дисконтом:
![]()
Якщо грошові кошти K вкладати під прості відсотки на п років за питомої відсоткової ставки і, то остаточна сума буде така:
![]()
Отже, дисконтовані грошові кошти становитимуть:
![]() .
.
У разі складних відсотків маємо:
![]()
а дисконтоване значення грошової суми
![]() .
.
Коефіцієнт
![]() називається коефіцієнтом
дисконту.
називається коефіцієнтом
дисконту.
З ауваження. На практиці для полегшення обчислень користуються таблицями, де задано значення коефіцієнтів дисконту для відповідних норм відсотка та кількості років.
Я кі грошові кошти потрібно внести до ощадної каси, щоб за умови 3% річних одержати через 10 років суму 200 000 грн.?
Коефіцієнт дисконту в десятому степені в разі 3% річних такий:
![]()
Отже, дисконтована сума становить
K = 200 000 · 0,74409=148 818 грн.
З ауваження. Якщо немає таблиць коефіцієнтів дисконту, можна скористатися таблицями логарифмів. Тоді
lgK = lg 200 000 – 10 lg 1,03.
Звідси K = 148 818 грн.
1.6.6. Погашення довгострокових кредитів
Якщо банк надає довгостроковий кредит, то має бути й план його погашення боржником за деяку кількість років, причому можливо, що боржник щороку виплачує стільки, аби погасити весь кредит, включаючи відповідні відсотки. (Як правило, внесок на погашення кредитів виплачується наприкінці кожного року.)
Нехай K — кредит, що його банк надає на n років, а R — щорічний внесок на погашення боргу наприкінці року.
Перший внесок виплачується наприкінці першого року; його дисконтована сума дорівнює Rv;
другий внесок виплачується наприкінці другого року; його дисконтована сума становить Rv2;
...........................................................................................................
n-й внесок виплачується наприкінці п-го року; його дисконтована сума дорівнює Rvп.
Кредит буде погашено, якщо початкова сума всіх виплачених внесків дорівнюватиме грошовим коштам, що надаються у кредит, тобто в разі виконання рівності:
![]()
Звідси
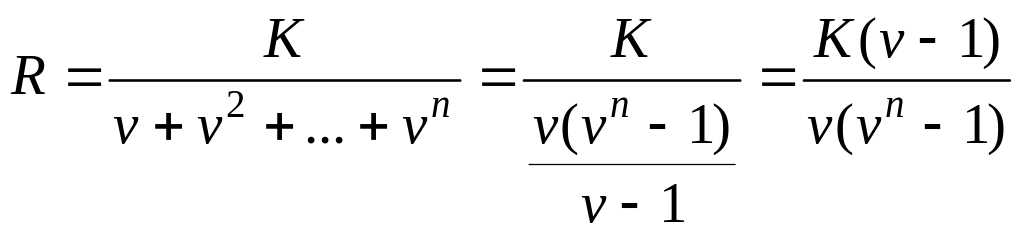 .
.
Оскільки , можна записати:
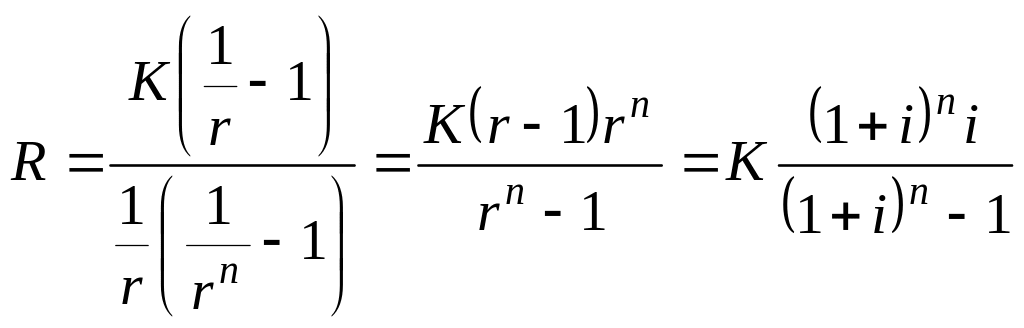 .
.
Вираз
![]() називається коефіцієнтом
погашення.
Існують таблиці значень цього коефіцієнта
для різних відсотків та строків.
називається коефіцієнтом
погашення.
Існують таблиці значень цього коефіцієнта
для різних відсотків та строків.
В ідомо, що K = 5 млн грн., і = 0,05; п = 12. Із таблиці можна знайти коефіцієнт погашення, який становить 0,11283. Тоді R = 5 000 000 · 0,11283 = 564 150 грн.
Висновок. Для того щоб погасити одержаний кредит за 12 років, боржник має виплачувати річні внески в розмірі 564 150 грн.
1.7. Функції
1.7.1. Поняття функції
Розглянемо головні види відповідності, що її можна встановити між елементами двох множин.
![]()
1. |
|
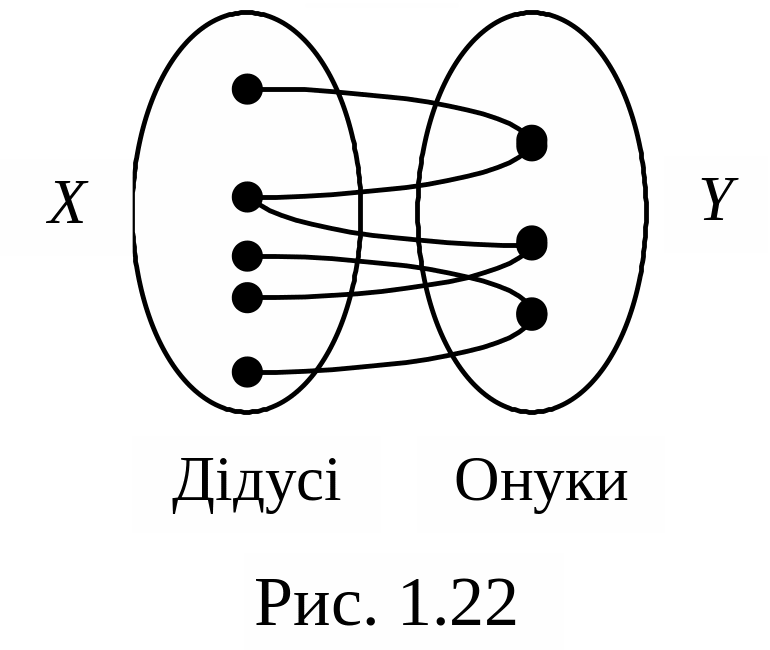
Cюр’єкція
Кожному елементу множини Х відповідає принаймні один елемент із Y (рис. 1.22). Відношення |
|
|
|
2. |
|
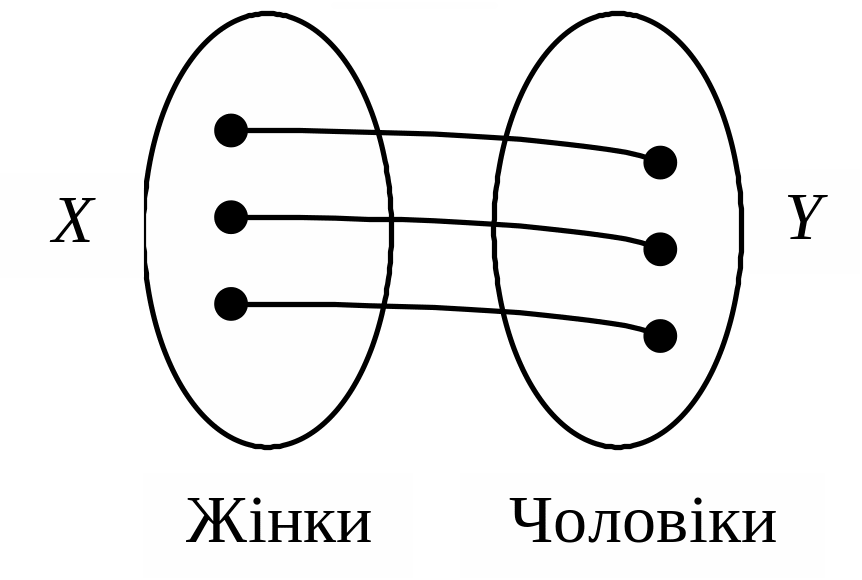
Ін’єкція
Кожному елементу з Х відповідає один елемент із Y (рис. 1.23). Функція |
3. |
(ідеальне моногамне суспільство) Рис. 1.24 |
Бієкція
Кожному елементу із Х відповідає один і лише один елемент із Y (рис. 1.24). Взаємно однозначна функція |
Розглянемо проілюстровані щойно відповідності між двома числовими множинами.
1. |
Відношення (рис. 1.25):
|
|
|
|
|
2. |
Функція (рис. 1.26):
|
|
|
|
|
3. |
Взаємно однозначна функція (рис. 1.27):
|
|
Означення. Відповідність, при якій кожному елементу х множини Х відповідає єдиний елемент y множини Y, називається функцією.
Позначення:
![]() .
.
Множина Х називається областю визначення функції, множина Y — областю значень функції. Іноді областю визначення називають множину природного існування функції, тобто множину чисел, при яких функція має сенс.
Отже, поняття функції означується за допомогою трьох понять: «область визначення», «область значень» і закономірність, згідно з якою кожному елементу з множини Х відповідає єдине значення з множини Y.