1.5. Нерівності, абсолютна величина

1.5.1. Нерівності. Системи нерівностей

Означення.

1) a < b;	b – a > 0;	а менше від b;
2) a > b;	a – b > 0;	а більше від b;
3) a  b;	b – a > 0 або b – a = 0;	а менше або дорівнює b;
4) a  b;	a – b > 0 або a – b = 0;	а більше або дорівнює b.

Геометрична інтерпретація нерівності а  b: число a міститься на числовій осі далі вліво від числа b.

( рис. 1.18).

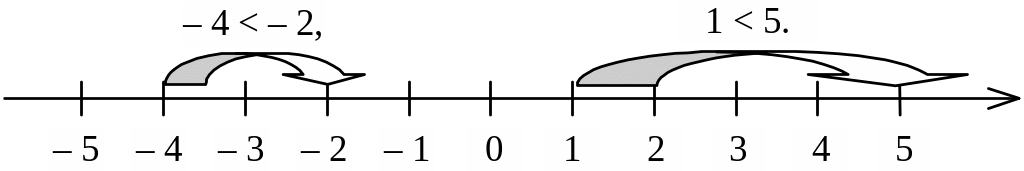
Рис. 1.18

Властивості нерівностей:

1) a  b i b  c  a  c;

2) a  b i c  d  a + c  b + d;

3) a  b  a + c  b + c; a – c  b – c;

4) a  b; c > 0  ac  bc; a/c  b/c;

a  b; c < 0  ac  bc; a/c  b/c;

– a  – b;

5)

Р озв’язати нерівність:

4 – 3х > 2x + 14.

 – 3x – 2x > 14 – 4  за властивістю 3;

– 5x > 10;

– х > 2  : 5;

x < – 2  за властивістю 4. 

Відповідь.х  х < – 2.

Р озв’язати систему нерівностей:

 З першої нерівності системи дістаємо:

.

З другої нерівності:

.

Зобразимо на площині розв’язки нерівностей (рис. 1.19).

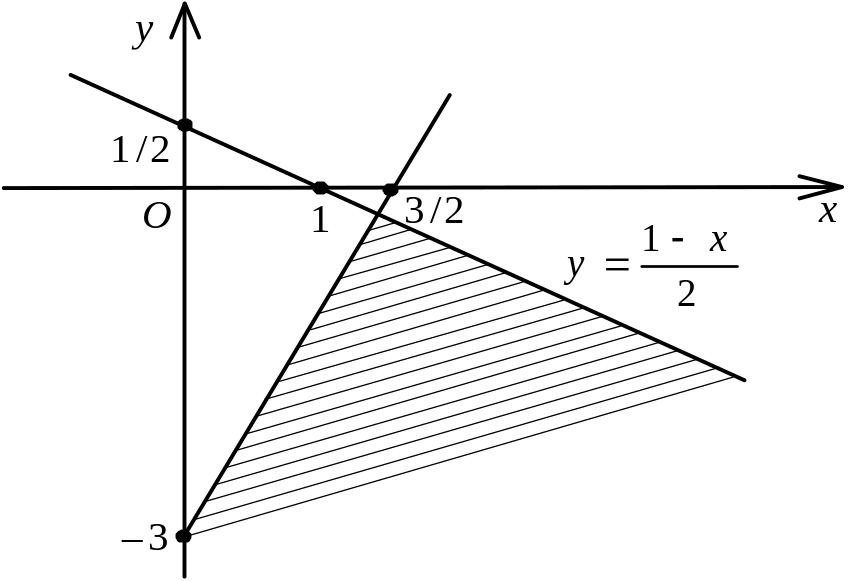
Рис. 1.19

1.5.2. Визначні нерівності

1. Нерівність Бернуллі:

.

2. Нерівність Гельдера:

3. Нерівність Коші:

.

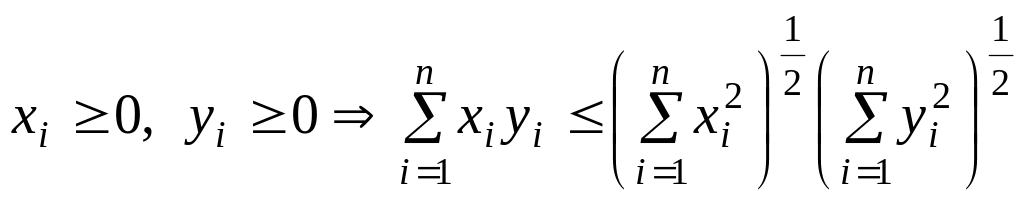4. Нерівність Юнга:

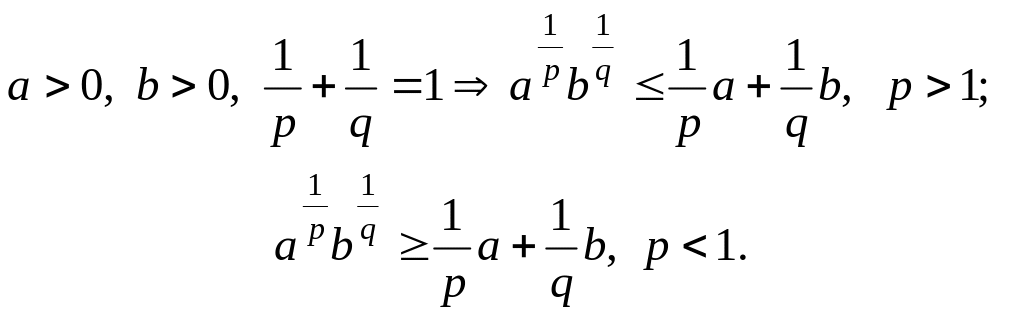
5. Нерівність Йенсена:

, f — опукла функція.

1.5.3. Абсолютна величина

Означення.

Наприклад:– 100= 100; 5 = 5.

Інтерпретація (рис. 1.20, 1.21).

Рис. 1.20

Рис. 1.21

Властивості:

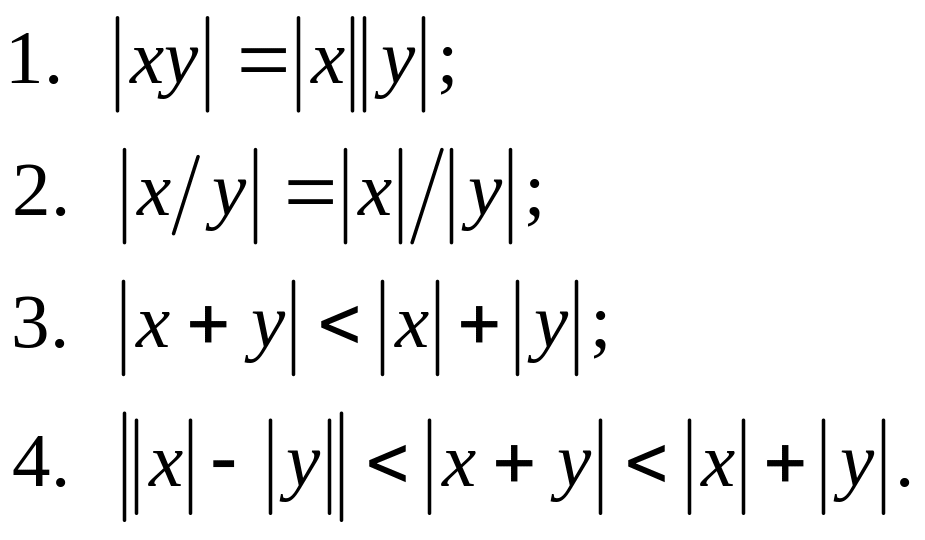
Р озв’язати нерівність:

 За означенням

– 7 < 2 – 3x < 7;

– 9 < –3x < 5;

3 > x > – 5 / 3.

Відповідь. х– 5 / 3 < x < 3}. 

1.5.4. Інтервали

Означення. Інтервалом, або проміжком, називається множина дійсних чисел, що лежать між двома даними числами a і b, задовольняючи одну із нерівностей:

a < x < b, a  x < b, a < x  b, a  x  b.

Класифікація типів інтервалів.

1) — замкнений інтервал;

2) — відкритий інтервал;

3) — напівзамкнений інтервал;

4) — нескінченні інтервали.

З ауваження. Символ +  (– ) не є числом. Це умовний знак. Він використовується для позначення змінної величини, яка може набувати значень, більших від будь-якого великого додатного числа або менших від будь-якого від’ємного числа.

1.6. Відсотки

1.6.1. Поняття відсотка

Означення. Відсотком (процентом) від числа А називається одна сота частина цього числа. Слово «відсоток» походить від латинського pro centо, що означає «із сотні». Запис 1% означає 0,01. Позначення «%» походить від перекручення запису с_to (скорочення слова cento).

Наприклад: 5% = 0,05; 5% числа А становить 0,05А.

Для того щоб знайти відсотковий вираз заданого числа (цілого чи десяткового дробу), достатньо помножити це число на 100.

В ідсотковий вираз числа 2 (відносно одиниці) є 200%; числа 0,678 є 67,8%.

Для того щоб знайти число за його відсотковим виразом, достатньо поділити відсотковий вираз на 100.

2 4,5% = 0,245; 4,5% = 0,045.