1. Загальна характеристика фізичних процесів. Детерміновані процеси та їх класифікація

Функціонування технічних та біологічних об’єктів супроводжується різноманітними фізичними явищами (процесами), які можна спостерігати. Наприклад, рух супутника по навколоземній орбіті, коливання маятника, збурення водної поверхні при зародженні та розповсюдженні хвиль, електричні сигнали на виході генератору, обертання вихідного валу двигуна.

Кожен з таких процесів можна вважати подією А, яка відбувається за певних умов S. Для визначення зв’язку між умовами, що повторюються, та подією використовується один з двох підходів:

• детермінований;

• імовірнісний.

Детермінований підхід характеризується тим, що при кожному здійсненні умов S настає подія А. Такий характер мають, наприклад, закони класичної механіки, які стверджують, що при заданих початкових умовах та силах, які діють на тіло або систему тіл, рух відбуватиметься однозначно визначеним способом.

Імовірнісний підхід полягає в тому, що при заданих умовах S подія А, в залежності від умов, що її спричинили, може відбутися, а може й не відбутися. Тобто, подія А є випадковою. Наприклад, дві характеристики електричного сигналу на виході генератору шуму за однакових умов не будуть схожими. Характерною рисою випадкових подій є те, що їх закономірності виявляються лише при багаторазовому повторенні випробувань за однакових умов.

Таким чином, будь-які отримані в процесі спостереження реальних фізичних явищ дані можна віднести до детермінованого або імовірнісного типу.

Детерміновані процеси – це процеси, які можна описати явними математичними формулами. Наприклад, тіло (масою m) підвішене за допомогою лінійної пружини (з коефіцієнтом жорсткості с) до нерухомої опори. Тіло зміщується від положення рівноваги на відстань а, потім в момент часу t=0 відпускається. На підставі багаторазових спостережень або ж за допомогою основних законів механіки можна встановити, що за відсутності згасання виконується така залежність:

, (1.1)

де .

Рівняння (1.1) дає змогу точно визначити положення тіла в будь-який наступний момент часу. Процес, що описує рух тіла, є детермінованим.

На практиці є багато явищ, які можна описати явними математичними формулами, і які за своєю суттю є детермінованими процесами. Але є багато явищ, які породжують процеси, що не можна вважати детермінованими, бо для них неможливо точно передбачити значення у наступні моменти часу (шум, вітер, висота хвиль та інші). Такі процеси є випадковими за своєю сутністю, для їх опису використовують імовірнісні та статистичні підходи. Віднесення тих чи інших фізичних явищ до детермінованого чи імовірнісного типу часто є суперечливим. З точки зору практики, рішення про детермінованість чи випадковість конкретного фізичного процесу, як правило, ґрунтується на здатності відновити процес у ході контрольного експерименту. Якщо такий експеримент призводить до одних і тих самих результатів в межах похибок), то такий процес можна вважати детермінованим. В іншому випадку – процес вважається випадковим.

Детермінований опис процесу передбачає, що є всі дані для того, щоб відтворити процес у будь-який момент часу, тобто точно передбачити часове протікання процесу х(t). Розв’язання детермінованої задачі визначається у вигляді конкретної математичної функції часу

. (1.2)

Детерміновані процеси класифікуються наступним чином:

• періодичні – гармонічні; полігармонічні;

• неперіодичні – майже періодичні; перехідні.

Найпростішими з періодичних процесів є гармонічні процеси. До таких належить синусоїдальний процес, математичний опис якого має вигляд:

, (1.3)

де х(t) – миттєве значення процесу в момент часу t; Х₀ – амплітуда; ω₀ – кругова частота, рад/с; f₀ – циклічна частота, Гц; θ – початковий фазовий кут, рад.

Інтервал часу, на протязі якого відбувається одне повне коливання, або цикл гармонічного процесу, називається періодом Т₀. Число циклів за одиницю часу називається циклічною частотою f₀. Частота і період пов’язані співвідношенням

. (1.4)

Якщо в (1.3) покласти θ=0, то отримаємо рівняння

. (1.5)

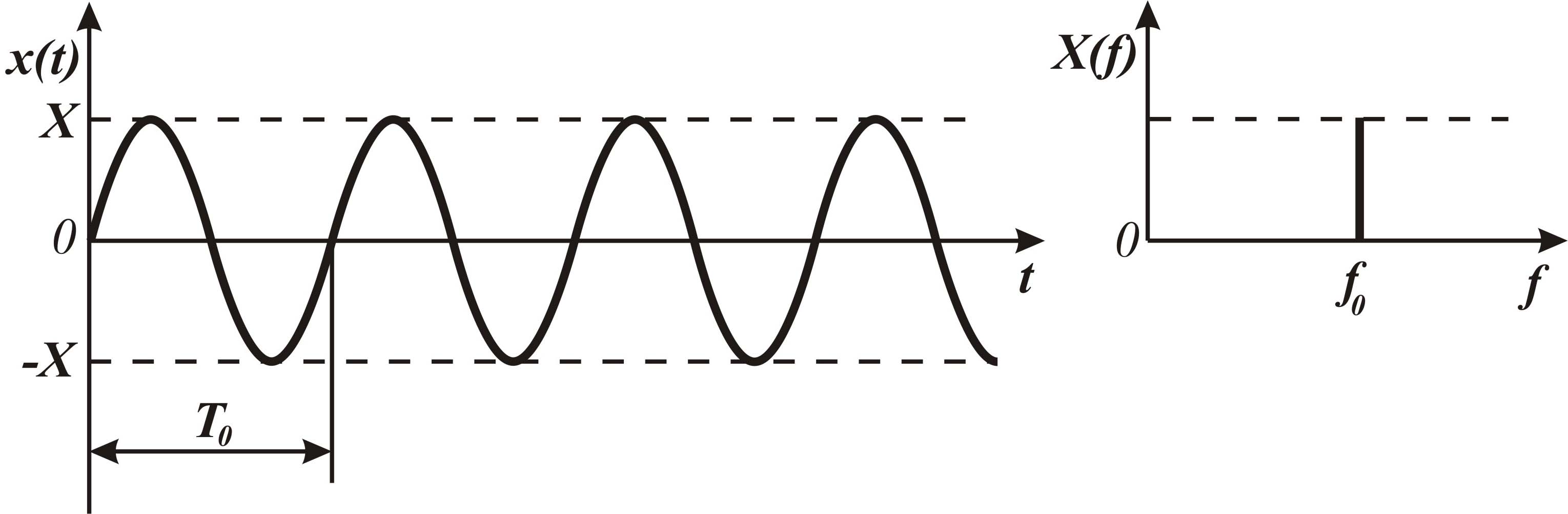
Графічно рівняння (1.5) можна зобразити у вигляді залежності миттєвого значення від часу, або у вигляді залежності амплітуди від частоти – частотного спектра, як це показано на рис. 1.1.

а) б)

Рис. 1.1. Залежність миттєвих значень від часу (а) та спектр (б) гармонічного процесу

Наведений частотний спектр складається з єдиної амплітуди (Х₀), яка розташована на певній частоті (f₀). Такі спектри називаються дискретними, або ж лінійчатими. Приклади: напруга на виході електричного генератора, процес обертання вихідного валу двигуна.

Полігармонічні процеси – це такі періодичні процеси, які математично описуються функцією часу, яка точно повторює свої значення через однакові проміжки часу

(1.6)

Проміжок часу, протягом якого відбувається одне повне коливання, називається періодом Т, а число циклів за одиницю часу називається фундаментальною частотою f₁. Гармонічні процеси – це окремий випадок полігармонічних процесів за умови f₁= f₀.

Сума двох і більше гармонічних процесів буде періодичним процесом лише тоді, коли відношення будь-яких двох частот є раціональним числом. В цьому випадку існує фундаментальний період, який задовольняє рівнянню (1.6), наприклад:

.

Якщо ж відношення частот не є раціональним числом, то фундаментальний період є нескінченно великим. Такий процес має майже періодичний характер, але (1.6) не виконується ні при будь-якому скінченому Т. Приклад функції часу, що описує майже періодичний процес:

.

Такі процеси породжуються не пов’язаними між собою джерелами гармонічних процесів, наприклад, загальна вібрація літака.

Всі інші неперіодичні процеси відносяться до перехідних, які можна задати будь-якою функцією часу, як показано на рис. 1.2.

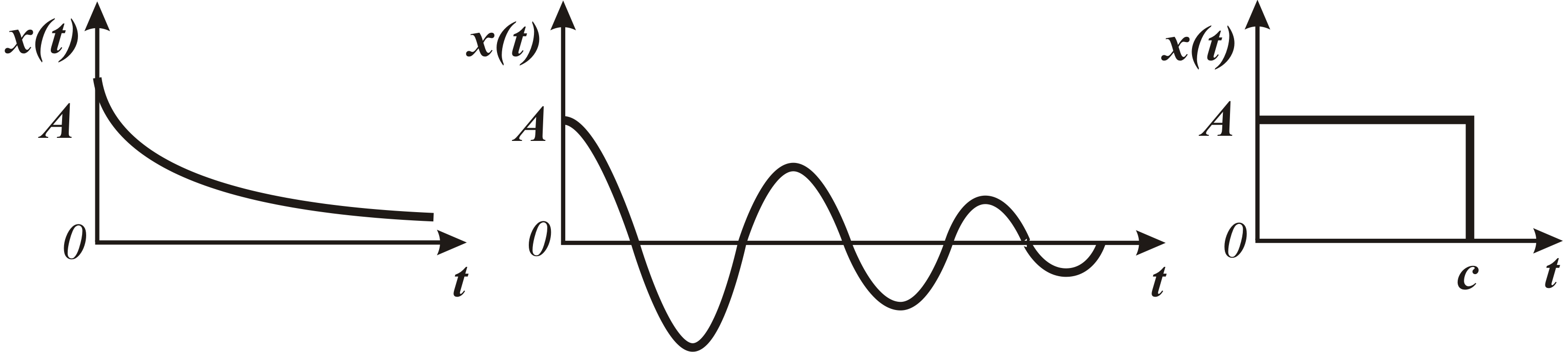
Рис. 1.2. Приклади неперіодичних процесів

2. Лабораторна робота 1

Функції генерування одиночних імпульсів

Мета роботи – вивчення функцій пакету Signal Processing Toolbox: rectpuls, tripuls, gauspuls, sinc для генерування типових одиночних імпульсів у середовищі MATLAB та одержання навичок генерування імпульсів з використанням цих функцій.

2.1 Прямокутний імпульс

2.1.1 Теоретичні відомості

Для формування імпульсу прямокутної форми служить функція rectpuls:

y=A*rectpuls (t, width),

де y – вектор значень прямокутного імпульсу центрованого відносно t=0, A – амплітуда, t – вектор значень часу, width – ширина (тривалість) імпульсу.

Результат, що повертається функцією, дозволяє утворити вектор у значень сигналу центрованого щодо t=0 за заданим вектором t моментів часу. Вектор y визначається за формулою:

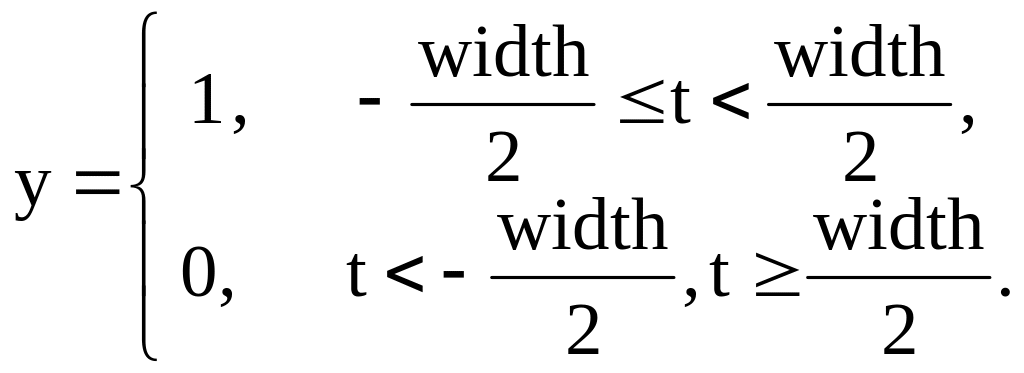(2.1)

Параметр width можна опустити, тоді його значення за замовчуванням рівне 1.