3.Решение системы нелинейных уравнений
Пример : Решить систему уравнений
(*)
Напомним, что необходимым и достаточным
условием того, что пара чисел (x,y)
является решением системы (*) тогда и
только тогда, когда она является решением
следующего уравнения с двумя неизвестными:
(**). С помощью средства Поиск решения
вместо системы (*) будем решать
равносильное ей уравнение (**). Заметим,
что геометрически решения системы (*)
описывают точки пересечения прямой с
окружностью, радиус которой равен
.
Следовательно, уравнение (**) имеет не
более двух различных решений.
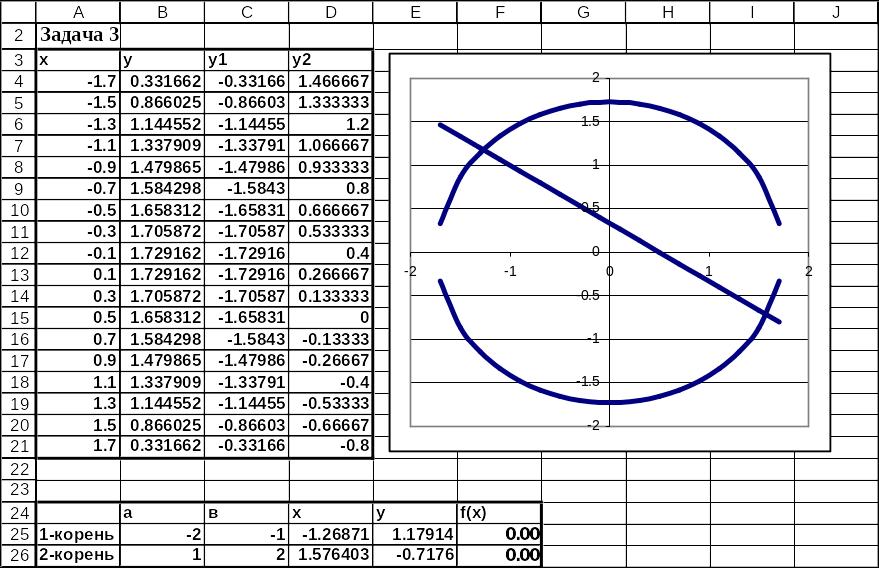
Рис.8 Отделение корней графическим способом и решение системы нелинейных уравнений
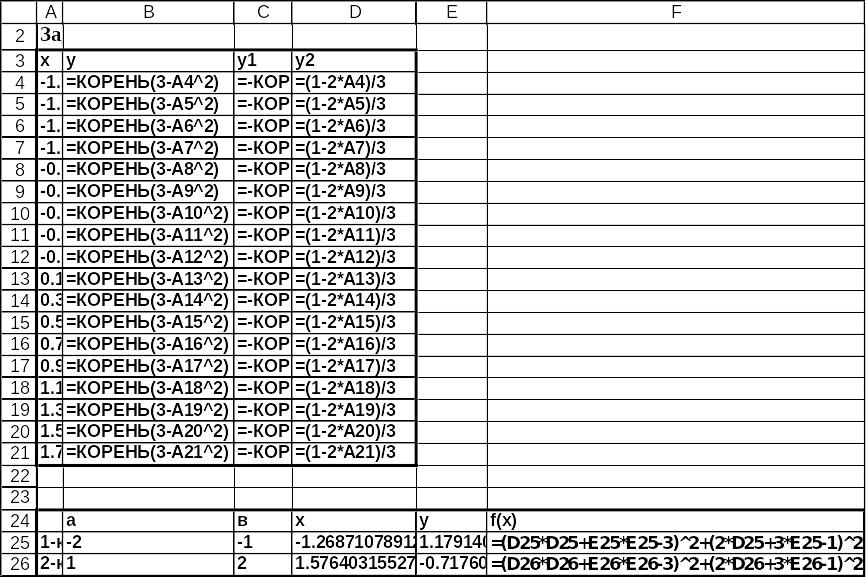
Рис.8 Решение системы нелинейных уравнений в режиме отображения формул
Вывод: первое решение
второе решение
Таблица 3
Найти решения системы нелинейных уравнений
№ |
Задание |
№ |
Задание |
|
|
9x2 – 16y2 = -144 x = 0,5 y |
|
(x + 2)2 + y2 = 9 y = 3 cos(x) |
|
|
x + y = 8 x2 + y2 = 16 + 2 xy |
|
x – y = 7 x2 + y2 = 9 – 2 xy |
|
|
x2 + y2 = 25 y = sin(x) |
|
9x2 – 16y2 = -111 x + 3y = 18 |
|
|
(x + 2)2 + y2 = 9 x – 3y = 7 |
|
x2 + y2 = 16 + 2 xy x = 3,5 y |
|
|
x2 + y2 = 9 – 2 xy y = sin(2x) |
|
x2 + y2 = 15 y = 2 cos(x) |
|
|
7x2 – 16y2 = -144 y = 3sin(x) |
|
(x + 2)2 + y2 = 9 2x - ey = 3 |
|
|
x2 + y2 = 16 + 2 xy 3x – y = 17 |
|
x2 + y2 = 9 – 2 xy y = cos(3x) |
|
|
2x2 + y2 = 25 x - ey = 3 |
|
x2 + 2y2 = 25 x + 2y = 16 |
4. Функция спроса. Равновесная цена.
Один из важнейших разделов микроэкономики – изучение спроса и предложения. Спрос на некоторый товар – это потребность в определенном количестве товара, ограниченная действующими ценами и платежеспособностью (доходами потребителей). Предложение – это количество товара, которое может быть представлено для продажи по данной цене.
Очевидно следующее утверждение: увеличение выпуска требует дополнительных затрат и, для того чтобы заинтересовать производителя в увеличении выпуска, нужно предложить ему повышенную цену. Отсюда следует, что предложение S нужно рассматривать как возрастающую функцию цены P. Если предложение зависит от цены, то и цена зависит от предложения. Экономисты обычно именно функцию P=S(Q) называют функцией предложения; а ее график – кривой предложения; где Q – количество товара предложенного для продажи по цене Р.
Так же очевидно другое утверждение: если цена на определенный товар начинает расти, то количество проданного товара будет уменьшаться, т.е зависимость спроса D от цены – убывающая функция. Экономисты называют функцией спроса функцию P=D(Q), а ее график – кривой спроса ; где Q – количество товара, приобретенного потребителями по цене Р.
Выбор функций делается на основе анализа реальной ситуации.
Некоторые содержательные выводы о взаимном влиянии показателей можно сделать, исследуя поведение соответствующих функций. Рассмотрим следующий пример.
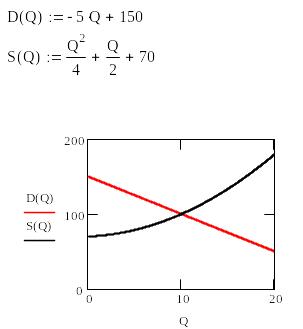
Рис.9 Нахождение равновесной цены
Представляет интерес точка кривых спроса и предложения. Эта точка называется точкой равновесия, а соответствующая цена – равновесной ценой. Пересечение графиков при P=100 спрос и предложение совпадают. При ценах ниже равновесной (P<100) спрос превышает предложение D(Q)>S(Q), возникает дефицит товара и производители могут повышать цену, рыночная цена стремится к равновесной. Если цена выше равновесной цены(P>100), то S(Q) больше D(Q) , предложение превышает спрос, остается не реализованная продукция, что побуждает производителей снижать цену, и рыночная цена будет стремиться к равновесной.
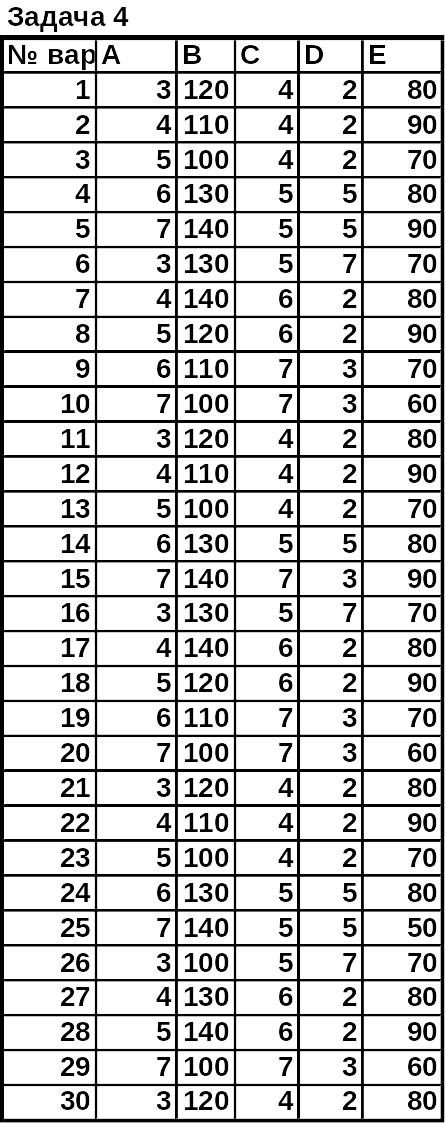
Задание к задаче 4.
Изобразите кривые спроса и предложения. Найдите равновесную цену.
Выполните для функций
D(Q)=-A*Q+B
S(Q)=Q2/C+Q/D+E.
таблица 4
