Лабораторная работа №1 Тема: Использование надстройки «Поиск решения» для решения уравнений и систем
Цель работы: Вспомнить основы численных методов для решения систем линейных и нелинейных уравнений. Освоение работы с надстройкой Excel "Поиск решения".
Каждый вариант содержит 4 задачи.
Решить систему линейных уравнений А) Методом обратной матрицы. Б) Методом Гаусса. Варианты приведены в таблице 1.
Решить нелинейное уравнение А) в надстройке «Поиск решения» Б) методом Ньютона. Варианты приведены в таблице 2.
Решить систему нелинейных уравнений в надстройке «Поиск решения». Варианты – в таблице 3.
Определить равновесную цену спроса и предложения. Номера вариантов определяются в таблице 4.
1. Решение системы линейных уравнений
Метод Гаусса
Для иллюстрации смысла метода Гаусса рассмотрим систему линейных уравнений:
Эту систему запишем в матричном виде:
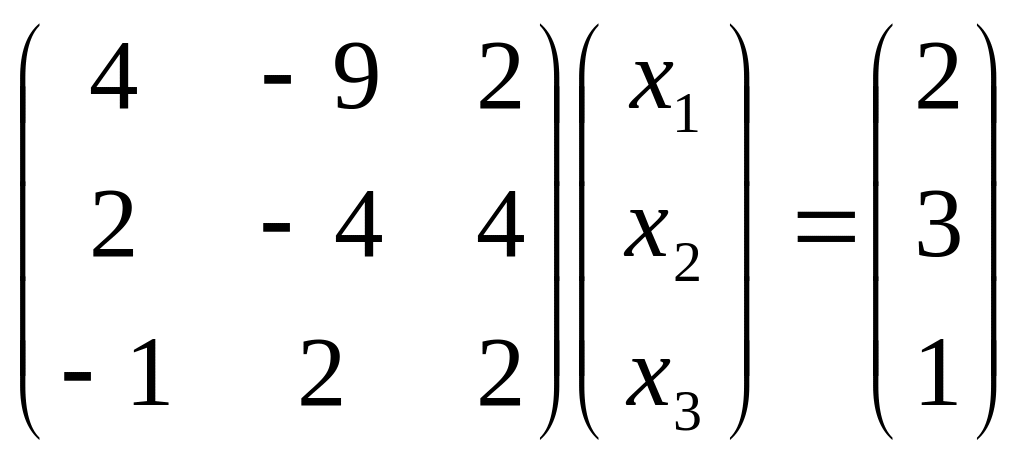
Как известно, обе части уравнения можно умножить на ненулевое число, а также можно из одного уравнения вычесть другое. Используя эти свойства, постараемся привести матрицу системы к треугольному виду, т.е. к виду, когда ниже главной диагонали все элементы – нули. Этот этап решения называется прямым ходом.
На первом шаге прямого хода умножим первое уравнение на 0.5 и вычтем из второго, тогда исключится переменная x1 из второго уравнения. Затем, умножим первое уравнение на -0,25 и вычтем из третьего, тогда система преобразуется в систему вида:
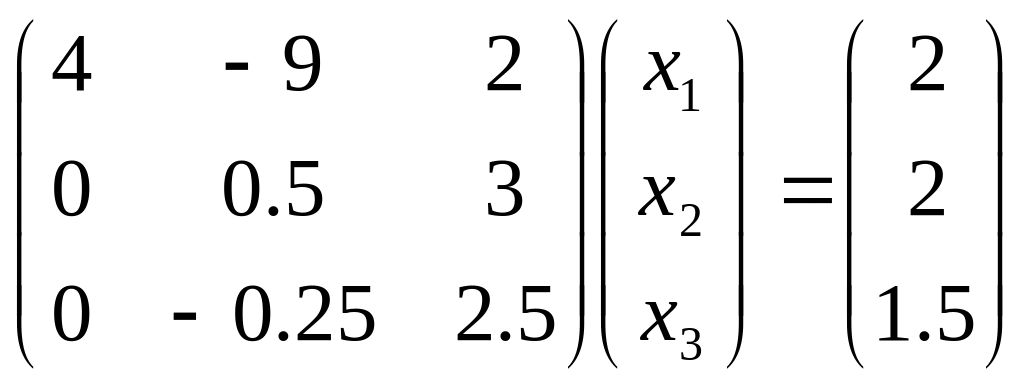
На втором шаге прямого хода из третьего уравнения исключаем x2, т.е. из третьего уравнения вычитаем второе, умноженное, на -0,5, что приводит систему к треугольному виду
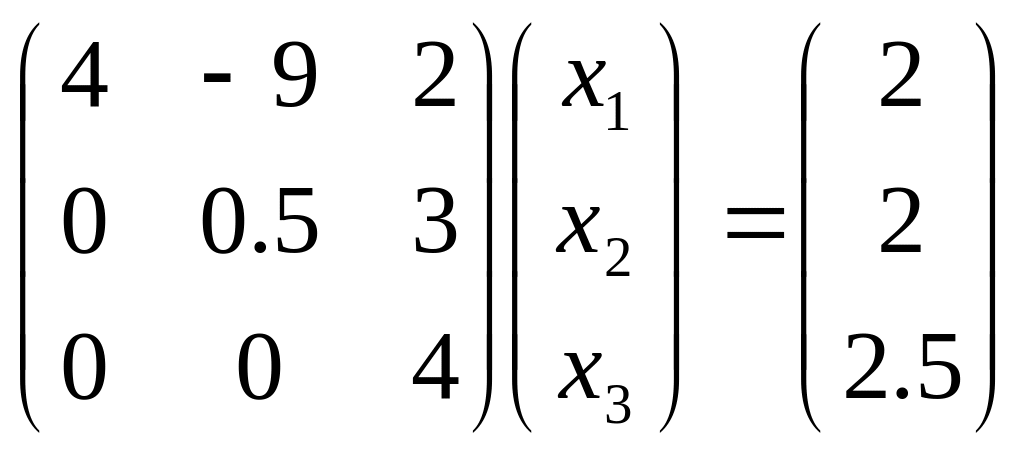
Полученную систему переписываем в привычном виде:
Теперь, из этой системы можем находить решение в обратном порядке, т.е. сначала находим из третьего уравнения x3 = 0,625, далее, подставляя во второе уравнение, находим
. Подставляя x2 и x3 в первое уравнение системы, находим x1 = 0,75. Нахождение решения x1, x2, x3 называют обратным ходом.
Метод обратной матрицы
Пусть задана система
.
Если определитель матрицы А отличен от
0, то решение может быть найдено с помощью
обратной матрицы.
Решить систему:
Решение приведено на рис.1. и 2.
Рис.1 Решение системы линейных уравнений в режиме отображения данных.
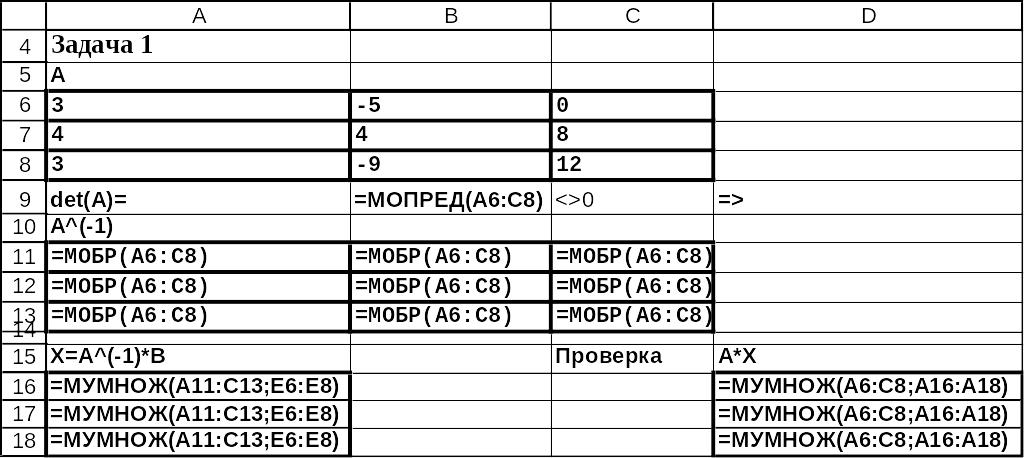
Рис.2 Решение системы линейных уравнений в режиме Отображения формул.
Таблица 1
Решить систему линейных уравнений
№ |
Задание |
|
|
8.3 x4 + 2.62 x3 + 4.10 x2 + 1.9 x1 = -10.65 3.92 x4 + 8.45 x3 + 7.78 x2 + 2.46 x1 = 12.21 3.77 x4 + 7.21 x3 + 8.04 x2 + 2.28 x1 = 15.45 2.21 x4 + 3.65 x3 + 1.69 x2 + 6.99 x1 = -8.35 |
|
|
7.5 x4 + 2.6 x3 + 1.3 x2 + 8.1 x1 = 5.7 6.4 x4 + 3.3 x3 - 2.4 x2 + 1.7 x1 = -2.1 0.1 x4 - 2.3 x3 + 0.8 x2 - 5.7 x1 = 4.6 8.2 x4 + 0.1 x3 - 5.3 x2 - 7.6 x1 = 5.1 |
|
|
6.5 x4 + 3.8 x3 - 4.1 x2 + 1.2 x1 = 9.92 7.1 x4 - 2.7 x3 - 1.4 x2 + 1.4 x1 = 6.95 -1.8 x4 - x3 + 4.3 x2 + 1.3 x1 = 7.91 1.5 x4 - 3.4 x3 + 7.8 x2 - 1.8 x1 = 15.09 |
|
|
-3.0 x4 + 2.0 x3 - 4.0 x2 + 5.0 x1 = 12.29 2.0 x4 - x3 + x2 - 11.5 x1 = -12.69 x4 - 3.0 x3 - 2.0 x2 + 2.7 x1 = 13.10 5.0 x4 - x3 + 3.0 x2 + 7.8 x1 = 56.93 |
|
|
6.0 x4 - x3 - x2 + 11.2 x1 = 26.25 - x4 - 6.0 x3 - x2 + 5.7 x1 = 39.59 - x4 - x3 + 6.0 x2 + 3.4 x1 = 46.53 2.0 x4 - x3 + 3.0 x2 - 1.4 x1 = 10.22 |
|
|
0.7 x4 - x3 + 3.0 x2 + 4.0 x1 = 0.09 x4 + x3 - 8.0 x2 + 24.0 x1 = 10.11 3.0 x4 - 0.5 x3 - 2.4 x2 + 8.75 x1 = 1.01 8.0 x4 + 7.0 x3 - 0.7 x2 + 10.1 x1 = 0.92 |
|
|
x4 - 6.0 x3 + 12.0 x2 - 5.0 x1 = 7.12 -3.0 x4 + 7.0 x3 + 2.0 x2 – x1 = 7.89 6.0 x4 - 5.0 x3 - 4.0 x2 + x1 = 9.38 x4 + 2.0 x3 - x2 + x1 = 11.19 |
|
|
x4 - 3.0 x3 + 4.0 x2 + 5.0 x1 = 7.94 -3.0 x4 + 2.0 x3 - x2 + 3.0 x1 = 1.86 -2.0 x4 + 3.0 x3 + 2.0 x2 = -3.89 4.0 x4 - x3 - 4.0 x2 - 6.0 x1 = 15.54 |
|
|
2.0 x4 + x3 - x2 = 7.44 3.0 x4 + 2.0 x3 - 4.0 x2 + 9.0 x1 = 0.87 3.0 x4 - 2.0 x3 - 2.0 x2 + 3.0 x1 = 4.85 2.0 x3 + x2 - 5.0 x1 = 9.45 |
|
|
5.0 x4 + 4.0 x2 + x1 = -1.38 2.0 x4 + 3.0 x3 - 4.0 x2 + 2.0 x1 = 0.34 -x4 + 2.0 x3 + x2 + 3.0 x1 = -4.99 x4 + 4.0 x3 - 2.0 x2 = 1.88 |
|
|
-1.2 x4 + 6.0 x3 + 9.0 x2 + 1.1 x1= 1.1 6.1 x4 + 3.7 x3 - 6.1 x2 + 7.6 x1 = 7.02 -9.2 x4 + 6.1 x3 + 13.1 x2 + 1.6 x1 = 12.9 11.1 x4 + 7.6 x3 + 16.9 x2 - 2.8 x1 = 15.6 |
|
|
4.0 x4 + 2.0 x3 + 6.3 x2 + 8.0 x1 = -1.82 2.1 x4 + 5.2 x3 - 5.3 x2 + x1 = 2.39 -6.2 x4 + 5.1 x3 + 1.4 x2 + 1.7 x1 = -4.28 8.1 x4 + 0.1 x3 + 1.7 x2 + 3.0 x1 = 6.81 |
|
|
- x4 - 6.0 x3 - x2 + 5.7 x1 = 39.59 - x4 - x3 + 6.0 x2 + 3.4 x1 = 46.53 6.0 x4 - x3 - x2 + 11.2 x1 = 26.25 2.0 x4 - x3 + 3.0 x2 - 1.4 x1 = 10.22 |
|
|
-3.0 x4 + 2.0 x3 - x2 + 3.0 x1 = 1.86 -2.0 x4 + 3.0 x3 + 2.0 x2 = -3.89 x4 - 3.0 x3 + 4.0 x2 + 5.0 x1 = 7.94 4.0 x4 - x3 - 4.0 x2 - 6.0 x1 = 15.54 |
|
|
11.1 x4 + 7.6 x3 + 16.9 x2 - 2.8 x1 = 15.6 -1.2 x4 + 6.0 x3 + 9.0 x2 + 1.1 x1= 1.1 6.1 x4 + 3.7 x3 - 6.1 x2 + 7.6 x1 = 7.02 -9.2 x4 + 6.1 x3 + 13.1 x2 + 1.6 x1 = 12.9 |
|
|
-9.2 x4 + 6.1 x3 + 13.1 x2 + 1.6 x1 = 12.9 6.1 x4 + 3.7 x3 - 6.1 x2 + 7.6 x1 = 7.02 11.1 x4 + 7.6 x3 + 16.9 x2 - 2.8 x1 = 15.6 -1.2 x4 + 6.0 x3 + 9.0 x2 + 1.1 x1= 1.1 |
2.Решение нелинейного уравнения