2. Кинематические цепи и их классификация. Степень подвижности кинематической цепи

Связанную систему звеньев, образующих кинематические пары, называют кинематической цепью. Цепи делят на открытые и замкнутые, простые и сложные, плоские и пространственные.

В открытой цепи имеются звенья, входящие только в одну кинематическую пару (рис. 2.1, а). В замкнутой цепи каждое звено входит не менее чем в две кинематические пары (рис. 2.1, б). Кинематическую цепь называют простой, если каждое ее звено (1-4) входит не более чем в две кинематические пары (рис. 2.1, в). В сложной цепи имеется хотя бы одно звено, образующее с другими звеньями более двух кинематических пар (рис. 2.1,б). Если траектории точек всех звеньев цепи лежат в параллельных плоскостях, то такую цепь называют плоской. В пространственных цепях указанные траектории либо представляют собой пространственные кривые, либо находятся в непараллельных плоскостях.

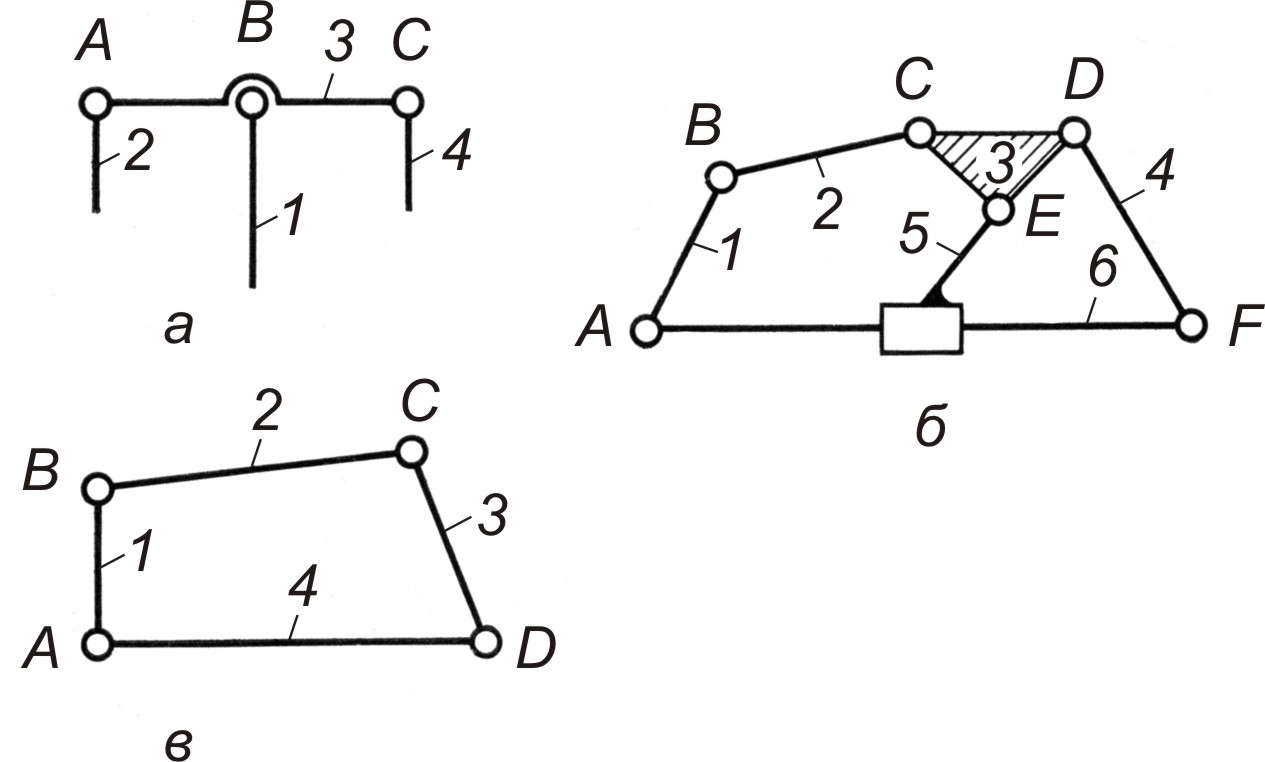
Рис. 2.1. Кинематические цепи:

а – открытая; б, в – замкнутые

Число степеней свободы кинематической цепи относительно одного из ее звеньев условно называют степенью ее подвижности. Для определения степени подвижности любой кинематической цепи необходимо подсчитать число степеней свободы всех подвижных звеньев, полагая их не связанными между собой. Затем из этого числа следует вычесть число связей, наложенных на звенья кинематическими парами. Пусть n – число звеньев пространственной кинематической цепи, p_k – число кинематических пар k-го класса (k=1,2,…,5). Общее число степеней свободы n звеньев без учета связей равно 6n, а общее число связей, наложенных на звенья кинематическими парами k-го класса, равно kp_k. Поэтому степень подвижности кинематической цепи

,

или в развернутом виде

. (2.1)

Равенство (2.1) носит название формулы подвижности или структурной формулы пространственной кинематической цепи общего вида (формула Сомова-Малышева).

Связи, налагаемые на движение звеньев кинематическими парами, подразделяют на индивидуальные, характерные для данного звена цепи, и общие, накладывающие одинаковые ограничения на движение всех звеньев. Например, кинематическая цепь (рис. 2.1, в), звеня которой соединены между собой с помощью лишь вращательных пар V класса с параллельными осями, является плоской. Звенья такой цепи движутся параллельно некоторой направляющей плоскости, перпендикулярной к осям вращательных пар. Следовательно, все звенья цепи не могут перемещаться вдоль оси, перпендикулярной к направляющей плоскости, и вращаться вокруг двух осей, определяющих эту плоскость, т.е. на звенья данной цепи наложены три общие связи. Структурная формула (2.1) в этом случае не применима. Число степеней свободы отдельно взятого звена такой цепи с учетом лишь общих связей равно трем, а n звеньев – 3n. Однако каждая пара ограничивает движение звеньев дополнительными связями, число которых для рассматриваемой цепи на три единицы меньше класса пары. Следовательно, кинематические пары I, II и III классов в одной цепи не могут иметь места, а пары IV и V классов накладывают соответственно одну и две связи. Таким образом, в этом случае имеет место формула Чебышева:

. (2.2)

Структурные формулы для кинематических цепей с другим числом общих связей могут быть получены по аналогии с формулой (2.2).