2. Основы теории механизмов

1. Механизм и машина

Машина - искусственное устройство, выполняющее механические движения для преобразования энергии, материалов и информации и служащие для облегчения физического и умственного труда человека, увеличения его производительности и расширения производственных возможностей. Использование какой-либо формы движения и совершение полезной работы являются признаками машины. Этим она отличается от сооружений и приборов (приборы служат для регистрации параметров физических процессов, осуществления технических измерений, но не для совершения работы).

По функциональному назначению различают:

• машины-двигатели, преобразующие один вид энергии в другой (двигатели внутреннего сгорания, электродвигатели);

• транспортные машины, осуществляющие перемещение тел (автомобили, конвейеры);

• технологические или рабочие машины, изменяющие состояние, свойства или форму материала (мельницы):

• вычислительные машины (ЭВМ);

• контрольно-управляющие машины.

Понятие механизм является более широким, чем понятие машина, прибор, приспособление. Всякое из названных устройств является одновременно механизмом.

Механизм - искусственно созданная механическая система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел (в соответствии с функциями устройства, основой которой является эта система).

Твердые тела, входящие в состав механизма, и обладающие относительной подвижностью, называются звеньями механизма. Звенья состоят из одной или нескольких жестко связанных между собой частей - деталей.

Для звена характерным является форма геометрических элементов и их взаимное расположение, поскольку именно эти факторы определяют вид относительного движения звеньев. Другие параметры (материал, способ изготовления) в теории машин и механизмов не рассматриваются.

Различают звенья:

• жесткие (физические свойства не зависят от действующих на звено сил; например, шатун, зубчатое колесо, поршень, коленчатый вал),

• упругие (пружины, рессоры, металло-резиновые соединения),

• гибкие (канаты, ремни, цепи).

Жидкости и газы в теории механизмов звеньями не считаются.

Звенья, к которым приложены силы, приводящие механизм в движение, называют ведущими. Все остальные звенья - ведомые. Неподвижное звено называют стойкой.

1. Кинематические пары и их классификация

Чтобы разобраться в структуре механизма, надо рассматривать не отдельно взятые звенья, но и характер их соединения. При этом следует интересоваться лишь кинематическими возможностями звеньев совершать определенные движения и не принимать во внимание их конструктивные особенности.

Кинематическая пара - подвижное соединение двух соседних соприкасающихся звеньев (другими словами, кинематическую пару образуют два звена при условии их соприкосновения и возможности относительного движения). Такую пару могут образовать не только подвижные звенья, но и звенья, одно из которых неподвижно и служит в механизме стойкой.

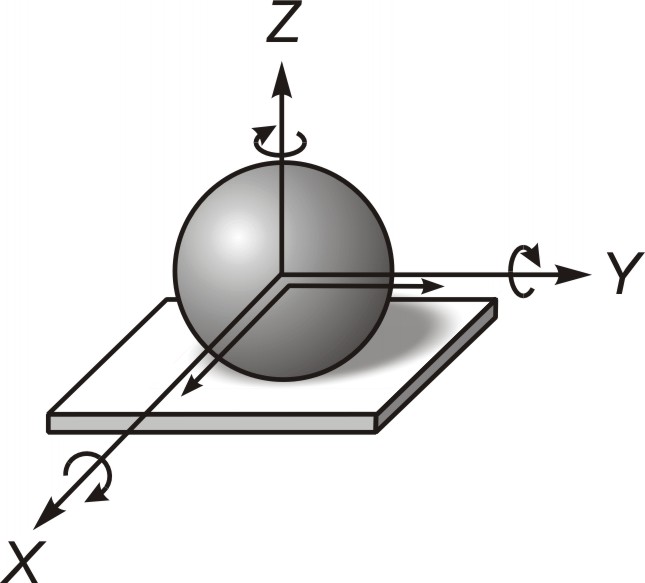
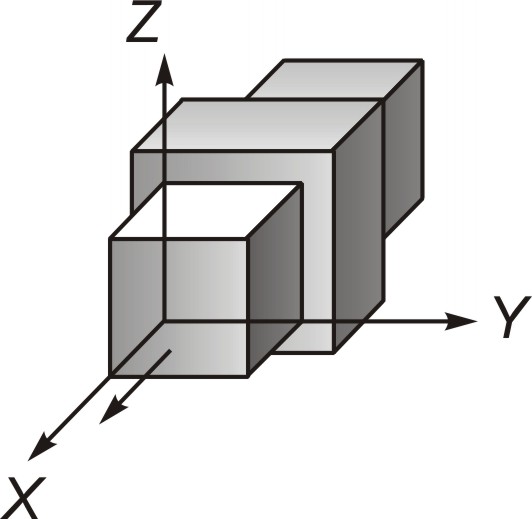
Если рассматривать звено свободно движущимся в пространстве, то оно, как любое изолированное твердое тело, обладает шестью степенями свободы, каждая из которых определяется изменением одной обобщенной координаты (любые независимые друг от друга параметры, однозначно определяющие положение данного тела или вообще механической системы). Изменениям обобщенных координат свободного звена в пространстве соответствуют три поступательных (ППП) перемещения вдоль координатных осей x, y и z и три вращательных (ВВВ) движения вокруг тех же осей (рис. 2.1).

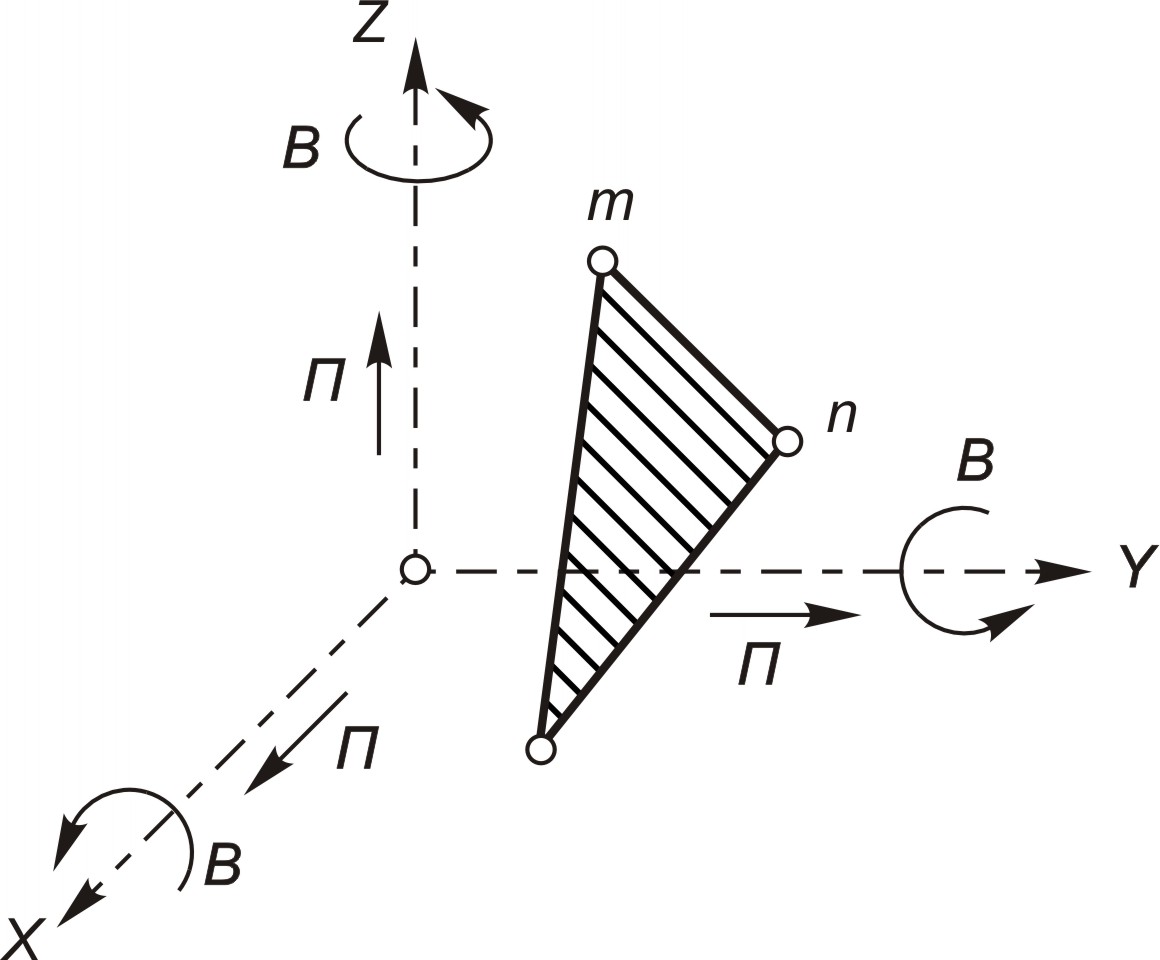
Рис. 2.1. Изменение обобщенных координат

свободного звена в пространстве

Любая кинематическая пара ограничивает движение звеньев, исключая те или иные движения из шести возможных (ПППВВВ). В этом заключается одно из главных свойств кинематических пар. Ограничения, налагаемые на движение звеньев, называют связями. В зависимости от числа связей кинематические пары разделяют на классы (классификация И.И.Артоболевского).

Сколько же степеней свободы может быть в кинематических парах? Если тело, обладающее шестью степенями свободы, вступает в кинематическую пару (в соприкосновение) с другим телом, то минимум одно движение у него ограничивается (движение в направлении общей нормали к поверхностям звеньев в точке их соприкосновения) - на это движение накладывается условие связи. Следовательно, кинематическая пара может иметь максимум пять степеней свободы. Минимально кинематическая пара может иметь одну степень свободы, так как если степень свободы будет равна нулю, то это будет не кинематическая пара, а неподвижное соединение звеньев.

Любую кинематическую пару можно отнести к одному из возможных пяти классов, имея в виду, что номер класса совпадает с числом связей, налагаемых парой.

Рассмотрим кинематические пары всех пяти классов (табл. 2.1). Какие возможные перемещения, сохранили звенья после образования пары.

Таблица 2.1

Классификация кинематических пар

Класс пары	Число связей	Число степеней свободы	Примеры кинематических пар	Класс пары	Число связей	Число степеней свободы	Примеры кинематических пар
1	2	3	4	5	6	7	8
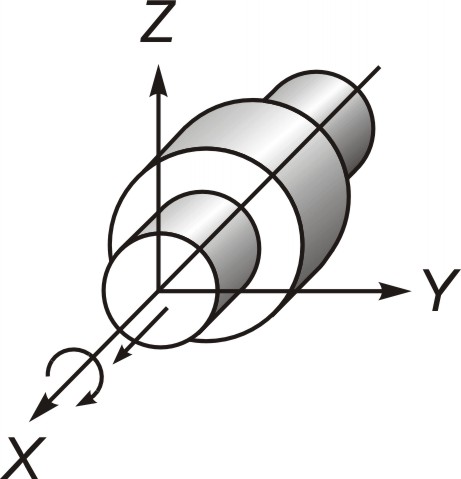
I	s=1	w=5	Шар на плоскости	IV	s=4	w=2	Цилиндрическая пара

Окончание табл. 2.1

1	2	3	4	5	6	7	8
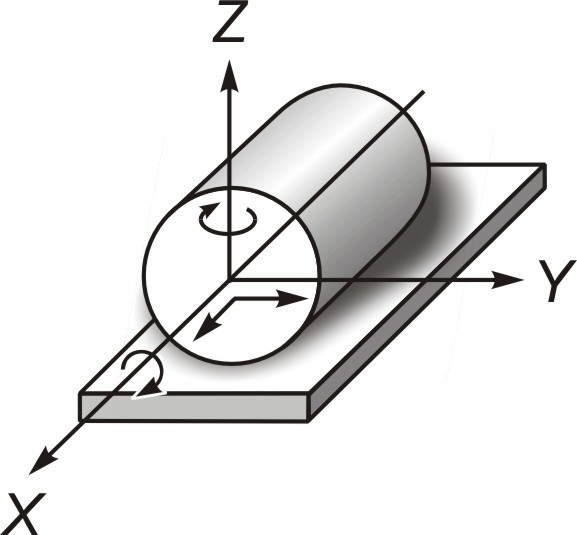
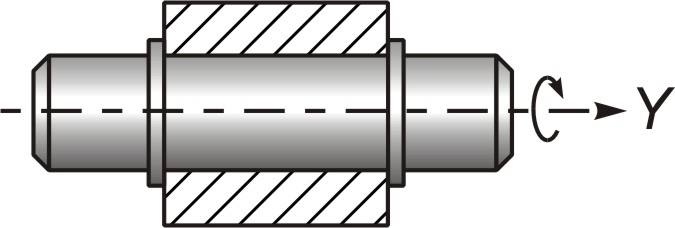
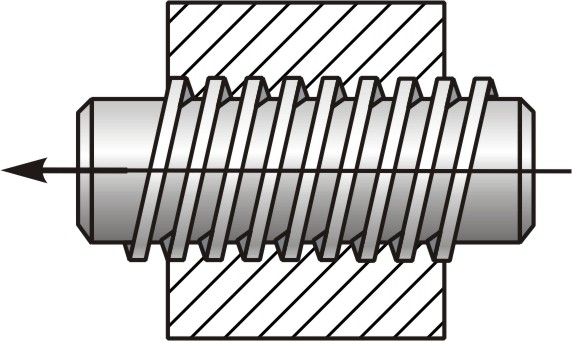
II	s=2	w=4	Цилиндр на плоскости	V	s=5	w=1	Вращательная пара Поступательная пара Винтовая пара
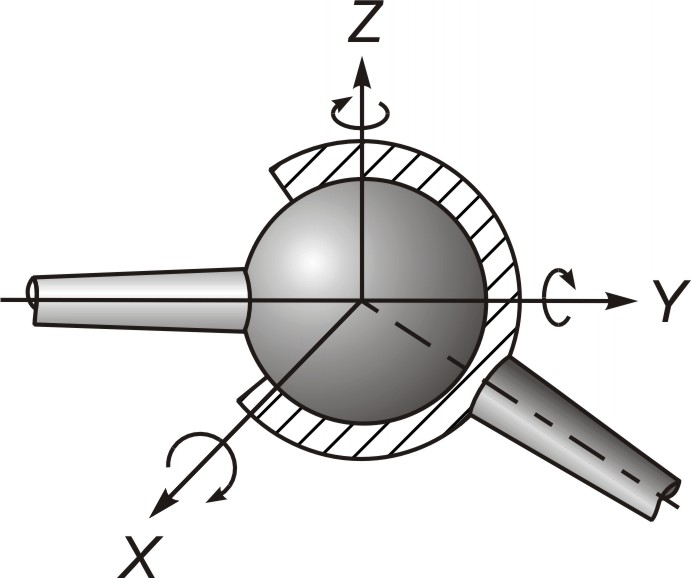
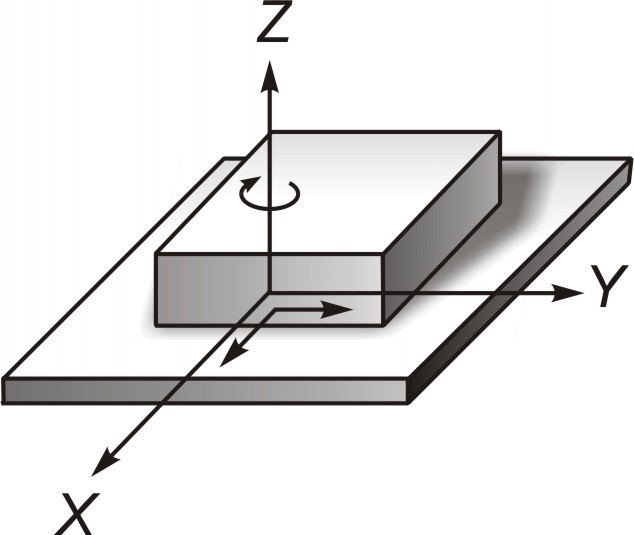
III	s=3	w=3	Сферический шарнир Плоская пара

Сферическая пара допускает три независимых относительных вращения звеньев вокруг осей x, y, z.

Поступательная пара допускает лишь прямолинейное поступательное относительное движение звеньев.

Вращательная пара допускает лишь относительное вращательное движение звеньев вокруг оси.

В современных механизмах применяют преимущественно кинематические пары III, IV и V классов.

Если допустить, что на форму контакта соприкасающихся твердых тел их деформации влияния не оказывают, то звенья пары могут иметь соприкосновение: 1) по поверхности, 2) по линии или в точке. В первом случае пары называют низшими, во втором – высшими.

В табл. 2.1 приведены две высшие кинематические пары. Для одной из них (шар на плоскости) формой контакта является точка, а для другой (цилиндр на плоскости) – линия.

Одним из положительных качеств низших кинематических пар является их способность передавать значительную нагрузку от одного звена другому, так как звенья этих пар соприкасаются по поверхности. Нагрузочная способность высших кинематических пар сравнительно не велика, поскольку усилия в ней передаются через малые контактные площадки, возникающие в местах соприкосновения звеньев под воздействием нагрузок.

Механизмами с высшими парами являются зубчатые передачи, кулачковые, фрикционные, мальтийские и храповые механизмы.

В процессе движения звеньев механизма между их геометрическими элементами необходим постоянный контакт. Замыкание кинематических пар может быть либо геометрическим, либо силовым. Первое достигается за счет формы геометрических элементов звеньев. Такие пары называют закрытыми (например, винтовая пара). Второе обеспечивается силами тяжести звеньев, упругостью пружин и т.д. Пары с таким замыканием называют открытыми (например, шар на плоскости).

Кинематическая пара является обратимой, если она реализует один и тот же вид относительного движения для каждого из образующих ее звеньев. Примером обратимой может служить вращательная пара. Действительно, вращение вала в неподвижном подшипнике или подшипника относительно вала приводит к тому, что точки соприкасающихся поверхностей вала и подшипника описывают одинаковые траектории – окружности. Свойством обратимости обладают все низшие кинематические пары. Все высшие кинематические пары относятся к необратимым.

Пользуясь условными изображениями наиболее распространенных кинематических пар, компонуют так называемые структурные схемы механизмов. Структурная схема представляет собой символический чертеж механизма, позволяющий установить количество его звеньев, число и класс кинематических пар, а также вид движения, которое совершает каждое звено относительно стойки. Выполненную в масштабе структурную схему называют кинематической.