Продольный изгиб
Рассматривая деформацию сжатия, мы отмечали, что она возникает при действии на брус сил, направленных по его продольной оси навстречу друг другу, и что при этом поперечные размеры бруса мало отличаются от его продольных размеров.
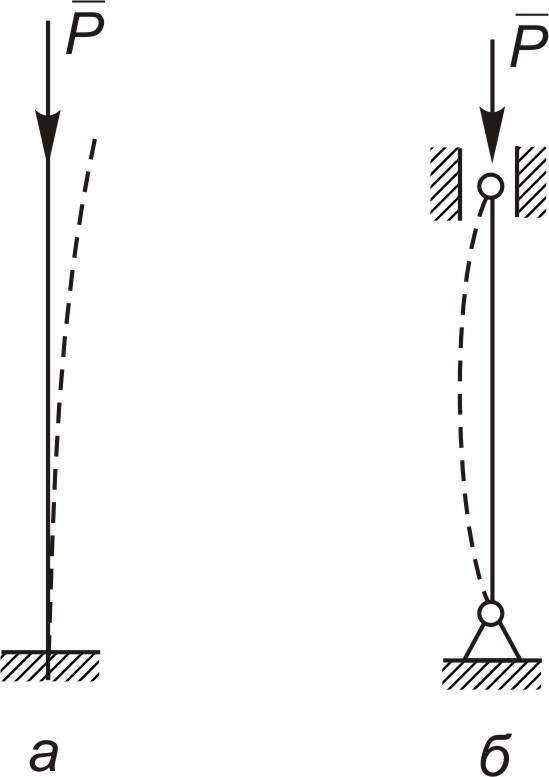
Если поперечные размеры бруса будут во много раз меньше его длины (такой брус называют стержнем), то может возникнуть иное напряженное состояние. Вначале, когда силы невелики, стержень действительно подвергается сжатию и его ось будет оставаться прямолинейной. Однако, увеличивая силу, можно подойти к такому ее значению, которое выведет стержень из устойчивого положения — его ось станет криволинейной (рис. 3.14). Естественно, что работоспособность детали при этом будет нарушена. Деформация стержня, являющаяся следствием потери его устойчивости под действием сжимающих сил, называется продольным изгибом.
Рис. 3.14. Продольный изгиб стержней жестко закрепленного (а) и с шарнирными опорами (б) |
Сила, которая соответствует моменту перехода стержня из устойчивого положения в неустойчивое, называется критической силой, а напряжение сжатия, соответствующее этой критической силе, называется критическим напряжением. Практика показывает, что это напряжение меньше обычного предельно опасного напряжения, ориентируясь на которое выбирают допускаемые напряжения при сжатии. Поэтому, чтобы расчет на прочность при сжатии одновременно гарантировал устойчивость, допускаемые напряжения на сжатие при таком нагружении стержней снижаются в зависимости от соотношения длины и поперечных размеров стержня и от способа закрепления его концов. Например, стержень, закрепленный, как показано на рис. 3.14, а, менее устойчив, чем стержень, показанный на рис. 3.14, б.
|
Задачи с решениями
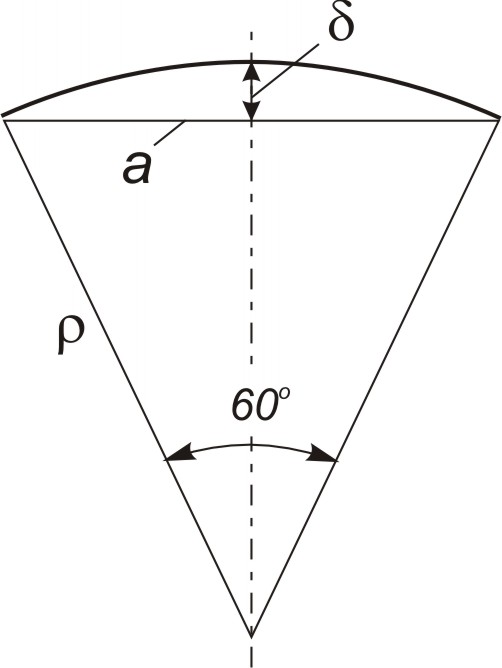
Задача 1. Стальная линейка, имеющая поперечное сечение hXb 1X25 мм и длину l=250 мм, изгибается парами сил, приложенными в концах ее так, что она обращается в дугу круга с центральным углом 60о. Найти наибольшее напряжение и прогиб (рисунок).
Для стали Е=2,1∙105 МПа.
|
Решение. Радиус кривизны определяется из уравнения
где l – длина дуги;
Величина наибольшего напряжения вычисляется по формуле
|
,
.
;
.
Прогиб, вычисляемый как стрелка дуги круга,
.
Задача 2. Найти наибольшее напряжение в стальной линейке, имеющей поперечное сечение 1X25 мм и длину l=250 мм, если наибольший прогиб по середине равен 25 мм.
Для стали Е=2,1∙105 МПа.
Решение.
.
Для сегмента круга:
длина дуги
;
(1)
хорда
. (2)
Из уравнения (1)
.
Подставив а в уравнение (2), получим
;
.