3. Расчеты на прочность при изгибе

При проектном расчете требуется определить минимальные размеры опасного поперечного сечения, которые обеспечат при заданной нагрузке необходимую прочность. Изгибающий момент в опасном сечении и материал балки (следовательно, допускаемые напряжения тоже) известны. Как и в случае других деформаций, расчет ведут в предположении, что максимальные действительные напряжения будут равны или несколько меньше допускаемых, т. е.

,

откуда

.

Затем в зависимости от предполагаемой формы поперечного сечения балки определяют его необходимые размеры. Если сечение балки круглое, то W = 0,1 d ³, откуда находится искомый диаметр d. Если же сечение балки представляет собой квадрат со стороной а, то искомый размер находят из равенства

.

Несколько сложнее определить размеры прямоугольного сечения балки. В этом случае необходимо знать ориентацию сечения по отношению к действующему моменту, т. е. надо знать положение нейтральной оси. Знание положения нейтральной оси позволит из двух зависимостей , выбрать необходимую. Однако определить величины b и h можно будет лишь при условии, если известно отношение . Если сечение представляет собой стандартный профиль (двутавр, швеллер), то по полученной в расчете величине W из справочных таблиц подбирают номер соответствующего профиля. Причем табличное значение W_табл должно быть больше расчетной величины W или равно ей.

При проверочном расчете определяют максимальные действительные напряжения, т. е. напряжения в наиболее опасных точках опасного сечения, и сравнивают их с допускаемыми. В этом случае предварительно находят изгибающий момент в опасном сечении и допускаемые напряжения:

.

4. Определение опасного сечения при изгибе

Выше отмечалось, что одно из отличий деформации изгиба от деформации растяжения (при рассмотренных нами случаях нагружения) — наличие опасного сечения, т. е. сечения, в котором действует максимальный изгибающий момент. Очевидно, надо научиться определять положение опасного сечения балки и изгибающий момент в этом сечении.

Мы уже анализировали простейший случай нагружения балки (рис. 3.10) и нашли положение опасного сечения, опираясь лишь на опыт. Снова вернемся к этому случаю и приведем более строгие доказательства. Балку теперь изобразим упрощенно (рис. 3.12, а). Для определения внутренних силовых факторов воспользуемся методом сечений. Так как этот метод применим лишь к свободному телу, то будем рассматривать равновесие отсеченной правой части (рис. 3.12, б). В сечении 1 будут действовать поперечная сила Q = Р и изгибающий момент M_и== Px₁. Рассмотрим теперь сечение 2 (рис. 3.12, в). В нем будет действовать та же сила Q, но момент будет другой — Рх₂. Аналогичные результаты получим и для других сечений. Мы уже условились, что поперечными силами и вызванными ими касательными напряжениями сдвига будем пренебрегать. Все внимание сосредоточим на изгибающем моменте, величина которого, как это ясно из предыдущих рассуждений, изменяется по длине балки по линейному закону — пропорционально отрезкам x₁, x₂ и т. д.

Этот закон можно изобразить графически — построить так называемую эпюру (график изменения) моментов. Выбрав масштаб для единицы момента, откладываем от осевой линии эпюры (рис. 3.12, г) ординату, соответствующую величине наибольшего момента равного Рl (условимся момент считать положительным, если он прогибает балку выпуклостью вниз; следовательно, в данном случае момент отрицательный).

Вторая точка для построения графика соответствует свободному концу балки. В этом сечении момент равен нулю. Соединив точки а и б, получим график изменения изгибающего момента по длине балки, т. е. эпюру моментов. Промежуточные между точками а и б ординаты соответствуют моментам в соответствующих сечениях. Итак, для данного случая получили, что опасное сечение — в заделке, а изгибающий момент в нем равен Рl.

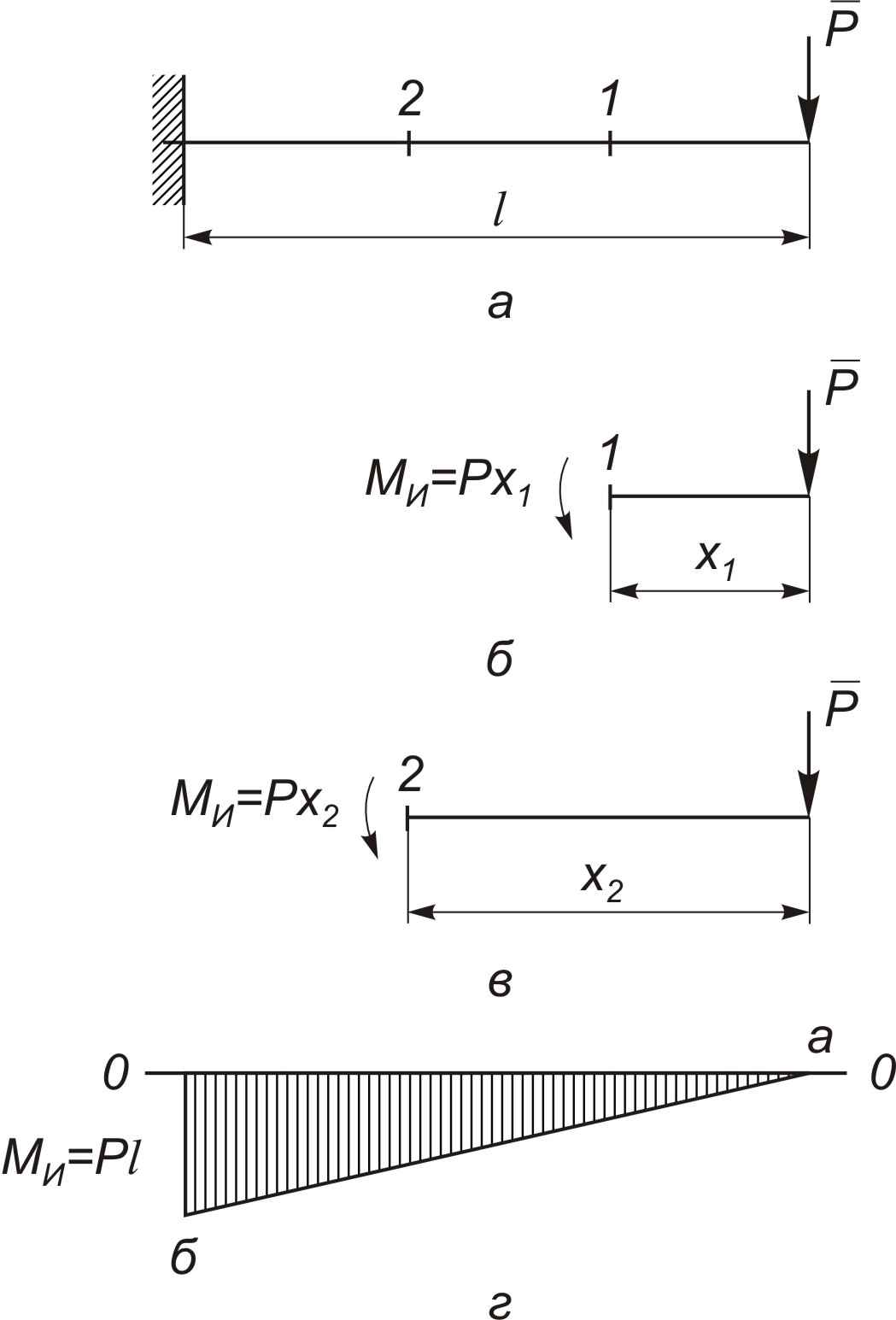
Рис. 3.12. Построение эпюры изгибающих моментов

для одноопорной (консольной) балки:

а – схема действия внешней силы; б, в – равновесие отсеченных частей; г – эпюра изгибающих моментов

Разберем более сложный случай, когда балка двухопорная и нагружена силой в середине пролета (рис. 3.13, а). Здесь сразу нельзя применить метод сечений, так как по любую сторону от сечения оказывается несвободная часть балки со связями. В подобных случаях надо вначале отбросить опоры и заменить их реакциями (рис. 3.13, б). Каждая из реакций равна .

Применяя многократно метод сечений, вначале рассмотрим равновесие отсеченных частей балки, расположенных правее любого из сечений, проведенных на участке от правого конца балки до середины пролета. Результат очевиден: если на конце балки момент равен нулю, то к середине пролета он возрастает до значения , т.е. . Затем точно так же рассмотрим равновесие отсеченных частей балки, расположенных левее любого из сечений, проведенных на участке от левого конца балки до середины пролета. Результаты будут аналогичными. Выбрав масштаб единицы момента и установив, что изгибающий момент положителен, отложим вверх по оси ординату и построим эпюру М_и (рис. 3.13, в). По эпюре видно, что в данном случае опасное сечение находится в середине пролета, а момент М_и в опасном сечении равен . Именно эту величину надо будет подставить в расчетное уравнение при проектном или проверочном расчете балки на изгиб.

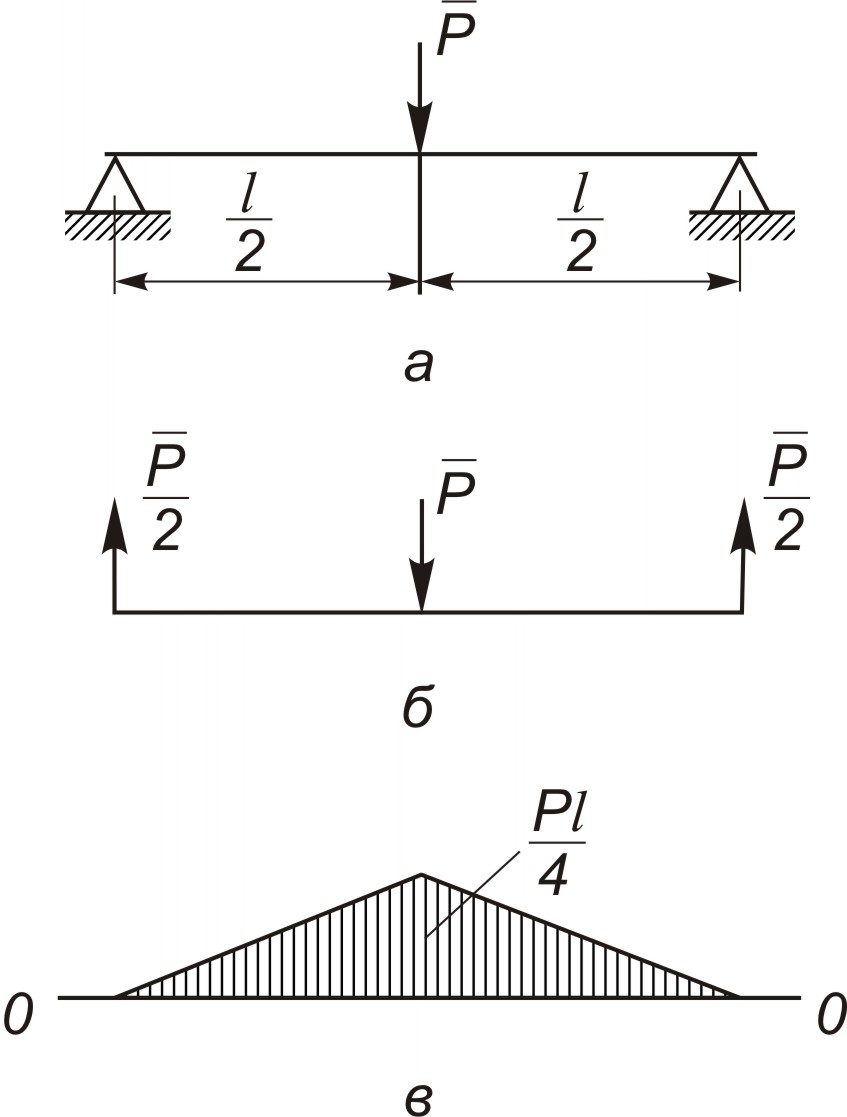
Рис. 3.13. Построение эпюры изгибающих моментов

для двухопорной балки:

а – схема действия внешней силы, б – равновесие балки под действием внешней силы и опорных реакций, в – эпюра изгибающих моментов