1. Расчеты на прочность при сдвиге (срезе)

Расчет на прочность при сдвиге ничем не отличается от расчета на прочность при растяжении (сжатии). Так при проектном расчете

,

откуда

.

При проверочном расчете

.

2. Задачи с решениями

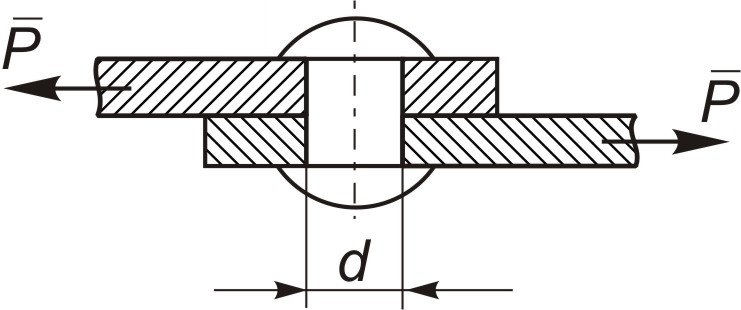
Задача 1. Два листа соединены заклепкой. На соединение действуют силы Р=5 кН. Определить, достаточна ли прочность заклепки, если ее диаметр d=15 мм, а [ср]=50 МПа (рисунок).

Решение

1. Определим внешние силы, действующие на заклепку. Силы Р действуют в параллельных плоскостях на очень малом расстоянии друг от друга и направлены в противоположные стороны.

2. Определим внутренние силы, действующие в заклепке. Нетрудно заметить, что единственным сечением заклепки, в котором возможна деформация (исключая деформацию смятия на боковых поверхностях), является сечение, совпадающее со стыком листов. Применив метод сечения, выясняем, что равнодействующая внутренних сил Q=P, а сами силы ориентированы так, что появляются касательные напряжения сдвига.

3. Проверим прочность заклепки. Прочность заклепки будет достаточной, если возникающие в ней действительные напряжения сдвига не превысят допускаемых.

Действительные напряжения

; ;

.

Так как , то прочность заклепки достаточна.

4. Кручение

С кручением на практике приходится встречаться очень часто: трансмиссионные валы, элементы пространственных конструкций и даже обыкновенный замочный ключ.

Рассмотрим сначала задачу о скручивании валов круглого поперечного сечения.

Деформация кручения вызывается парами сил, лежащими в плоскостях, перпендикулярных к оси стержня.

Момент сил, скручивающих вал, называется крутящим моментом.

Деформация кручения возникает при действии на брус нагрузок, создающих противоположные пары сил в плоскостях, перпендикулярных продольной оси бруса. Например, при кручении круглого бруса каждое поперечное сечение по отношению к соседнему поворачивается на некоторый угол, прямолинейные образующие принимают вид винтовых линий.

Можно представить себе и другую картину: брус сложен из множества тончайших дисков. При повороте каждого диска на стыке с соседним происходят перемещения точек в плоскостях, перпендикулярных оси бруса. Отсюда вывод – при кручении бруса в каждом сечении происходит деформация сдвига и возникают касательные напряжения. Однако если при обычном сдвиге все точки деформируемого сечения прямолинейно смещались на равные расстояния, то при кручении материал в разных точках, находящихся на разных расстояниях от оси бруса, испытывает разную деформацию.

Чем дальше точка удалена от оси, тем больше перемещение по дуге. Но так как величина напряжений прямо пропорциональна относительной деформации (по закону Гука), то очевидно, что и напряжения в различных точках одного и того же сечения будут различны и пропорциональны расстоянию точки от центра сечения (его называют полюсом). В точке сечения, совпадающей с полюсом, напряжение равно нулю. Наибольшие напряжения _max будут в наиболее удаленных точках, расположенных на поверхности бруса. Таким образом, первое отличие деформации кручения от деформации сдвига заключается в различных законах распределения напряжений по сечению.

При сдвиге действительные напряжения определялись делением равнодействующей внутренних сил упругости на площадь поперечного сечения (аналогично для растяжения, сжатия и смятия). Для определения действительных напряжений при кручении так поступать нельзя – изменился внутренний силовой фактор (вместо силы – момент) и стал другим закон распределения напряжений по сечению (вместо равномерного – неравномерное). Вывод расчетной формулы для определения действительных напряжений в опасных точках сечения скручиваемого бруса, т.е. для определения _max, достаточно сложен и требует большого числа математических преобразований.

Соответствующие приведенным рассуждениям математические преобразования (при условии, что брус имел круглое поперечное сечение с диаметром d) приводят к следующей формуле:

,

где – полярный момент сопротивления сечения кручению, м³. Для практических расчетов можно принять, что . Величина W_р характеризует способность круглого поперечного сечения заданных размеров сопротивляться деформации кручения.