3. Понятие о деформациях и напряжениях

Как элементы конструкций, так и конструкции в целом при действии внешних сил в большей или меньшей степени изменяют свои размеры и форму и в конце концов могут разрушиться. Это изменение носит общее название – деформация.

Величины и характер деформаций связаны со структурой, строением применяемых нами материалов.

Если тело в результате приложения к нему силы изменяет форму, а после прекращения действия нагрузки восстанавливает ее, то такая деформация называется упругой. Если после снятия нагрузки тело не восстанавливает прежней формы, то говорят об остаточной (пластической) деформации.

Характер деформации (упругая или остаточная) зависит от величины действующей на тело силы, его размеров и механических свойств материала.

Деформации разделяются на упругие и остаточные. Упругими деформациями называются такие изменения формы и размеров элементов, которые исчезают после удаления вызвавших их сил, – тело полностью восстанавливает свою прежнюю форму.

Если же внешние силы перешли этот предел, то после их удаления форма и размеры элемента не восстанавливаются в первоначальном виде; оставшиеся разности размеров называются остаточными деформациями.

В элементах конструкции под действием внешних сил возникают дополнительные внутренние силы, сопровождающие деформацию материала. Эти внутренние силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну его часть от другой. Они стремятся восстановить прежнюю форму и размеры деформированной части конструкции.

Дополнительные внутренние силы в дальнейшем будем называть усилиями. Эти усилия и являются предметом нашего изучения, так как именно их величина характеризует способность тел сопротивляться внешним воздействиям.

Для определения величины внутренних усилий пользуются методом сечений, суть которого заключается в следующем.

1. Тело, на которое действует какая-либо внешняя нагрузка, в интересующем нас месте рассекается (мысленно) на две части (рис. 3.3, а).

2. Отбрасывается условно одна из частей (например, часть В).

3. Действие отброшенной части В на оставшуюся А заменяется внутренними силами.

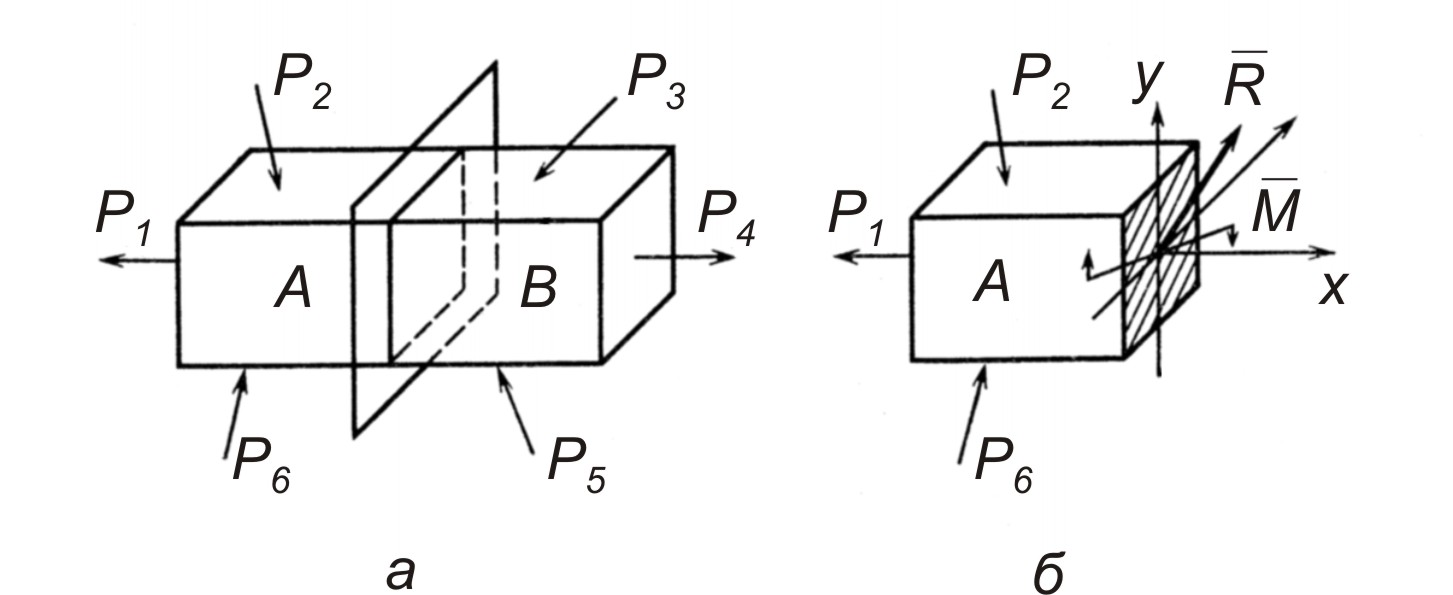
Рис. 3.3. Определение внутренних усилий

методом сечений

Так как тело под действием внешних сил находилось в состоянии статического равновесия, то эти внутренние силы, являющиеся внешними для оставшейся части, должны уравновесить часть А с приложенными к ней внешними силами (рис. 3.3, б). Таким образом, внутренние силы сводятся к категории внешних сил, для определения которых можно использовать уравнения статики твердого тела.

Со стороны отброшенной части на часть А действует система сил, распределенных по всему сечению. Эту систему в общем случае можно привести к одной силе R (главному вектору) и к одной паре сил М (главному моменту) (рис. 3.3, б). Выбрав систему координатных осей х, у, z с началом в центре тяжести сечения, разложим главный вектор и главный момент на составляющие по указанным осям. Эти составляющие имеют следующие обозначения и названия: R_x = N — продольная сила; R_y = Q_y и R_z = Q_z — поперечные силы соответственно в плоскостях ух и хz; М_.х = М_кр — крутящий момент; M_y и М_z— изгибающие моменты соответственно в плоскостях хz и ху.

Этим видам внутренних усилий соответствуют следующие виды деформации: 1) растяжение или сжатие — при появлении в поперечных сечениях только продольных усилий N; 2) сдвиг — при появлении в поперечных сечениях только поперечных усилий Q_y или О_z; 3) кручение — в поперечных сечениях возникают только крутящие моменты; 4) изгиб — в сечении действует только изгибающий момент M_y или М_z.

Появление в поперечных сечениях сразу нескольких внутренних усилий приводит к сложным видам деформации (сложному сопротивлению).

Величина напряжений в каждой точке и является мерой внутренних сил, которые возникают в материале как результат деформации, вызванной внешними силами.

Подводя итог вышесказанному заметим, что результатом действия внешних сил на элементы конструкции является возникновение в них деформаций, сопровождаемых напряжениями.

Величина внутренних сил упругости, приходящаяся на единицу площади поперечного сечения тела, называется напряжением. Иначе можно сказать, что напряжения являются мерой интенсивности распределения внутренних сил упругости.

Если вектор внутренних сил, а значит и напряжений, направлен перпендикулярно рассматриваемому сечению тела, напряжение называется нормальным и обозначается . Если напряжение действует в плоскости рассматриваемого сечения тела, то его называют касательным и обозначают .

Проиллюстрируем этот метод на трех простых случаях нагружения бруса (рис. 3.4, I, II, III). Первый шаг — рассекаем брус (рис. 3.4, б), затем отбрасываем одну часть (рис. 3.4, в) (показана оставленная часть); наконец, заменяем действие отброшенной части внутренними силами с таким расчетом, чтобы соблюдались условия равновесия, т. е. производим III и IV действия (рис. 3.4, г). В этих случаях для равновесия бруса необходимо и достаточно, чтобы внутренние силы приводились к равнодействующим (продольной или нормальной силе) или (поперечной или перерезывающей силе).

В случае I силы направлены перпендикулярно к сечению и, естественно, приводят к появлению нормальных напряжений растяжения _р. В случае II силы также направлены перпендикулярно к сечению, однако ориентированы так, что будут иметь место нормальные напряжения сжатия _с. В случае III силы действуют в плоскости сечения и поэтому появятся касательные напряжения сдвига _ср.

Теперь рассмотрим применение метода сечений еще для двух, более сложных, случаев нагружения (IV, V). Первые два действия — рассекаем брус и отбрасываем одну его часть (рис. 3.4, б,в) — ничем не отличаются от аналогичных действий в предыдущих примерах. Не отличаются и следующие два действия (рис. 3.4, г), однако результат они дадут иной. Так как брусья нагружены внешними моментами сил, то их уравновесить можно лишь равными моментами сил. Очевидно, что в сечении внутренние силы упругости в этих случаях приводятся не к равнодействующим силам, а к парам сил.

В случае IV плоскость действия равнодействующей пары внутренних сил (крутящего момента) совпадает с плоскостью сечения (плоскость действия пары сил перпендикулярна продольной оси бруса), а значит, и сами внутренние силы действуют в плоскости сечения. В итоге появятся касательные напряжения кручения _к.

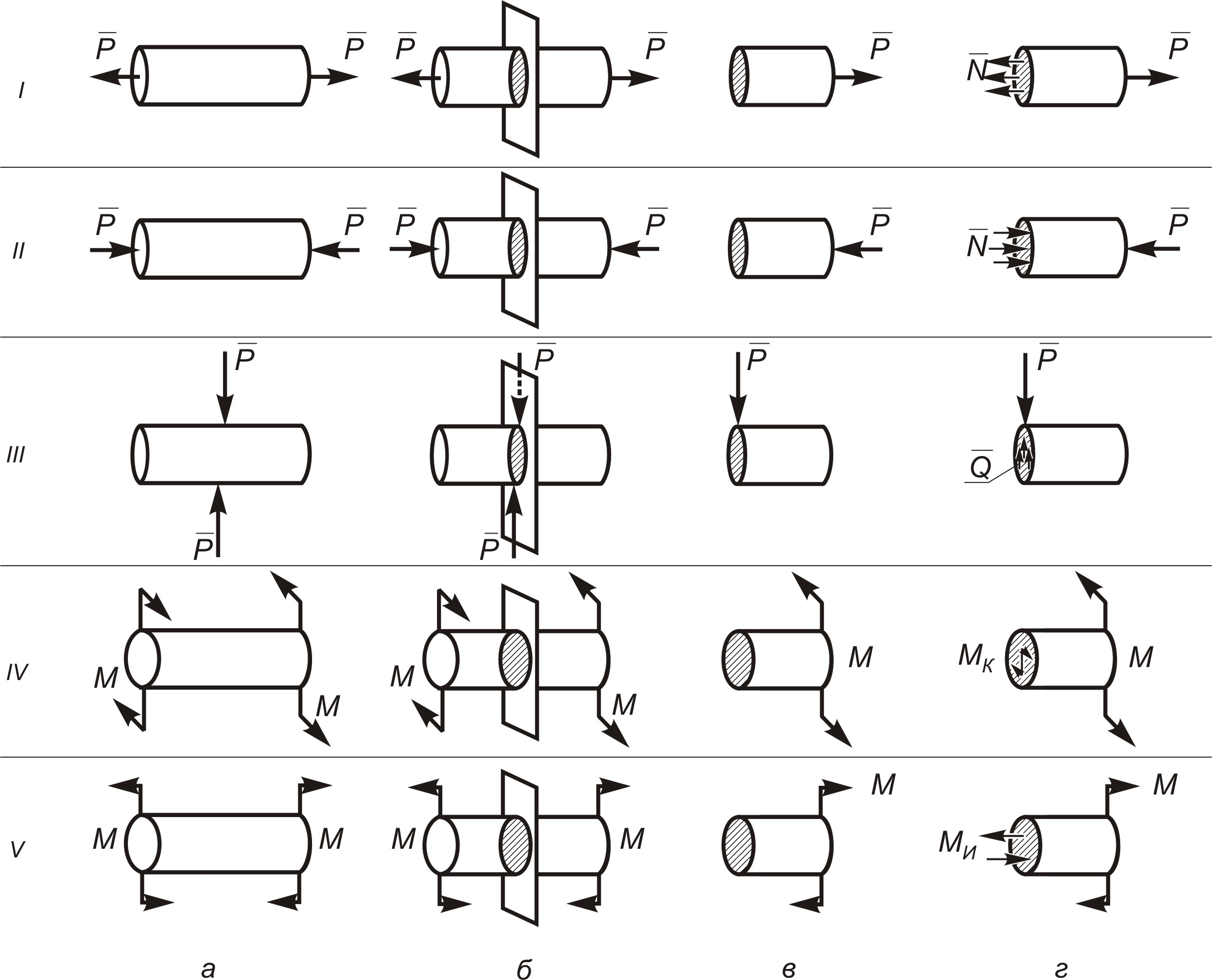
Рис. 3.4. Схемы определения внутренних сил упругости:

а – исходная схема нагружения бруса; б – брус рассекается плоскостью; в – отсеченная часть бруса;

г – равновесие отсеченной части бруса

В случае V аналогичные рассуждения позволят выявить равнодействующую пару сил (изгибающий момент), действующую в плоскости, перпендикулярной сечению и являющуюся результатом действия нормальных сил. Поэтому возникнут нормальные напряжения изгиба _и.