Зубчатые передачи
Зубчатая передача – это механизм, который с помощью зубчатого зацепления передает или преобразует движение с изменением угловых скоростей и моментов.
Зубчатые передачи применяют для преобразования и передачи вращательного движения между валами с параллельными, пересекающимися и перекрещивающимися осями, а также для преобразования вращательного движения в поступательное и наоборот. Зубчатые передачи между параллельными валами осуществляются цилиндрическими колесами с прямыми, косыми и шевронными зубьями (рис. 2.7, а - г). Передачи между валами с пересекающимися осями осуществляются обычно коническими колесами с прямыми и круговыми зубьями (рис. 2.7, е-з), реже тангенциальными зубьями (рис. 2.7, ж). Зубчатые передачи для преобразования вращательного движения в поступательное и наоборот осуществляются цилиндрическим колесом и рейкой (рис. 2.7, д).
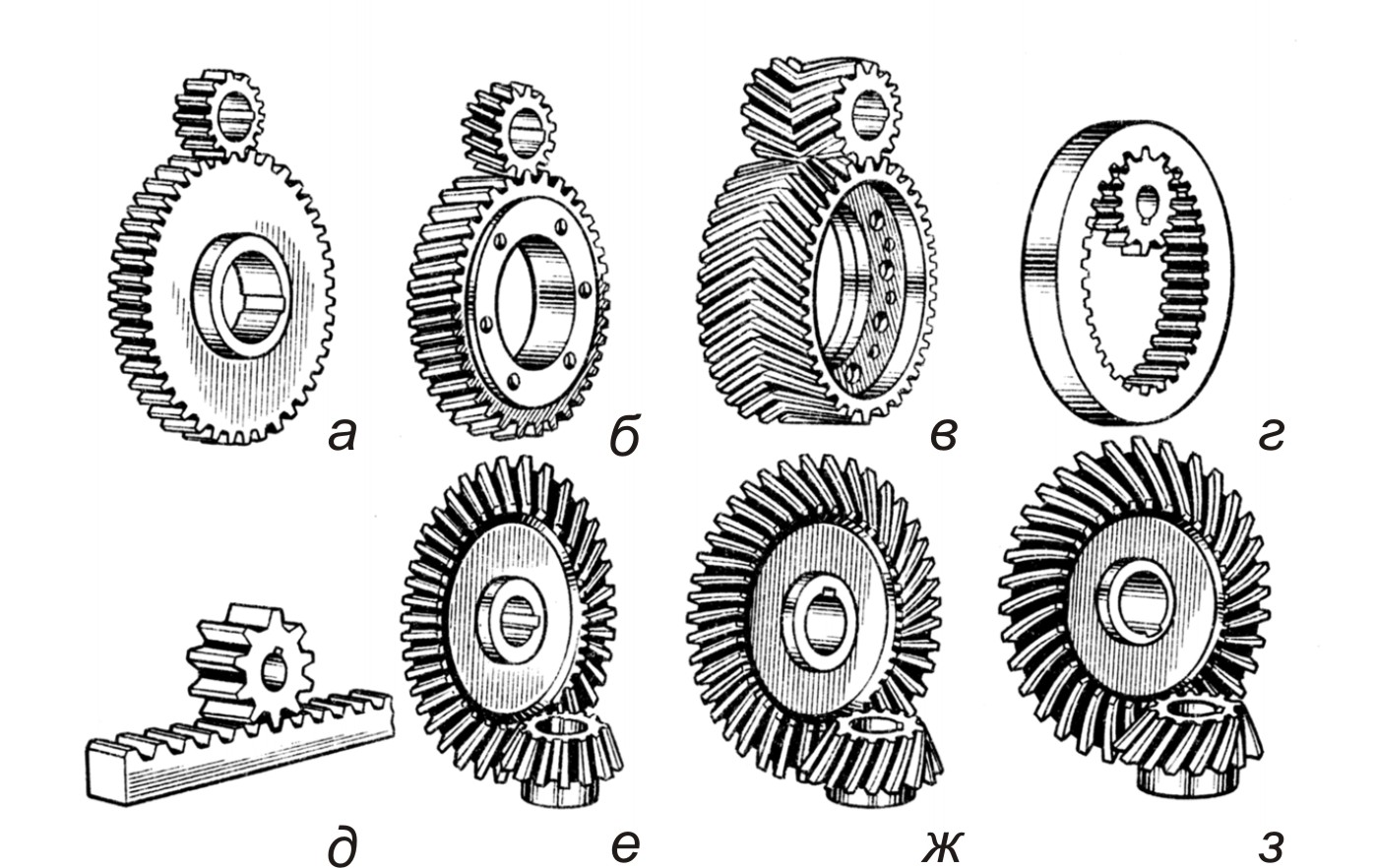
Рис. 2.7. Основные виды зубчатых колес:
а – г – цилиндрические; д – цилиндрическое колесо и рейка;
е – з – конические
Для валов с перекрещивающимися осями применяют зубчато-винтовые передачи.
Зубчатые передачи составляют наиболее распространенную и важную группу механических передач.
Зубчатые передачи в сравнении с другими механическими передачами обладают существенными достоинствами, а именно:
малыми габаритами;
высоким КПД;
большой надежностью в работе;
постоянством передаточного отношения из-за отсутствия проскальзывания;
возможностью применения в широком диапазоне моментов, скоростей и передаточных отношений.
К недостаткам зубчатых передач могут быть отнесены требования высокой точности изготовления и шум при работе со значительными скоростями.
Основные параметры зубчатых передач
Кривые, ограничивающие боковые поверхности зубьев, называют их профилями; два касающихся друг друга профиля называют сопряженными профилями. Оба профиля зуба, как правило, образованы одинаковыми кривыми. Если образующие боковых поверхностей зубьев параллельны оси вращения, то зубья называют прямыми, а передачу прямозубой.
Наиболее распространены передачи с эвольвентным профилем зуба. Такой профиль позволяет зубьям при вращении колес обкатываться друг по другу, отчего зубчатая передача работает плавно, с небольшими потерями энергии на трение.
Меньшее из пары зубчатых колес называют шестерней, а большее – колесом. Термин «зубчатое колесо» является общим. Параметрам шестерни приписывают индекс 1, а параметрам колеса – 2 (рис. 2.8). Кроме того, различают индексы, относящиеся: w – к начальной поверхности или окружности; b – к основной поверхности или окружности; a – к поверхности или окружности вершин и головок зубьев; f – к поверхности или окружности впадин и ножек зубьев. Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.
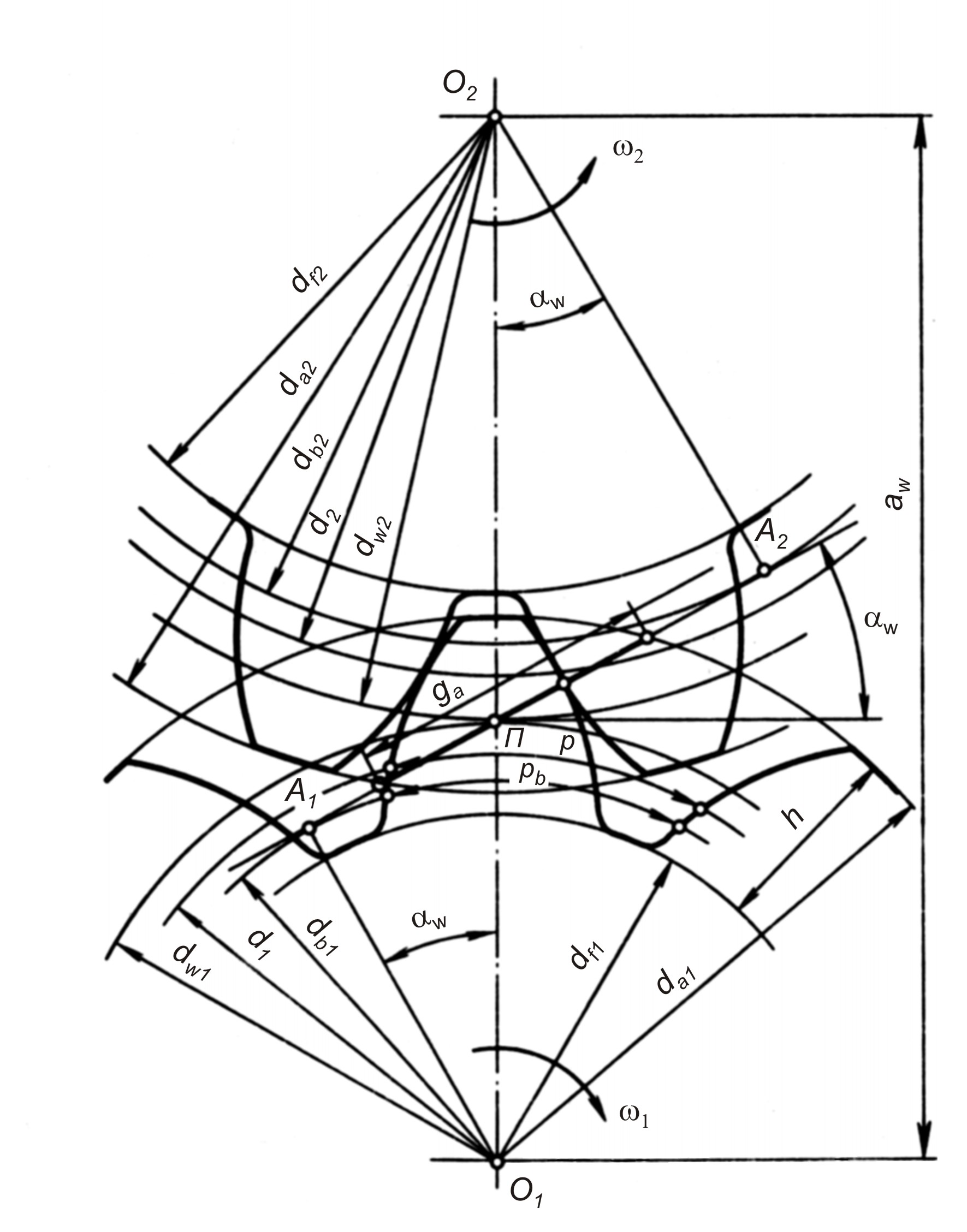
Рис. 2.8. Элементы зубчатого зацепления
Общие понятия о параметрах пары зубчатых колес и их взаимосвязи проще всего уяснить, рассматривая прямозубые колеса.
При вращении зубчатых колес можно представить себе две касающиеся окружности, которые катятся одна по другой без скольжения. Эти окружности с диаметрами d1 и d2 называют начальными. При изготовлении стандартных зубчатых колес начальные окружности используются для настройки зуборезного станка, в этом случае они совпадают с так называемыми делительными окружностями.
Для зубчатой передачи справедливо выражение
.
Однако воспользоваться им для практического определения передаточного числа нельзя, так как d1 и d2 – диаметры воображаемых окружностей. Поэтому передаточное число необходимо выразить через другие, действительно существующие величины.
Зацепление зубчатых колес в передаче требует соблюдения основного условия: зуб одного колеса должен точно входить в соответствующую ему при зацеплении впадину другого колеса. Таким образом, можно сказать, что зубчатое зацепление возможно лишь при равенстве окружных шагов, измеренных по дугам делительных (начальных) окружностей. Шаг – это длина отрезка дуги делительной (начальной) окружности, равная длине всей начальной окружности, разделенной на число зубьев z. (Расстояние t между двумя одноименными (правыми или левыми) профилями соседних зубьев, измеренное по дуге окружности, называют шагом зубчатого колеса.) На одном колесе эта зависимость выразится так:
,
на другом
.
Следовательно,
и отсюда
.
Так как
,
то окончательно
.
Следовательно, передаточное число зубчатой передачи подсчитывается как отношение чисел зубьев ведомого и ведущего колес.
Если через шаг зубчатой
передачи выразить диаметр делительной
окружности, то для первого колеса
для второго
.
В обоих выражениях
есть одна и та же величина
.
Поскольку эта
величина не может быть подсчитана
точно, более удобно вместо нее ввести
величину, называемую модулем
зубчатого колеса:
.
Модуль является основной геометрической характеристикой зубчатого колеса. Величина модуля стандартизована, это облегчает изготовление и подбор зубчатых колес.
Расстояние от делительной окружности до вершины зуба называется головкой зуба, а от делительной окружности до основания зуба – ножкой зуба.
Для цилиндрического колеса можно определить основные размеры:
диаметр делительной окружности
;
диаметр окружности выступов
;
диаметр окружности впадин
.
Расстояние между центрами колес (межосевое расстояние)
.
Модуль колеса легко посчитать, измерив диаметр окружности выступов и разделив его на число зубьев, увеличенное на два (с последующим округлением до ближайшей стандартной величины), т.е.
.
Приведенные выводы справедливы только для зубчатых колес с прямыми зубьями. Геометрический расчет косозубых и шевронных колес более сложен и здесь не приводится.