26.Угол между прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых.
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами s1 и s2. Так как
т
о
по формуле для косинуса угла между
векторами получим:
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов s1 и s2:
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. L1параллельна L2тогда и только тогда, когда s1 параллелен
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:
27 Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией на плоскость. Пусть прямая и плоскость заданы уравнениями
Рассмотрим векторы
и
.
Если угол между ними острый, то он будет
,
где φ – угол между прямой и плоскостью.
Тогда
.
Если угол между векторами
и
тупой,
то он равен
.
Следовательно
.
Поэтому в любом случае
.
Вспомнив формулу вычисления косинуса
угла между векторами, получим
.
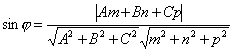Условие перпендикулярности прямой и
плоскости. Прямая и плоскость
перпендикулярны тогда и только тогда,
когда направляющий вектор прямой
и
нормальный вектор
плоскости
коллинеарны, т.е.
.
Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.
28 Условие принадлежности двух прямых одной плоскости
| |
x-x1 |
y-y1 |
z-z1 |
| |
|
| |
l1 |
m1 |
n1 |
| |
= 0 |
| |
l2 |
m2 |
n2 |
| |
|
Если это условие выполняется, прямые или параллельны или пересекаются
29 Цилиндрические поверхности с образующими параллельными одной из координатных осей
Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндрической поверхностью или цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L — его образующей (см. рис. 83).
Б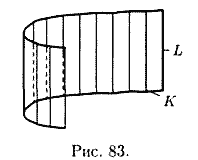
удем
рассматривать цилиндрические поверхности,
направляющие которых лежат в одной из
координатных плоскостей, а образующие
параллельны координатной оси,
перпендикулярной этой плоскости.
Пусть в плоскости Оху лежит некоторая линия К, уравнение которой
.
(12.21)
Построим цилиндр с образующими параллельными оси Oz и направляющей К.
Теорема 12.1. Уравнение цилиндра, образующие которого параллельны оси Oz, имеет вид (12.21), т. е. не содержит координаты z.
В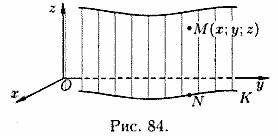
озьмем
на цилиндре любую точку
(см.
рис. 84). Она лежит на какой-то образующей.
Пусть N — точка пересечения этой
образующей с плоскостью Оху. Следовательно,
точка N лежит на кривой K и ее координаты
удовлетворяют уравнению (12.21).
Но точка Μ имеет такие же абсциссу x и ординату у, что и точка N. Следовательно, уравнению (12.21) удовлетворяют и координаты точки , так как оно не содержит z. И так как Μ — это любая точка цилиндра, то уравнение (12.21) и будет уравнением этого цилиндра.
Теперь ясно, что
есть
уравнение цилиндра с образующими,
параллельными оси Оу, a
с
образующими, параллельными оси Ox.
Название цилиндра определяется названием
направляющей. Если направляющей служит
эллипс
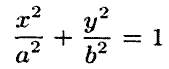
30 Конические поверхности
Поверхность, образованная прямыми линиями, проходящими через данную точку Ρ и пересекающими данную плоскую линию L (не проходящую через Ρ), называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Ρ — ее вершиной, а прямая, описывающая поверхность, называется образующей.
П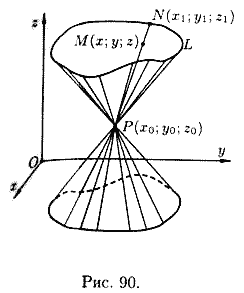
усть
направляющая L задана уравнениями
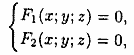(12.24)
а точка
-
вершина конуса. Найдем уравнение конуса.
Возьмем на поверхности конуса произвольную
точку
(см.
рис. 90). Образующая, проходящая через
точки Ρ и М, пересечет направляющую L в
некоторой точке
.
Координаты точки N удовлетворяют
уравнениям (12.24) направляющей:
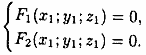(12.25)
Канонические уравнения образующих, проходящих через точки Ρ и Ν, имеют вид
(12.26)
Исключая x1, у1 и z1 из уравнений (12.25) и (12.26), получим уравнение конической поверхности, связывающее текущие координаты х, у и z.
31 Поверхности вращения
Поверхность, образованная вращением
некоторой плоской кривой вокруг оси,
лежащей в ее плоскости, называется
поверхностью вращения. Пусть некоторая
кривая L лежит в плоскости Oyz. Уравнения
этой кривой запишутся в виде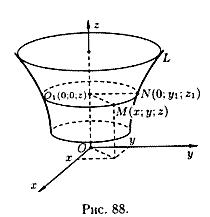
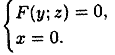(12.22)
Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.
Возьмем на поверхности произвольную
точку
(см.
рис. 88). Проведем через точку M плоскость,
перпендикулярную оси Oz, и обозначим
точки пересечения ее с осью Oz и кривой
L соответственно через O1
и N. Обозначим координаты точки N через
.
Отрезки
и
являются
радиусами одной и той же окружности.
Поэтому
.
Но
,
.
Следовательно,
или
.
Кроме того, очевидно,
.
Так как точка N лежит на кривой L, то ее
координаты удовлетворяют уравнению
(12.22). Стало быть,
.
Исключая вспомогательные координаты
y1 и z1 точки N, приходим к
уравнению
32 Эллипсоид
Исследуем поверхность, заданную уравнением
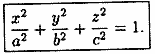(12.28)
Рассмотрим сечения поверхности (12.28) с
плоскостями, параллельными плоскости
хОу. Уравнения таких плоскостей:
,
где h — любое число.
Линия, получаемая в сечении, определяется двумя уравнениями
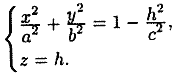(12.29)
Исследуем уравнения (12.29):
а) Если
,
,
то
.
Точек пересечения поверхности (12.28) с
плоскостями
не
существует.
б) Если
,
т. е.
,
то
.
Линия пересечения (12.29) вырождается в
две точки
и
.
Плоскости
и
касаются
данной поверхности.
в) Если
,
то уравнения (12.29) можно переписать в
виде:
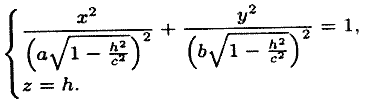
Как видно, линия пересечения есть эллипс с полуосями (см. рис. 91)
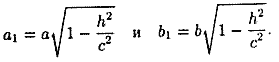
При этом чем меньше
,
тем больше полуоси
и
.
При
они
достигают своих наибольших значений:
,
.
Уравнения (12.29) примут вид
Аналогичные результаты получим, если
рассмотрим сечения поверхности (12.28)
плоскостями
и
.
Таким образом, рассмотренные сечения
позволяют изобразить поверхность
(12.28) как замкнутую овальную поверхность.
Поверхность (12.28) называется эллипсоидом.
Величины а, b и с называются полуосями
эллипсоида. Если все они различны, то
эллипсоид называется трехосным; если
какие-либо две полуоси равны, трехосный
эллипсоид превращается в эллипсоид
вращения; если
,
то — в сферу
.
33 Гиперболоиды
Однополостный гиперболоид
Исследуем поверхность, заданную уравнением
(12.30)
Пересекая поверхность (12.30) плоскостью ι, получим линию пересечения, уравнения которой имеют вид
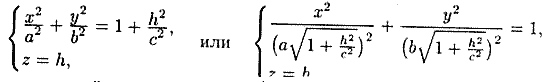
Как видно, этой линией является эллипс с полуосями
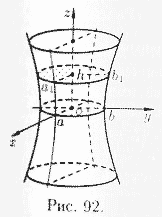
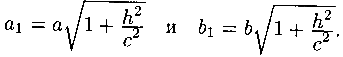
Полуоси и достигают своего наименьшего значения при : , . При возрастании полуоси эллипса будут увеличиваться.
Если пересекать поверхность (12.30) плоскостями или , то в сечении получим гиперболы. Найдем, например, линию пересечения поверхности (12.30) с плоскостью Oyz, уравнение которой x = 0. Эта линия пересечения описывается уравнениями
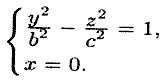
Как видно, эта линия есть гипербола (см. рис. 92).
Анализ этих сечений показывает, что поверхность, определяемая уравнением (12.30), имеет форму бесконечной расширяющейся трубки. Поверхность (12.30) называется однополостным гиперболоидом.
Замечание: можно доказать, что через любую точку гиперболоида (12.30) проходят две прямые, лежащие на нем.
Двухполостный гиперболоид
Пусть поверхность задана уравнением
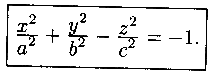(12.31)
Если поверхность (12.31) пересечь плоскостями , то линия пересечения определяется уравнениями
(12.32)
Отсюда следует, что:
а) если , то плоскости не пересекают поверхности;
б) если
,
то плоскости
касаются
данной поверхности соответственно в
точках
и
.
в) если , то уравнения (12.32) могут быть переписаны так
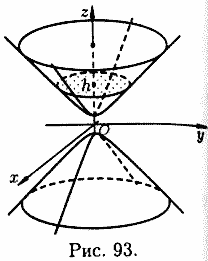
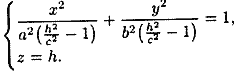
Эти уравнения определяют эллипс, полуоси которого возрастают с ростом .
Пересекая поверхность (12.31) координатными плоскостями Oyz (x=0) и Οxz (у = 0), получим в сечении гиперболы, уравнения которых соответственно имеют вид
У обеих гипербол действительной осью является ось Οz. Метод сечения позволяет изобразить поверхность
(см. рис. 93), определяемую уравнением (12.31), как поверхность, состоящую из двух полостей, имеющих форму выпуклых неограниченных чаш. Поверхность (12.31) называется двухполостным гиперболоидом.
34 Параболоиды
ллиптический параболоид
Исследуем повевхность, заданную уравнением
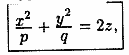
(12.33)
где
,
.
Рассечем поверхность (12.33) плоскостями
.
В сечении получим линию, уравнения
которой есть
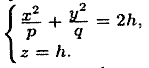
Если
,
то плоскости
поверхности
не пересекают; если
,
то плоскость
касается
поверхносп в точке
;
если
,
то в сечении имеем эллипс, уравнение
которого имеет вид
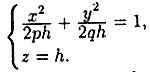
Его полуоси возрастают с ростом h. При
пересечении поверхности (12.33)
координатными плоскостями Oxz и Oyz
получатся соответственно параболы
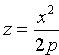и
.
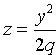Таким образом, поверхность, определяемая
уравнением (12.33), имеет вид выпуклой,
бесконечно расширяющейся чаши (см. рис.
94). Поверхность (12.33) называется
эллиптические параболоидом.
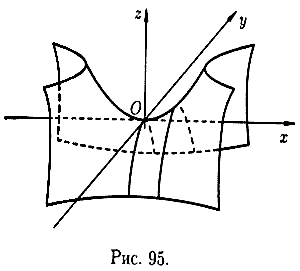
Гиперболический параболоид
Исследуем поверхность, определяемую уравнением
(12.34)
где и . Рассечем поверхность (12.34) плоскостями . Получим кривую
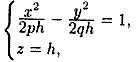
которая при всех значениях
является
гиперболой. При
ее
действительные оси параллельны оси Ox;
при
—
параллельны оси Оу;
при
линия
пересечения
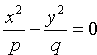распадается
на пару пересекающихся прямых
и
.
При пересечении
поверхности плоскостями, параллельными плоскости Οxz (у = h), будут получаться параболы
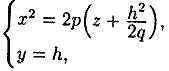
ветви которых направлены вверх. При
в
сечении получается парабола
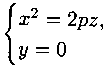
с вершиной в начале координат и осью симметрии Οz.
Пересекая поверхность
(12.34) плоскостями
,
получим параболы
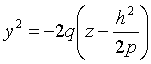ветви
которых направлены вниз.
Анализ линии пересечения позволяет определить вид поверхности: она имеет вид седла (см. рис. 95). Поверхность (12.34) называется гиперболическим параболоидом.
35 Поверхности второго порядка (обзор всех возможных видов)
поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени:
a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 (*)
Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из 17 приведённых ниже канонических видов, каждому из которых соответствует определённый класс П. в. п. Среди них выделяют пять основных типов поверхностей. Именно,
1) эллипсоиды
— эллипсоиды,
— мнимые эллипсоиды;
2) гиперболоиды:
— однополостные гиперболоиды,
— двуполостные гиперболоиды;
3) параболоиды (p > 0, q > 0):
— эллиптические параболоиды,
— гиперболические параболоиды;
4) конусы второго порядка:
— конусы,
— мнимые конусы;
5) цилиндры второго порядка:
— эллиптические цилиндры,
— мнимые эллиптические цилиндры,
— гиперболические цилиндры,
— параболические цилиндры.
Перечисленные П. в. п. относятся к т. н. нераспадающимся П. в. п.; распадающиеся П. в. п.:
— пары пересекающихся плоскостей,
36 Определение линейного векторного пространства (аксиоматическое) Примеры пространств
Пусть V - непустое множество (его
элементы будем называть векторами и
обозначать
...),
в котором установлены правила:
1) любым двум элементам
соответствует
третий элемент
называемый
суммой элементов
(внутренняя
операция);
2) каждому
и
каждому
отвечает
определенный элемент
(внешняя
операция).
Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:
I.
II.
III.
(нулевой
элемент, такой, что
).
IV.
(элемент,
противоположный элементу
),
такой, что
V.
VI.
VII.
VIII.
Аналогично
определяется комплексное линейное
пространство (вместо R рассматривается
C)
37 Простейшие следствия из аксиоматического определения векторного пространства
ХЗ КОТАНЫ ХУЙНЯ КАКАЯ-ТО
38 Понятие подпространства Примеры Понятие линейной оболочки
Предположим, что некоторое подмножество L линейного пространства R удовлетворяет следующим двум требованиям. 1°. Если элементы х и у принадлежат подмножеству L, то и сумма х + у принадлежит этому подмножеству. 2°. Если элемент х принадлежит подмножеству L, а λ — любое вещественное число, то и элемент λх принадлежит подмножеству L. Убедимся в том, что подмножество L, удовлетворяющее требованиям 1° и 2°, само является линейным пространством. Достаточно убедиться в справедливости для элементов подмножества L аксиом 1°-8° из определения линейного пространства. Все указанные аксиомы, кроме аксиом 3° и 4°, заведомо справедливы для элементов подмножества L, поскольку они справедливы для всех элементов пространства R. Остается проверить выполнение аксиом 3° и 4°. Пусть х — любой элемент подмножества L, а λ — любое вещественное число. Тогда в силу требования 2° элемент λх также принадлежит L. Остается заметить, что (в силу теоремы 2.2) этот элемент λх при λ = 0 превращается в нулевой элемент пространства R, а при λ = - 1 превращается в противоположный для х элемент. Таким образом, подмножеству L принадлежит нулевой элемент и противоположный (для каждого элемента х) элемент, а это и означает, что для элементов подмножества L справедливы аксиомы 3° и 4°. Тем самым полностью доказано, что подмножество L само является линейным пространством. Определение. Подмножество L линейного пространства R, удовлетворяющее требованиям 1° и 2°, называется линейным подпространством (или просто подпространством) пространства R. Простейшими примерами подпространств могут служить: 1) так называемое нулевое подпространство, т.е. подмножество линейного пространства R, состоящее из одного нулевого элемента; 2) все пространство R (которое, конечно, можно рассматривать как подпространство).
39 Линейная зависимость (определение, критерий линейной зависимости, примеры, понятие ранга системы векторов)
http://www.cleverstudents.ru/linear_dependence.html
40 Определение конечномерною пространства Понятие базиса в конечномерном пространстве Теорема о существовании базиса (с доказательством)
Говорят,
что пространство
конечномерно3),
если
или
базис
состоит
из конечного числа векторов. В противном
случае говорят, что бесконечномерно
41 Координаты вектора в данном базисе
Любой
вектор
плоскости
единственным образом выражается в
виде:
,
где
–
числа, которые называются координатами
вектора в данном базисе. А само
выражение
называется
разложением вектора
по
базису
42 Координаты вектора в базисе и их изменение при переходе к другому базису
Пусть
— 
-мерное
векторное пространство над полем 
с
некоторыми базисами 
и 
.
Векторы одного базиса можно выразить через векторы другого:
.
Определение 4. Матрица, определенная коэффициентами вышеприведенного разложения
,
называется матрицей перехода от базиса к базису .
Замечание
1. Координаты
вектора 
относительно
базиса
образуют 
-й столбец матрицы 
.
Предложение
3. Пусть
вектор 
имеет
координаты 
в
базисе
и
координаты 
в
базисе
.
При переходе от базиса
к
базису
координаты
вектора
в
новом базисе выражаются через координаты
в старом базисе по формуле:
,
где 
—
матрица, обратная к
.
43 Теорема о размерности ненулевого подпространства Два способа задания линейного полпространства
44 Линейное преобразование пространства Определение Примеры (не менее четырех) Простейшие свойства линейного преобразования пространства