10 Гипербола (определение, координаты фокусов, расстояния от точки до фокусов)

Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквами   и  , расстояние между ними - через 2с. По определению гиперболы  , или  .

Пусть дана гипербола. Если оси декатовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид

 (1)

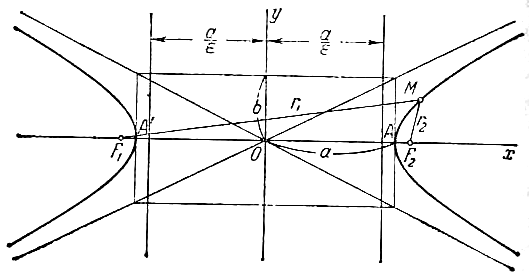г де  . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.

Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.

Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть

, 

Уравнение

 (2)

определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.

Две гиперболы, которые определяются уравнениями

, 

в одной и той же системе координат, называются сопряженными.

Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид

 или 

Число

где а - расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы  . Если М(x; y) - произвольная точка гиперболы, то отрезки   и   (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам

,  ,

фокальные радиусы точек левой ветви - по формулам

,  .

Если гипербола задана уравнением (1), то прямые, определяемые уравнениями

,  ,

называются ее директрисами (см. рис.). Если гипербола задана уравнением (2), то директрисы определяются уравнениями

,  .

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:

.

11 Исследование формы гиперболы по ее каноническому уравнению

Рассмотрим гиперболу, заданную в некоторой прямоугольной декартовой системе координат своим каноническим уравнением

        (1)

Отметим следующие свойства гиперболы:

1) Гипербола (1) не имеет общих точек с осью Оу, a ось Ох пересекает в двух точках.

Для определения координат точек пересечения гиперболы (1) с осью Оу нужно решить совместно их уравнения

,     x = 0

Подставляя x = 0 в уравнение гиперболы, получим y² = — b², а это означает, что система не имеет решений. Следовательно, гипербола не пересекает ось ординат.

Для определения координат точек пересечения гиперболы (1) с осью Ох нужно решить совместно их уравнения

,     y = 0

Точка пересечения гиперболы с осью Ох должна иметь ординату у = 0 и в то же время принадлежать гиперболе. Подставив у = 0  в уравнение гиперболы, получим

х = ± а .

Итак, точками пересечения гиперболы (1) с осью Ох будут точки А(а; 0) и В(—а; 0); они называются вершинами гиперболы.

Отрезок АВ называется действительной осью гиперболы. Длина отрезка АВ, очевидно, равна 2а. Число а называют действительной полуосью гиперболы, число b - мнимой полуосью.

2) Гипербола имеет две взаимно перпендикулярные оси симметрии.

В уравнение (1) переменные х и у входят только во второй степени. Следовательно, если координаты точки N(х; у) удовлетворяют уравнению (1), то этому же уравнению будут удовлетворять и координаты точек N₁(—х; у) и N₂(x; —у).

Легко видеть, что точка N₁ симметрична точке N относительно оси ординат, точка N₂ симметрична точке N относительно оси абсцисс.

Таким образом, гипербола имеет две оси симметрии, oни взаимно перпендикулярны.

3) Гипербола имеет центр симметрии.

Если координаты точки N(x; у) удовлетворяют уравнению (1), то этому же уравнению удовлетворяют и координаты точки К(—х; —у). Точка К, очевидно,симметрична точке N относительно начала координат. Таким образом, гипербола имеет центр симметрии. Центр симметрии гиперболы называется центром гиперболы.

4) Гипербола (1) пересекается с прямой у = kx при | k |< ^b/_a в двух точках.  Если | k |> ^b/_a    , то общих точек у гиперболы и прямой нет.

Для определения координат точек пересечения гиперболы (1) и прямой у = kx нужно решить систему уравнений

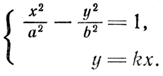           (2)

Исключая у, получаем

откуда

(b² — k²a²)x² = a²b².

При b² — k²a² < 0, т. е. при | k |> ^b/_a ,   полученное уравнение, а поэтому и система (2) решений не имеют. Следовательно, прямые, проходящие через начало координат с угловым коэффициентом, модуль которого больше или равен    ^b/_a   не пересекают гиперболу (1).   Прямые с уравнениями у = ^b/_a х и у = — ^b/_a х называютсяасимптотами гиперболы (1).

При b² — k²a² > 0, т. е. при | k |< ^b/_a система (2) имеет два решения:

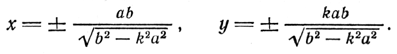
С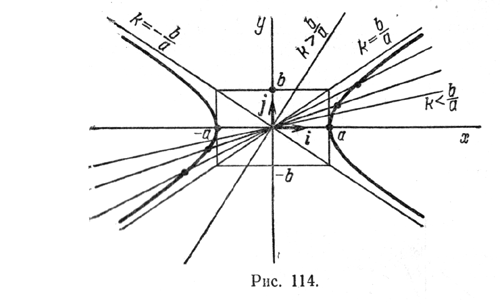 ледовательно, каждая прямая, проходящая через начало координат с угловым коэффициентом, модуль которого меньше    ^b/_a  пересекает гиперболу (1) в двух точках  (рис. 114).

При k = 0 из формул (3) получаем х = ±а, у = 0, т. е. прямая у = 0 пересекает гиперболу в ее вершинах.

Так как гипербола симметрична относительно осей координат, то достаточно изучить ее форму в первом квадранте координатной плоскости. Из формул

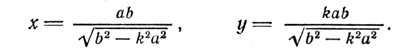         k > 0

видно, что при возрастании й от нуля до ^b/_a  (при этом прямая у = kx поворачивается против движения часовой стрелки) и абсциссы и ординаты точек пересечения прямой с гиперболой возрастают. Прямая у = kx пересекaет гиперболу во все более далеких от начала координaт точках. Таким образом, гипербола (1) имеет вид, изображенный на рис. 114. Она состоит из двух не связанных между собой частей, называемых ее ветвями