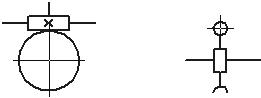8 Структурный синтез рычажных механизмов

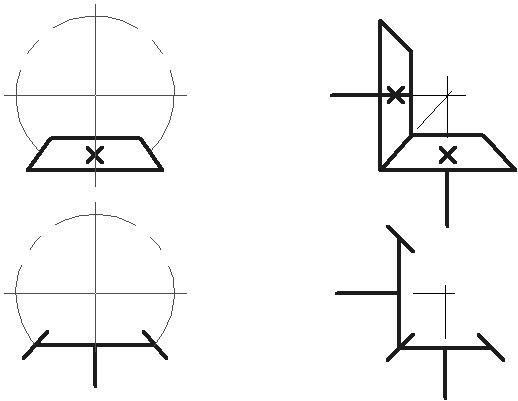
Задача структурного синтеза механизмов является обратной по отношению к задаче структурного анализа и состоит в проектировании структурной схемы механизма. Синтез механизмов возможен двумя методами. Первый метод заключается в присоединении к основному механизму одной или нескольких групп Ассура. При этом следует иметь в виду, что добавление к механизму структурной группы любого класса и вида не должно менять степени подвижности механизма. На рис. 11 приведены примеры образования механизмов II класса (рис. 11, а) и III класса (рис. 11, б).

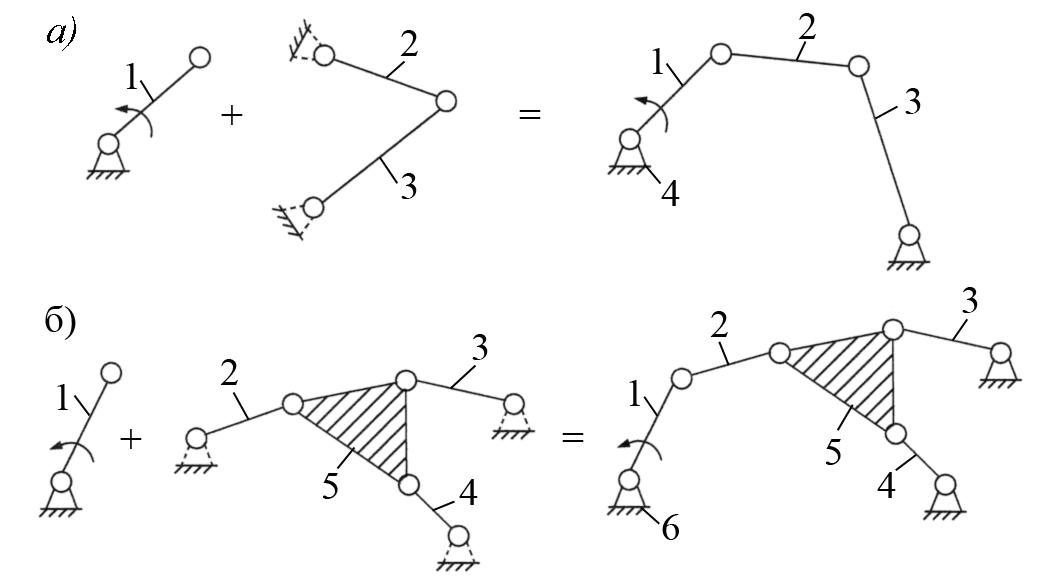
Рис. 11

Второй метод синтеза состоит в преобразовании одного из звеньев структурной группы в два звена, образующих поступательную кинематическую пару V или IV классов. На рис. 12, а, б представлены структурные группы и гидрорычажные механизмы соответственно II и IV классов, образованные этим методом.

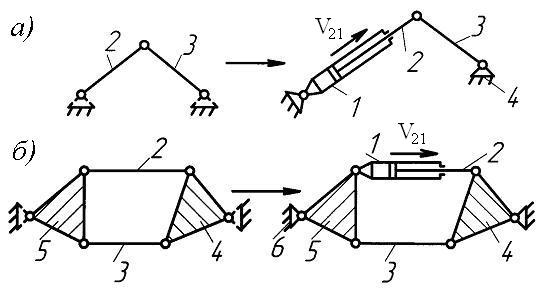
Рис. 12

Следует отметить, что для механизмов с гидроприводом заданным является относительное движение поршня 2 в цилиндре 1, поэтому их структурный анализ по Ассуру не возможен. Механизм должен рассматриваться как неделимая структурная единица – гидрорычажный механизм соответствующего класса.

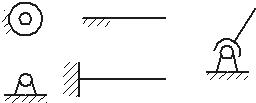
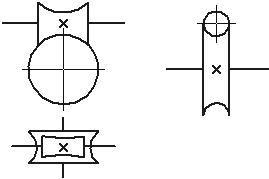
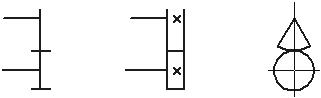
Условные обозначения кинематических пар и звеньев.

Таблица

Вал, валик, ось, стержень, шатун и т.п
Неподвижное звено (стойка). Для указания неподвижности любого звена часть его контура покрывают штриховкой
Неподвижное соединение частей звена
Неподвижное соединение частей звена, допускающее регулировку
Неподвижное соединение детали с валом, стержнем
Вращательная кинематическая пара
Вращательная многократная (двухкратная) кинематическая пара
Поступательная кинематическая пара
Винтовая кинематическая пара
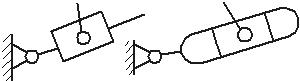
Цилиндрическая кинематическая пара
Кинематическая пара сферическая с пальцем
Кинематическая пара карданного шарнира
Сферическая кинематическая пара
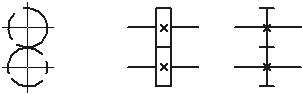
Подшипники скольжения радиальные
Кулачки плоские
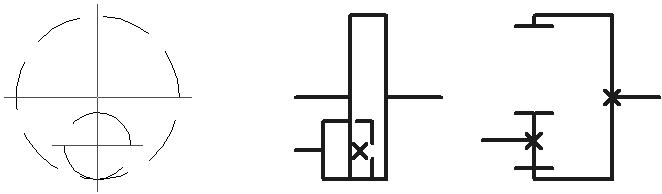
Кулачки вращающиеся
Толкатель дуговой
Толкатель роликовый
Толкатель плоский
Ползун
Кулиса
Звено рычажных механизмов трёхэлементное
Цилиндрические зубчатые передачи внешнего зацепления
Цилиндрические зубчатые передачи внутреннего зацепления
Цилиндрические зубчатые передачи с некруглыми колёсами
Передачи с пересекающимися валами
Передачи зубчатые со скрещивающимися валами гипоидные
Передачи зубчатые со скрещивающимися валами червячные
Передачи зубчатые со скрещивающимися валами глобоидные
Передачи зубчатые реечные
Передачи зубчатые сектором
Винт, передающий движение
Гайка на винте

Порядок проведения лабораторной работы

1. Изучить основные понятия и определения, условные обозначения кинематических пар и звеньев.

2. Составить структурные схемы четырёх плоских механизмов, данных преподавателем: по две схемы рычажных и зубчатых механизмов.

3. Провести структурный анализ плоских рычажных механизмов: определить по формуле Чебышева количество избыточных связей q. Если в механизме имеется контурная избыточная связь (q=1), необходимо сделать механизм оптимальным, удалив звено, которое вносит избыточную связь.

4. Изобразить структурную схему полученного оптимального механизма и убедиться с помощью формулы Чебышева, что механизм действительно не имеет избыточных связей (q=0).

5. Оптимальные рычажные механизмы (q=0) без высших кинематических пар (р_в=0), рассчитанные в пунктах 3 и 4, необходимо представить в виде совокупности одной или нескольких структурных групп и одного (при W=1) или нескольких (при W>1) начальных механизмов. При этом следует различать, чем является совокупность четырёх звеньев и шести кинематических пар – группами III-IV классов или соединением двух простейших структурных групп II класса.

6. Для заданных зубчатых механизмов проверить наличие или отсутствие в них избыточных связей q.

7. Два оптимальных рычажных механизма (рассмотренных в пунктах 3 и 4) представить в виде пространственных, т.е. реально изготовленных механизмов. Определить количество избыточных связей по формуле Малышева. Преобразовать эти механизмы путём понижения класса кинематических пар

1) в оптимальные механизмы;

2) в механизмы с дополнительной степенью подвижности (q<0) – местной или групповой.

Контрольные вопросы.

1. Определение механизма, звена, кинематической пары.

2. Виды звеньев.

3. Классификация кинематических пар.

4. Определение структурной группы, виды структурных групп.

5. Формула Чебышева с пояснением параметров и коэффициентов, входящих в формулу.

6. Формула Малышева с пояснением параметров и коэффициентов, входящих в формулу.

7. Оптимальные механизмы, механизмы с избыточными связями и дополнительными степенями подвижности.

8. Методы получения оптимальных механизмов – плоских и пространственных.

9. Структурный анализ механизмов.

10.Структурный синтез рычажных механизмов.

Список использованных источников

1. Фролов К.В. и др. Теория механизмов и машин: учеб. Для втузов.- М. : Высшая школа, 2001. 496с.

2. Решетов Л.Н. Самоустанавливающиеся механизмы: Справочник. М., 1979, 334 с.

3. ГОСТ 2.770-68. Обозначения условные графические в схемах. Элементы кинематики.