7.4. Распределение потенциала и концентрации снз в равновесном электрическом переходе

 

Выделим мысленно бесконечно тонкий слой dx электронного газа, заключенный между плоскостями I и II с координатами х и x+dx. Этот слой будет испытывать со стороны окружающего электронного газа давление Р₁ слева и Р₂ справа. Давление газа, как известно, равно nkT, где n- концентрация частиц этого газа. Обозначим концентрацию электронов в плоскости 1 через n₁ а в плоскости II  через n₂. Тогда разность давлений ∆Р на рассматриваемый слой будет равна:

 

                                            (7.1)      

 

Сила перепада давлений, действующая на слой dx, будет равна:

 

                                                                                  (7.2)

 

где s- площадь границ слоя. Знак " - " показывает, что эта сила противоположна направлению вектора градиента концентрации электронов.

          Определим силу электрического поля, действующую на тот же слой. Электрический заряд слоя ∆Q равен:

 

                                                                                           (7.3)

 

Электрическая сила , действующая на слой, будет равна:

 

                                                                                         (7.4)

 

В состоянии равновесия сумма сил, действующих на слой, равна нулю. Следовательно:

 

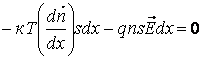
или

                                                                                      (7.5)

 

Так как , то

                                                                                                 (7.6)

 

Решая это дифференциальное уравнение, получим:

 

                                                                                          (7.7)

 

Рассуждая аналогично в отношении дырочного газа, найдем, что

 

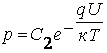                                                                                        (7.8)

 

Константы интегрирования С1 и С2 определяются как всегда из граничных условий. Начало координат мы поместили в глубине однородной области I полупроводника. Здесь выполняется условие локальной электрической нейтральности и поле отсутствует. Примем потенциал этой области в окрестности начала координат равным нулю. Тогда, подставляя в (7.7) и (7.8) значения x = 0; U = 0; n = n₁; p = p₁, получим С1= n₁, С2 = р₁. Следовательно:

                                                                                          (7.9)

                                                                                    (7.10)

          Таким образом, концентрация СНЗ и потенциал в электрическом переходе связаны между собой экспоненциальной зависимостью.

          Распределение потенциала в переходе определим, решив уравнение Пуассона. Плотность пространственного заряда в любом слое равна:

 

                                                                      (7.11)

 

или, учитывая (7.9) и (7.10):

 

                                              (7.12)

 

Следовательно, уравнение  Пуассона будет иметь вид:

 

                                         (7.13)

 

 Поскольку распределение примесей, т.е. (N_d-N_a) = ƒ(х) известно, то, решая (7.13), найдем U = U(x).

          Так как соотношения (7.9) и (7.10) должны быть справедливы для любого элемента объема полупроводника, то, применяя их для второй однородной области, где концентрации электронов и дырок соответственно равны n₂ и p₂ получим, что потенциал этой области U₂ равен:

 

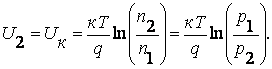                                                     (7.14)

 

Разность потенциалов на концах электрического перехода пропорциональна логарифму отношения концентраций однотипных СНЗ в однородных областях полупроводника, разделенных переходом. Эта разность называется контактной разностью потенциалов перехода.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                  

 

 

 

 

 

 

 

 

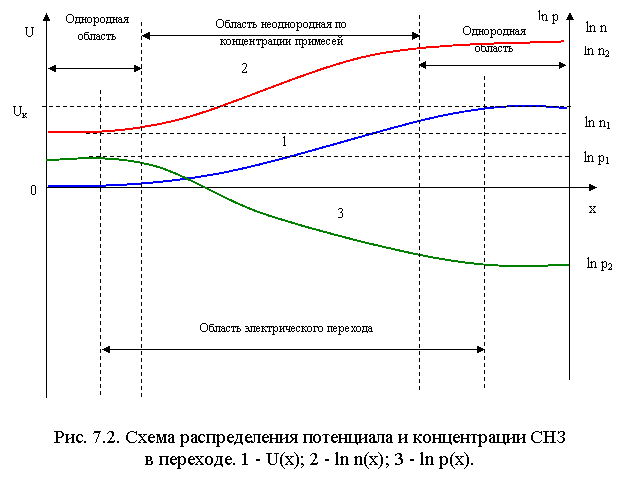
Подводя итог, можно заключить, что в области электрического перехода потенциал возрастает в направлении возрастания разности между концентрацией акцепторных атомов. Соответственно в том же направлении в экспоненциальной зависимости от U возрастает концентрация электронов, а концентрация дырок уменьшается обратно пропорционально концентрации электронов (рис.7.2.)

Ширина электрического перехода всегда превышает ширину области в полупроводнике с неоднородной концентрацией примесей так, что переход частично захватывает области однородного полупроводника.Если ширина неоднородной, по концентрации примесий, области настолько велика, что ее можно считать сравнимой с шириной перехода, то переход называют плавным. Если ширина локализации неоднородности существенно меньше ширины перехода, то переход называют резким.