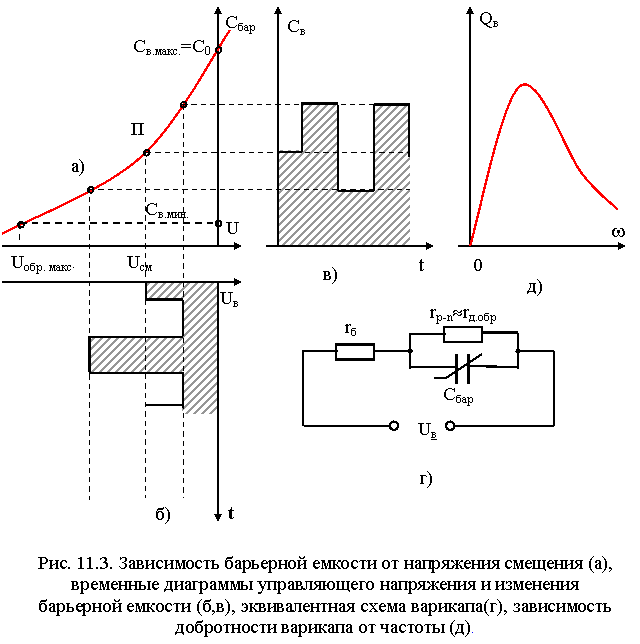
11.3. Варикапы.

 

Полупроводниковый диод, в котором используется зависимость емкости от величины обратного напряжения, и, который предназначен для применения в качестве электрически управляемой емкости, называется варикапом. Помимо систем автоматического управления частоты (АРЧ) гетеродинов, варикапы применяются в качестве умножителей частоты (варакторы) и параметрических усилителей в СВЧ диапазоне (параметрические диоды).

В общем случае зависимость емкости варикапа от величины обратного напряжения может быть представлена выражением:

 

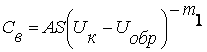                                                                 (11.2)

в котором А - константа, определяемая значением удельной емкости равновесного p-n перехода и значением контактной разности потенциалов U_к. Значение показателя степени m1 зависит от характера распределения примесей в переходе. Для резкого перехода m1=1/2. Величины А и m1, при необходимости, могут быть определены по значению номинальной емкости (при заданном номинальном значении обратного напряжения) и значению так называемого коэффициента перекрытия по емкости К_с. Коэффициент перекрытия по емкости равен отношению емкостей варикапа при двух заданных значениях обратного напряжения.

          Следующим важным параметром варикапа является температурный коэффициент емкости (ТКЕ) _св, характеризующий зависимость С_В от температуры. Эта зависимость обусловлена температурной зависимостью контактной разности потенциалов U_к. ТКЕ равен отношению относительного изменения емкости варикапа к вызывающему его изменению температуры.

          Качество варикапа характеризуется его добротностью Q_В. Добротность варикапа - есть отношение реактивного сопротивления варикапа на заданной частоте переменного напряжения к сопротивлению потерь при заданном значении емкости или постоянного обратного напряжения.

          Полное сопротивление варикапа равно:

 

                                                       

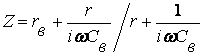
где  r - результирующее сопротивление  параллельно соединенных сопротивлений утечки r_у и дифференциального сопротивления  r_диф. Разделяя активную и реактивную компоненты, получим:

                  

                                                      (11.3)

 

          Отсюда, учитывая, что , найдем

 

                                                                               (11.4)

         

Найденная зависимость добротности от частоты приведена на рис. 11.3        (д).    В области низких частот Св<<1/(rr_б)^1/2, и

 

                                                                                 (11.5)

 

В области высоких частот, напротив Св >> 1/(rr_б)^1/2          и

                                                                                         (11.6)

 

Приравнивая нулю производную Q_В (11.4) по частоте, найдем, что на частоте

 

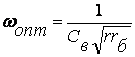                                                                                        (11.7)

 

добротность варикапа максимальна и равна:

 

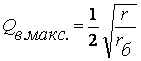                                                                                     (11.8)

 

Отношение r_диф /r_б порядка 10⁷. Отношение r/r_б, из-за наличия сопротивления утечки r_у, несколько меньше. Однако, несмотря на это, добротность варикапов может достигать нескольких тысяч единиц.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таким образом, повышение добротности на низких частотах, как и повышение добротности на оптимальной частоте, требует увеличения дифференциального сопротивления обратно смещенного p-n перехода. Рассмотрим как это может быть реализовано.

Дифференциальное сопротивление r_диф определяется по формуле:

 

                                            (11.9)

 

 

Зависимость ширины перехода Δ от величины приложенного обратного напряжения в случае резкого перехода определяется выражением:

 

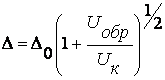                                                                                   (11.10)

 

Где Δ₀ - ширина невозмущенного (равновесного) перехода. В общем случае, охватывающем плавные переходы, указанную зависимость можно представить в виде:

 

                           (11.11)

 

Где m2 ≥ 2. Отсюда

 

 

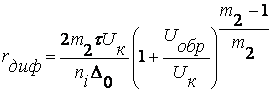                                                       (11.12)

 

 

Если U_{обр.мин.}>>U_к, то

 

 

 

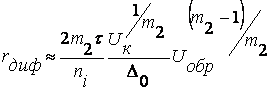                                                  (11.13)

 

 

Таким образом, требуемое увеличение дифференциального сопротивления может быть получено путем использования полупроводника с широкой запрещенной зоной (малое значение n_i) и сравнительно узких p-n переходов.

          На высоких частотах требуемое значение добротности может быть получено путем снижения сопротивления базы. Это достигается либо повышением степени легирования базы, либо применением структур типа      p⁺-n-n⁺. Слой слабо легированного  полупроводника n-типа заключен между сильно легированными слоями p⁺ и n⁺ типов. Слой n-типа берется малой ширины, так что уже при сравнительно небольших обратных напряжениях граница p-n перехода х_n достигает границы n⁺- области. База оказывается расположенной в весьма низкоомной n⁺- области. Достоинством этого метода является то, что наряду с обеспечением малого сопротивления базы, сохраняется большая величина максимально допустимого обратного напряжения. Кроме того, в таких структурах существенно возрастает степень нелинейности зависимости барьерной емкости от обратного напряжения, что очень важно для варакторов, т.е. варикапов, используемых для умножения частоты сигнала.