5 Задача сдэс

Дано: порождающая матрица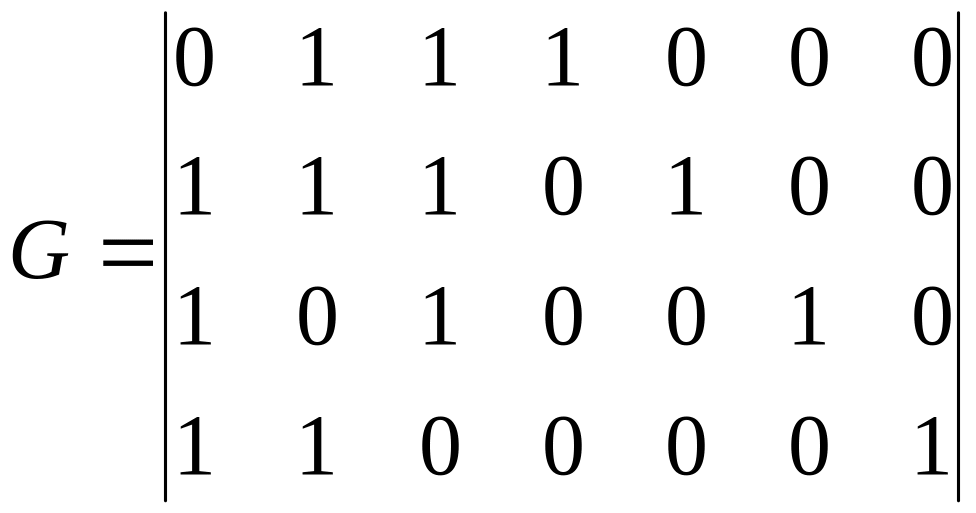

Найти: проверочную матрицу , декодировать кодовое слово 1100011, закодировать последовательность 1111, найти , , .

Решение:

Производящая матрица G состоит из двух матриц: единичной и матрицы , где - число информационных символов, - число проверочных символов, - длина кодовой комбинации.

Элементы, соответствующие 4, 5, 6, 7 столбцам, будут являться информационными, а 1,2,3 – проверочными.

, , - уравнения проверки на четность, они используются для построения проверочной матрицы.

G = .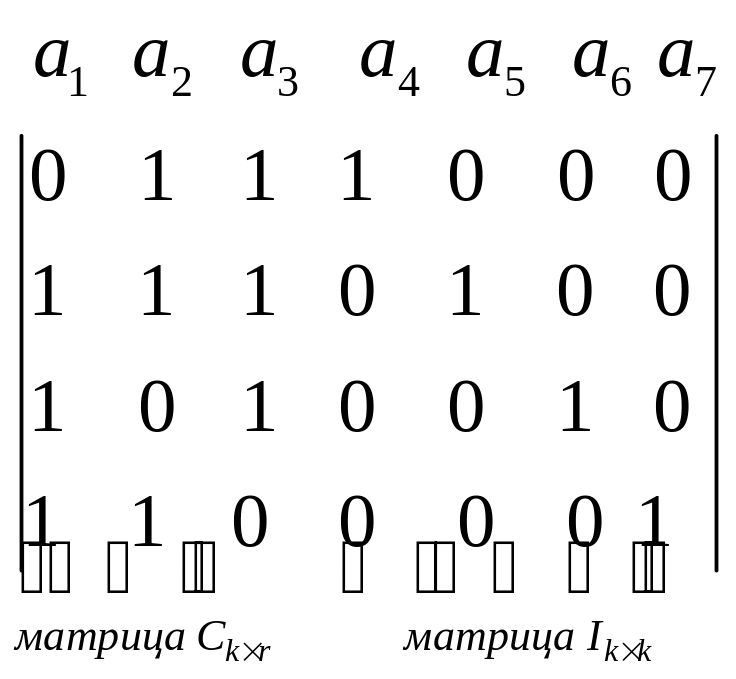

Проверочная матрица состоит из транспонированной матрицы и единичной матрицы . Таким образом число строк равно , а столбцов - .

H = .

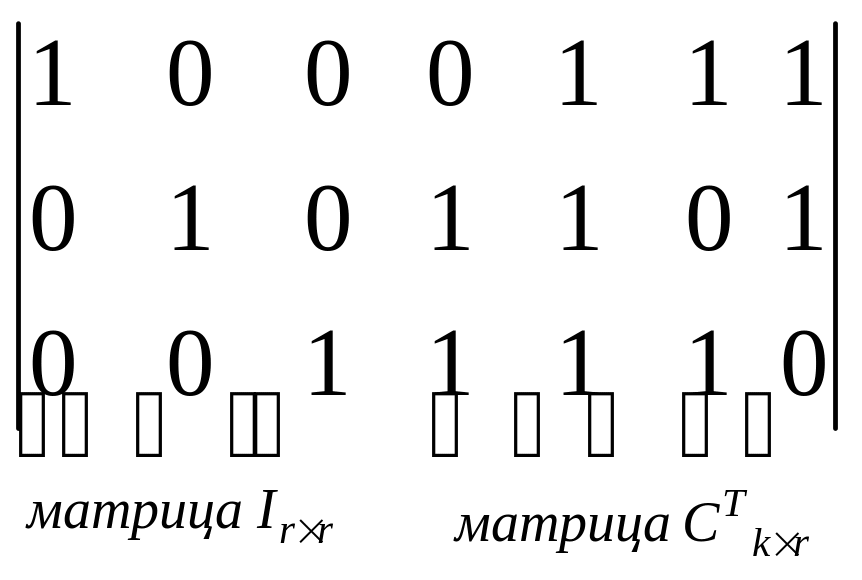Матрица H непосредственно применяется для построения кодирующего устройства:

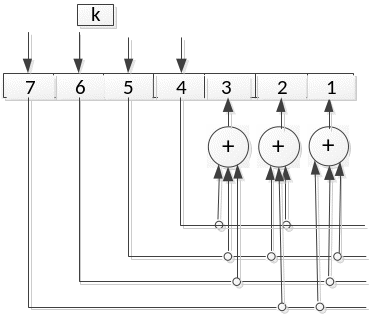
Таким образом, кодовым словом для информационной последовательности 1111 будет 1111111. Или кодирование также можно осуществить умножением информационной последовательности длины на порождающую матрицу G.

Уравнения , , используются для построения декодирующего устройства, которое позволяет обнаружить ошибки. Декодирование также можно осуществить умножением принятой кодовой комбинации на транспонированную матрицу H.

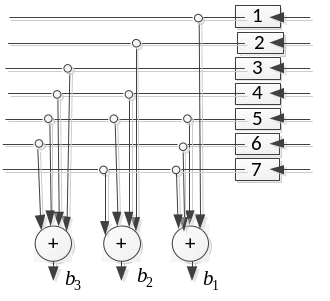
Полученная последовательность - синдром ошибки. Если все равны нулю, кодовая комбинация ошибок не содержит. Если синдром ошибки не равен нулю, значит произошла ошибка. Позицию, в которой произошла ошибка, можно определить по таблице синдромов, которая является транспонированной матрицей H. Данный код позволяет исправить одну ошибку. Если ошибок две, то синдромы складываются. Поэтому нельзя определить, одна ошибка произошла или две.

Таблица синдромов:

Если декодировать слово 1100011получится синдром ошибки 101.

(умножаем, а потом складываем по модулю 2). Следовательно, ошибка произошла в 6 символе кодовой комбинации, а исходная информационная последовательность – 0001 (последние 4 бита кодового слова).

Исходная комбинация – 1100001.

Ак=1111, нумеруем столбики с 4 по 7. Делаем по матрице G.

, ,

Скорость передачи , .

Минимальное кодовое расстояние (не может быть меньше 3).

Число обнаруживаемых и исправляемых ошибок:

, если четное и , если нечетное.

, .

6 Задача сдэс

Дано: , .

Найти: Построить код Рида-Соломона над полем Галуа GF( ), , .

Решение: Код Рида-Соломона – недвоичный линейный циклический блочный код. Является подмножеством кода БЧХ.

Порождающий многочлен в коде Рида-Соломона, исправляющем ошибок, записывается в виде: , где - элементы поля Галуа.

Для построения поля используется неприводимый многочлен . В общем виде поле Галуа GF(2^m) состоит из элементов :

,

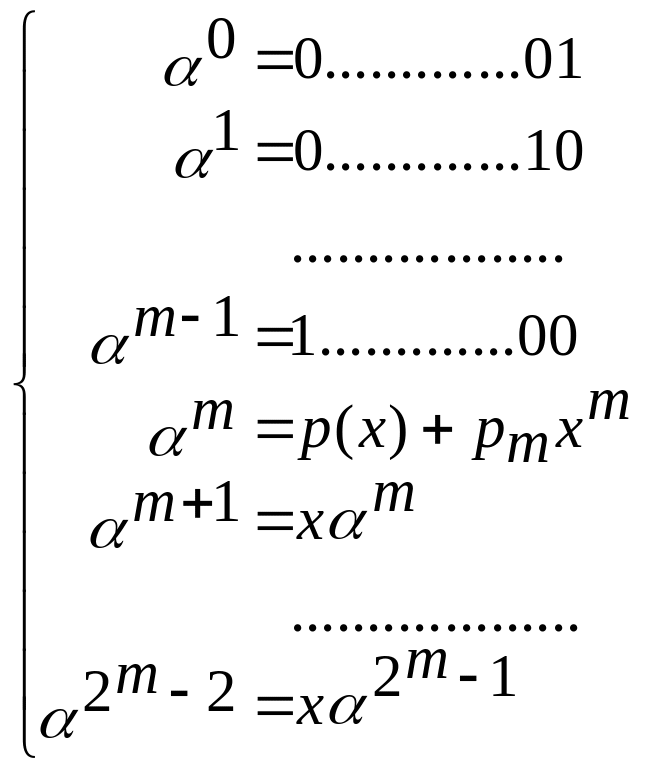То есть элементы до записываются в виде единичной матрицы, а остальные элементы надо вычислять.

Для поля GF( ) неприводимый многочлен: .

,

,

( заменяется на )

Тогда порождающий многочлен кода Рида-Соломона:

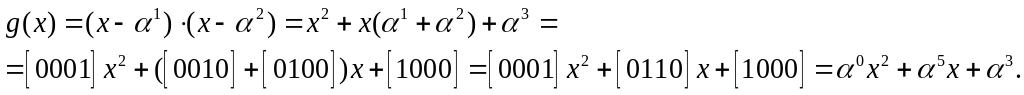
Так как поле GF( ), .

Длина кода =15.

Количество проверочных символов равно наибольшей степени порождающего полинома , т.е. .

Количество информационных символов .

Кодовое расстояние равно числу ненулевых элементов в , т.е. .

Число обнаруживаемых ошибок , . Скорость передачи , .

Избыточность кода , .