1 Задача сдэс

Дано: для кода Хэмминга и m=4, t_{испр.ош}=3 для кода БЧХ.

Найти: Построить коды Хэмминга и БЧХ, сравнить по помехоустойчивости, по , по сложности построения кодирующих и декодирующих устройств.

Решение:

Код Хэмминга:

Параметры кода Хэмминга при проверочных символах:

Длина слова , ,

длина информационной части: , ,

минимальное кодовое расстояние для простого кода Хэмминга .

Код Хэмминга строится на основе проверочной матрицы H r x n.

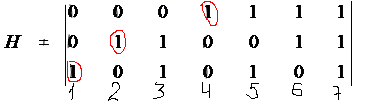
3,5,6,7 – информ; 1,2,4- проверочн.

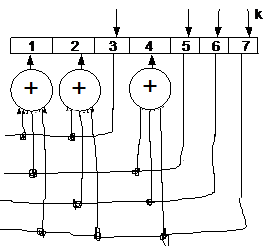
Кодирующее устройство (рисовать не обязательно)

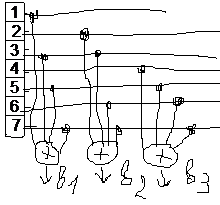
Декодирующее устройство (рисовать не обязательно)

Код БЧХ:

Длина слова , .

,

Неприводимым многочленом для поля GF( ).Так как m0=1,tиспр =3, f min= m0+2tиспр-1=6, i= 1,6

g(х)= (x⁴+x+1)*(x⁴+x³+x²+x+1)*(x²+x+1)=(x⁸+x⁷+x⁶+x⁴+1)*(x²+x+1)=x¹⁰+x⁸+x⁵+x⁴+x²+x+1.

Длина проверочной части равна максимальной степени порождающего полинома r=10.

Длина информационной части k=n-r=15-10=5.

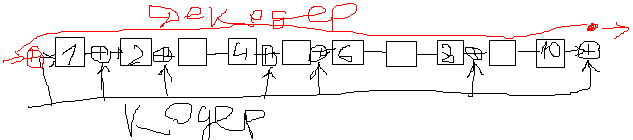
Сравнение:

Для кода БЧХ равно числу ненулевых элементов в :d^*=7.

T_испр= d*-1/2=7-1/2=3 для БЧХ

для Хэмминга

Для кода Хэмминга

Для БЧХ t_обн= 7-1=6

Избыточность .

Для Хэмминга , следовательно

Для БЧХ

Скорость передачи: . Для Хэмминга R=4/7, а для БЧХ R=5/15=1/3

	помехоустойчивость				R	Кодер (Эл-ты задержки и суматоры)		Декодер (Эл-ты задержки и суматоры)
Хэмминга	0,267	3	1	2	4/7	7	3	7	3
БЧХ	0,533	7	3	6	1/3	10	6	10	6

Вывод: БЧХ имеет проще реализацию из-за одинаковой помехоустойчивости

2 Задача сдэс

Дано: .

Найти: закодировать символы ансамбля кодами Шеннона-Фано и Хаффмена, сравнить по коэффициентам относительной эффективности и статистического сжатия.

Решение:

Шеннона-Фано: Алгоритм:

Все имеющиеся букв располагаются в один столбик в порядке убывания вероятностей. Затем эти буквы разбиваются на 2 группы: верхнюю и нижнюю так, чтобы суммарные вероятности этих групп по возможности были ближе друг к другу. Для букв верхней группы в качестве первого символа используется «1», а для нижней – «0». Далее в каждой и выделенных двух групп проводят аналогичные операции.

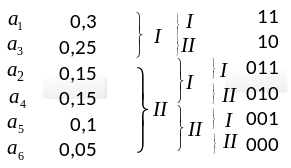
Хаффмана: Алгоритм:

Буквы в алфавите располагаем в порядке убывания вероятностей. Два самых маловероятных сообщения объединяем в одно сообщение, которое имеет вероятность, равную сумме вероятности объединенных сообщений. Снова выбираем два сообщения, имеющие наименьшие вероятности и объединяем их. Повторяем процедуру до тех пор, пока не получим сообщение, вероятность которого равна единице.

Проводя линии, объединяющие сообщения, получаем дерево, в котором отдельные сообщения являются концевыми узлами. Ветвям, которым соответствует меньшая вероятность, присваиваем «0», а ветвям, которым большая – «1».

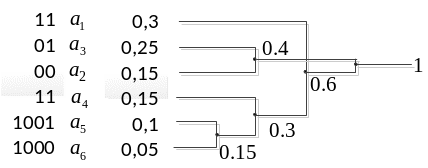
Коэффициент статистического сжатия: , где максимальная энтропия, - средняя длина кодовой комбинации.

Для обоих кодов ;

Шеннона-Фано , бит;

Хаффмана , бит;

- Шеннона-Фано

- Хаффмана

Коэффициент относительной эффективности: . Показывает степень использования статистической избыточности.

, .

- Шеннона-Фано

- Хаффмана