10.11 Дисконтированный срок окупаемости капитальных вложений.

Дисконтированный срок окупаемости – это такой период времени в течении которого инвестор накапливает денежные средства для инвестирования равные по своей величине первоначальным капитальным вложениям. Это такой момент времени начиная с которого ЧДД становится положительным. Значения дисконтированного срока окупаемости определяется графическим способом, с помощью графика ЧДД=F(t). Чем больше разница между продолжительностью фазы эксплуатации проекта и дисконтированным сроком окупаемости, тем величина ЧДД будет больше.

Методика расчета дисконтированного срока окупаемости.

Задаются продолжительностью жизненного цикла проекта, для этих значений рассчитывают ЧДД, наносят на график (плоскость) и строят график.

Дисконтированный срок окупаемости всегда больше простого срока окупаемости так как инвестор получает проценты из годовых чистых денежных поступлений. Чем величина процентов будет больше, тем разница будет больше.

Дисконтированный срок окупаемости капитальных вложений DPP (Discounted Payback Period)– это период времени от начала проекта до момента когда ЧДД становится положительным.

NPV

Т

годы

1 2 3 4 5

DPP=2,4года

Методика расчета DPP:

1.Задаем продолжительность жизненного цикла проекта 1 год. Рассчитываем NPV для одного года; задаем продолжительность проекта 2 года, рассчитываем NPV для двухлетнего проекта и т.д. до конца жизненного цикла.

2.Полученные значения наносим на график NPV=f(t).

3. По графику определяем DPP. Он всегда больше простого срока окупаемости DPP > PP, потому что при расчете DPP чистые денежные потоки уменьшаются на величину процентов, уплаченных инвестору., следовательно, срок возврата инвестиций откладывается на более поздние моменты времени. Надежность проекта оценивается по разности Т – DPP.

10.12 Отбор альтернативных проектов по критерию ЧДД и по показателю внутренней нормы доходности капитальных вложений.

Правило метода чистого дисконтированного дохода (ЧДД или NPV): если текущая оценка будущих чистых денежных потоков превышает текущую оценку инвестиционных затрат, то проект принимается. Чистый дисконтированный доход равен разнице текущей оценки отдачи и текущей оценки инвестиционных затрат.

Правило метода ЧДД гласит, что из двух альтернативных (взаимоисключающих) проектов с равными инвестиционными затратами выбирается тот, который обеспечивает наибольшее значение ЧДД. Например, для проектов А и Г при стоимости капитала 10% (ставка дисконтирования) ЧДД проекта А = = 79, а ЧДД проекта Г = 49,2. Метод ЧДД рекомендует выбор проекта А.

В сравнительном анализе альтернативных проектов критерий внутренней нормы прибыли ВНП можно использовать с известными оговорками. Так, если значение ВНП для проекта А больше, чем для проекта В, то проект А в определенном смысле может рассматриваться как более предпочтительный, поскольку допускает бoльшую гибкость в варьировании источниками финансирования инвестиций, цена которых может существенно различаться. Однако такое преимущество носит весьма условный характер. ВНП является относительным показателем, и на его основе невозможно сделать правильные выводы об альтернативных проектах с позиции их возможного вклада в увеличение капитала предприятия. Этот недостаток особенно четко проявляется, если проекты существенно различаются по величине денежных потоков.

Основным показателем эффективности проекта является его ЧДД. Вторичный показатель – ВНД.

Если имеется два или несколько проектов, из которых нужно выбрать только один, то процедура выбора проекта следующая: предположим, что имеется 2 проекта «А» и «Б». К_Б> К_А, а Д_Б> Д_А. Какой проект лучше?

Для того, чтобы выбрать лучший проект, нужно для каждого проекта построить графики функций NPV (i). Обычно эти графики выглядят следующим образом:

Б

NPV

А

А

Б

r_А

r_Б

Пересечение Фишера

i

Если i < i_кр, то лучше проект Б, поскольку у него NPV больше.

Если i > i_кр, то лучше проект А.

Если i = i_кр, то проекты А и Б эквивалентны.

В диапазоне i =0-i_кр два показателя вступают NPV и r вступают в противоречия: NPV_Б> NPV_А – лучше Б и r_Б< r_А – лучше А.

В диапазоне i > i_кр: NPV_Б> NPV_А – лучше А и r_Б>r_А – лучше А. В этом диапазоне противоречий этих показателей нет.

Объяснения кажущейся противоречивости показателей NPV и r в диапазоне от i =0 до i_кр:

В каждой ситуации следует ориентироваться либо на показатель NPV, либо на показатель ВНД.

1 ситуация: сравниваются 2 проекта с различной величиной капитальных вложений. В этом случае главным показателем является абсолютный прирост капитальных вложений в денежных единицах, т.е. следует ориентироваться на NPV.

2 ситуация: имеется фиксированная величина капитальных вложений и эти деньги нужно вложить в какую-то отрасль, проект или в ценные бумаги, в этом случае следует ориентироваться на относительную величину дохода, в данном случае это величина r, которая показывает минимальную величину процента, которую может получить инвестор с вложенного капитала.

На графике изображена 1 ситуация, капитальные вложения разные, доходы проекта максимально отличны, поэтому при любой процентной ставке выбор проекта осуществляется только по показателю NPV, т.е. наше решение исключительно зависит от цены капитала. (процентная ставка i как раз и есть цена капитала).

10.13 Реальная и номинальная ставка дисконта.

iном – номинальная ставка дисконтирования, то есть заранее известная или объявленная доходность капитала.

β- годовой темп инфляции.

i – реальная ставка дисконтирования, показывает реальную покупательскую способность денег в рыночной экономике.

Упрощенная связь этих показателей: i=iном-β.

Точная связь показателей: (1+iном)=(1+i)(1+β); .

Если Вгп>Врес, то предприятие получает доход. Если Вгп<Врес, то предприятие несет инфляционные убытки. Если Вгп=Врес, то инфляция обходит предприятие стороной и не влияет на показатели работы предприятия. Только в этом случае все равно, какую ставку дисконтирования использовать для расчета ЧДД.

(1)

(2),

Д* - прогноз годовых чистых денежных поступлений с учетом инфляции. В формуле (1) инфляция присутствует как в числителе, так и в знаменателе дроби, но она на величину ЧДД никакого влияния не оказывает.

;

Дt – годовые чистые денежные поступления без учета инфляции.

Формулы (1) и (2) дают один и тот же результат только в одном случае, когда темп инфляции на ресурсы, используемые предприятием и на готовую продукцию одинаковый. Если эти темпы отличаются, то следует использовать только формулу (1).

10.14 Учет инфляции при расчете ЧДД.

β – годовая прогнозируемая инфляция, доли единицы

i – реальная годовая процентная ставка. Показывает реальную покупательскую способность денег в рыночной экономике.

Упрощенная связь реальной и номинальной ставки i≈ i_ном- β.

Точная связь по формуле Фишера (1+ i_ном)=(1+i)(1+β),

i =(1 + i_ном)/(1 + β) –1

Существует 2 подхода к расчету ЧДД:

1. Без учета инфляции. Применяется редко, поскольку прогнозировать инфляционный доход или убытки не представляется возможным.

NPV = -NCF₀+∑^T_t=1 NCF_t / (1 + i)^t ≥0 (1)

2. С учетом инфляции.

NPV = -NCF₀+∑^T_t=1 NCF_t^⃰ / (1 + i_ном)^t ≥0 (2)

NCF_t – прогноз чистых денежных потоков в постоянных ценах без учета инфляции;

NCF_t^⃰ – прогноз чистых денежных потоков в постоянных ценах с учетом инфляции.

Возможны 3 варианта использования формулы:

1. Уровень инфляций низкий, процентные ставки по капиталу высокие, либо инфляция на входящие ресурсы и на готовую продукцию предприятия одинаковы.

2. Инфляция на готовую продукцию выше, чем на входящие ресурсы. Предприятие в этом случае получает прибыль от инфляции - инфляционный доход.

3. Инфляция на готовую продукцию меньше инфляции на ресурсы. Предприятие несет инфляционные убытки.

ГП

Сырье

Предприятие

Зарплата

Энергоресурсы

β_ГП

β_р

β_р – инфляция на ресурсы;

β_ГП – инфляция на готовую продукцию.

а) β_р ≈ β_ГП

б) β_ГП > β_р

в) β_ГП < β_р

В случае а) следует пользоваться формулой (1), поскольку формула (2) после несложных преобразований даст тот же результат.

NCF_t^⃰ /(1 + i_ном)^t = NCF_t / (1 + β)^t / ) = (1+i)^t(1+β)^t = NCF_t /(1 + i)^t

В случае б) и в) фактор инфляции игнорировать нельзя, поэтому при расчете NPV следует пользоваться только формулой (2), она показывает как доходы влияют на величину инфляции.

10.15 Учет инвестиционных рисков при расчете ЧДД.

Инвестиционные риски делят на 3 большие группы: риск снижения доходности проекта, риск прямых финансовых потерь, риск упущенных возможностей (выгоды). По своей природе риски делят на статистические и нестатистические. Статистические риски подчиняются законам математической статистики. нестатистические этим законам не соответствуют, напр., к ним относят системные риски. Статистич. риски д. уд-ть 3-м осн. треб-ям: 1) быть измеримыми; 2) быть однородными; 3) обладать св-вами нейтральности к единичному событию. Для учета стат. рисков исп-т 2 осн-е методики: а) учет риска по коэф-ту вариации чистых денежных поступлений v_Д = σ_Д / Д_ср * 100%, где σ_Д - среднеквадратическое отклонение чистых ден. поступлений, рассчит-ся по: σ_Д = ,

где х = 1- n – кол-во возможных исходов; Р_х – вероятность исхода х;

Д_ср = 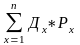. Чем больше коэф-т вариации чистых ден. поступлений, тем проект рискованнее.

б) по вер-ти обращения ЧДД в ноль: ЧДД_ср = ,

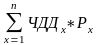σ_ЧДД = 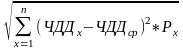, ЧДД_ср / σ_ЧДД = число стандартных отклонений, по которому в таблицах нормального распределения опред-ся вер-ть обращения ЧДД в ноль; 1 – вер-ть = вер-ть положительного ЧДД.

Если одно из трех правил для стат. рисков не выполняется, т.е. риски явл-ся нестатистическими, то в этом случае пользуются упрощенной методикой учета риска посредством введения поправки на риск – ставки дисконтирования: i_p = i_б + Δi_p, где i_p – ставка дисконта с учетом риска, i_б – безрисковая ставка, т.е. абсолютно надежная для инвестора альтернатива вложения капитала, Δi_p – поправка на риск или иначе премия инвестора (чем выше риск проекта, тем инвестор требует большей премии за риск). Метод введения поправки на риск считается менее строгим методом, чем статистический метод учета риска. Осн. недостаток м-да в том, что процесс дисконтирования чистых денежных поступлений приписывает чистым денежным поступлениям иную степень риска, чем изначально предполагал инвестор. ЧДД = - К + 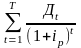≥ 0.

Третья методика позволяет учитывать риски через такие показатели, как операционный и финансовый рычаги. Операцион. рычаг показывает процентное изменение прибыли при процентном изменении выручки пр-тия. При увеличении объема продаж прибыль увеличивается более высокими темпами, чем выручка, и наоборот. Финансовый рычаг позволяет увеличить прибыль пр-тия посредством использования разности в доходности собственного и заемного капитала. i_а = i + K_з / К_а * (i – i_з). Если i > i_з, то возникает финансовый рычаг, т.е. за счет увеличения доли заемных ср-в можно увеличить дох-ть собств-го капитала (i_а). Однако при этом возникает риск невозврата заемных ср-в.

1