Cамостійна робота з теми «Многогранники» теоретичні відомості

Многогранник, дві грані якого – рівні n-кутники з відповідно паралельними сторонами, а всі інші n граней – паралелограми, називається n-кутною призмою. Її рівні n-кутники називаються основами призми, а паралелограми – бічними гранями, сторони основи – ребрами основи, інші ребра – бічними ребрами.

З означення призми впливає, що основи призми рівні, а також лежать в паралельних площинах. Бічні ребра паралельні й рівні. Поверхня призми складається з основ і бічної поверхні.

Висотою призми називається відстань між площинами її основ.

Відрізок, який сполучає дві вершини призми, що не належать одній грані, називається діагоналлю призми.

Пряма призма – призма, у якої бічні ребра перпендикулярні основам. Похила призма – призма, у якої бічні ребра не перпендикулярні основам.

Правильна призма – пряма призма, в основі якої лежить правильний многокутник. У такої призми всі бічні грані – рівні прямокутники.

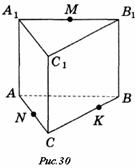
Основи призми: АВС; А₁В₁С₁

Бічні грані: АА₁В₁В; АА₁С₁С; СС₁В₁В

Бічні ребра: АА₁; ВВ₁; СС₁.

Вершини: А, В, С, А₁, В₁, С₁.

Діагональний переріз – це переріз, який проходить через два бічні ребра призми, що не належать одній грані.

Паралелепіпедом називається призма, в основі якої лежить паралелограм.

Прямий паралелепіпед – паралелепіпед, у якого бічні ребра перпендикулярні до площин основ.Чотири бічні грані – прямокутники, а дві основи– паралелограми.

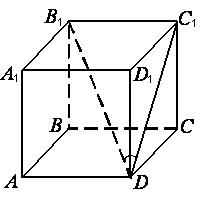
Похилий паралелепіпед – паралелепіпед, у якого бічні ребра не перпендикулярні площинам основ. Всі шість граней – паралелограми.

Прямокутний паралелепіпед – прямий паралелепіпед, у якого основною є прямокутник. Три ребра прямокутного паралелепіпеда, що виходять з однієї вершини, називаються його вимірами.

Властивості прямокутного паралелепіпеда

1. У прямокутного паралелепіпеда всі грані – прямокутники.

2. У прямокутного паралелепіпеда квадрат будь-якої діагоналі дорівнює сумі квадратів всіх його вимірів.

d² = a² + b² + с²

У прямокутному паралелепіпеді всі діагоналі рівні.

3. V = abc, де a, b, c – три виміри прямокутного паралелепіпеда.

Кубом називається прямокутний паралелепіпед, у якого всі ребра рівні. У куба всі грані – квадрати.

Повна поверхня призми дорівнює сумі бічної поверхні і площ основ:

S_пов. = S_бок + 2S_осн.

S_бок = P_осн. · H

, де H – висота, P_осн – периметр основи.

V = abc

– об’єм прямокутного паралелепіпеда.

V_призми = S_осн. · H

– об’єм призми.

n– кутною пірамідою називається многогранник, одна грань якого – довільний n– кутник, всі інші n граней – трикутники, що мають спільну вершину.

Спільну вершину трикутних граней називають вершиною піраміди, протилежну їй грань – основою, а всі інші грані – бічними гранями піраміди.

Відрізки, що сполучають вершину піраміди з вершинами основи, називають бічними ребрами.

Перпендикуляр, опущений з вершини піраміди на площину її основи, називають висотою піраміди.

Висотою також називають і довжину цього перпендикуляра.

S

ABCD– чотирикутна піраміда

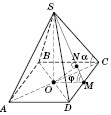
Вершина: S

Висота піраміди: SO

Основа піраміди: ABCD

Бічні ребра: SA,SB,SC,SD

Ребра основи:AB,BC,CD,AD

Апофема: SM.

Апофемою правильної піраміди називається висота бічної грані. Віссю правильної піраміди називається пряма, яка містить висоту піраміди. Піраміда називається правильною, якщо її основа є правильний многокутник, а основа висоти співпадає з центром цього многокутника.