8. Распределения нагрузки по направлениям. Понятие о коэффициентах тяготения
При распр-и нагрузок м/у станциями необх-мо рассматривать раздельно входящ и исходящ нагрузку. Величины потоков телеф нагрузки м/у станциями определяются полностью взаимной заинтересованностью абонентов в телеф связи (телеф тяготением). При сложении и разделении потоков Тел Нагр необходимо использовать средние нагрузки, а не расчетные нагрузки. Относительная колеблемость нагрузки направления зависит от Yсредн.. При распределении исходной нагрузки i – АТС по направлениям необходимо учитывать, что нагрузка на вых ступеней групп искания отличается от нагрузок на входах.
Нагрузка на выходе
.
Iги
– 1 –я ступень группового искания, t
– длит-ть занятия входа и выхода нагрузки
соответственно. Как правило,
на величину
.
Обычно при
распределении нагрузки на выходе станции
.
- 5-7%, (межгород),
- 1-2% (узел спецсвязи)
Пропорциональное распределение нагрузки (самый простой способ) – зависит от числа абонентов АТС.
Для распределения нагрузок на сети обычно строится матрица распредел нагрузок. Всего в сети m станций: .
-
нагрузка, исходящая
от i
станции. ЧНН
для всех направлений i
и j
совпадает, тогда это условие справедливо.
Входящая нагрузка
.
Коэффициент
распределения нагрузки:
,
условие нормировки:
,
.
Реальные стационарные потоки далеки от нагрузки. Поэтому сначала, когда бурно стали развиваться сети и предложили коэффициенты телефонного тяготения, которые зависят от абонентов сети, от расстояния между АТС.
f
ij
– коэффициент
межстанционного тяготения
– отношение фактического значения
интенсивности нагрузки от i
АТС к j
АТС к тому значению интенсивности
нагрузки, к-е было бы м-у этими станциями
при равномерном тяготении.
Позволили достаточно хорошо рассчитывать телефонную сеть. Но стоит модернизировать станцию, как все коэффициенты f рушатся.
Н
ормированные
коэф-ты тяготения (более стабильны):
,
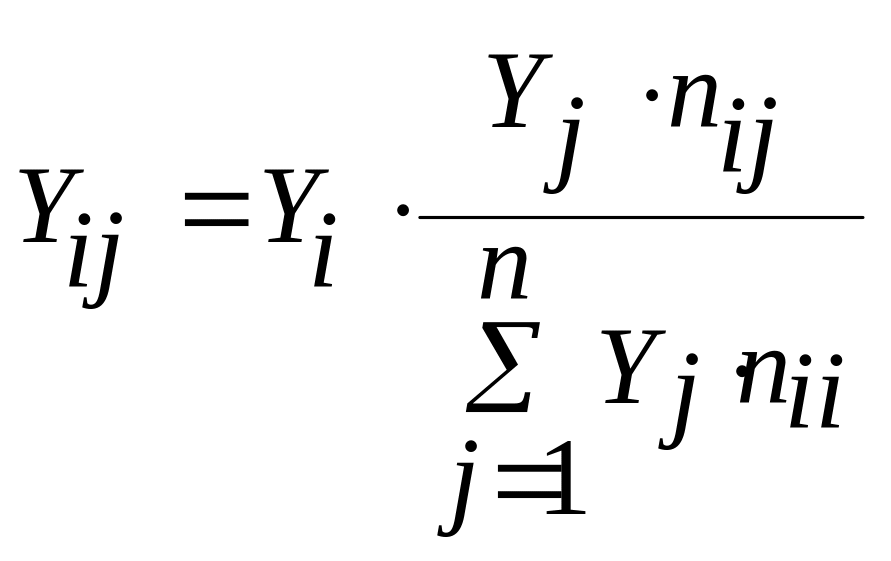
9. ОБСЛУЖИВАНИЕ ПРОСТЕЙШЕГО ПОТОКА ВЫЗОВОВ ПОЛНОДОСТУПНЫМ ПУЧКОМ ЛИНИЙ С ПОТЕРЯМИ. Определим математическую модель:
1.КС однозвенная, на выходы кот. включен ПД пучок емкостью V линий. Это означает, что любой вход КС м.б. подключен к любой из V линий, причем подключение входа к выходу осущ-ся в одной точке.
2.
На входы КС поступает простейший поток
вызовов с параметром потока λ.
- функция распределения. Закон распределения
.
Будем считать, что длительность
обслуживания вызовов (длительность
занятия одной линии) – это случайная
величина, распределенная по показательному
закону с параметром β:
.
Параметр β можно рассматривать как
плотность потока освобождения. Средняя
длительность занятия
.
Вероятность освобождения 1-й линии
1-[1 - β·t
+ 0(t)]
= β·t
+ 0(t)
3.В качестве дисциплины обслуживания примем обслуживание с явными потерями, т.е. при занятии всех линий поступивший вызов получает отказ соединения и в систему не возвращается. Потерянный вызов не оказывает влияния на систему.
M | M | V < ∞ М - Марковский простейший поток на входе
М – Экспоненциальное время обслуживания
V – Очереди в системе нет (конечное число приборов)
Если говорить о состоянии системы, когда занято i линий из V и нам безразлично, какие это i линий, в этом случае будем говорить о макросостояниях. Микросостояния – конкретно о 1й, 2й, 10й линии.
Постановка задачи Для данной мат модели требуется найти вероятность занятия Pi(t) любых i линий из V в фиксированный момент времени. Pi(t) - ?
Диаграмма переходов. Пусть Х0 – состояние системы, которое соответствует тому, что все линии свободны. Х1 – поступил один вызов, занята 1 линия.
λ- параметр входящего потока; β – параметр потока освобождения
ПЕРВАЯ ФОРМУЛА ЭРЛАНГА.
1. Первая формула Эрланга
-
используется интенсивность поступающей
нагрузки.
Если V→∞, то распределение Эрланга переходит в распределение Пуассона:
1-я ф-ла Эрланга справедлива при любом распределении длительности обслуживания, лишь бы поступивший на вход КС поток был простейшим.