21. Коммутационные системы с обходными направлением.

Принцип построения сети с обходными направлениями можно пояснить на следующем простом примере. Рассмотрим три АТС_i, АТС_j, , АТС_k, (рис).

Введем следующие обозначения: У_ij, У_ik, У_ij - интенсивности нагрузки, поступающей от АТС_i к АТС_j, от АТС_i к АТС_k, от АТС_k к АТС_j; с_ij , с_ik , с_kj - капитальные затраты на 1 канал – км. линейных сооружений направлений ij , ik, kj соответственно; l_ij , l_ik , l_kj - длина соединительной линии на соответствующем направлении; с_вхi , с_вхj , с_вхk - капитальные затраты на один вход коммутационного оборудования на АТС i, j и k.

Капитальные затраты на одну линию в направлении ij обозначим . Задача состоит в таком распределении нагрузки Y_ij между направлениями ij и ikj при котором обеспечивались бы минимальные капитальные затраты на линейные сооружения и станционное оборудование при заданном качестве обслуживания.

Если станция АТС_i имеет возможность набора обходного направления, то нагрузка Y_ij в начале предлагается линиям прямого направления ij. Нагрузка, не обслуженная линиями прямого направления, автоматически передается на направление, состоящее из двух участков: ik и kj. Эту нагрузку называют избыточной. Направление, на которое поступает избыточная нагрузка, называют обходным.

Расчет сети с обходными направлениями в общем случае сводится к решению двух задач:

0. Определению такого числа линий на прямых направлениях, чтобы суммарные затраты на построение сети были минимальными;

1. Расчету такого числа линий на обходных направлениях, чтобы обеспечивалось заданное качество обслуживания потоков вызовов.

Основная трудность решения поставленных задач заключается в расчете числа линий в обходных направлениях. Дело в том, что поток вызовов, создающий избыточную нагрузку, не является простейшим, а имеет ярко выраженный "пиковый" характер. Распределение вероятностей избыточного потока вызовов описывается не распределением Пуассона, а отрицательным биномиальным распределением. При прочих равных условиях для обслуживания избыточного потока необходимо иметь больше линий, чем для обслуживания простейшего потока.

Оптимальное число линий в прямом направлении зависит от:

- интенсивности нагрузки, поступающей на прямое направление ij Y_ij;

- отношения затрат на одну линию в прямом направлении к затратам на одну линию в обходном направлении ;

- величины потерь, с которыми рассчитывается количество линий в обходном направлении Р_обх.

22. Определение оптимального числа линий в прямом направлении для кс с обходными направлениями.

Расчет сети с обходными направлениями в общем случае сводится к решению двух задач:

0. определению такого числа линий на прямых направлениях, чтобы суммарные затраты на построение сети были минимальными;

1. расчету такого числа линий на обходных направлениях, чтобы обеспечивалось заданное качество обслуживания потоков вызовов.

Введем следующие обозначения: У_ij, У_ik, У_kj - интенсивности нагрузки, поступающей от АТС_i к АТС_j, от АТС_i к АТС_k, от АТС_k к АТС_j; с_ij , с_ik , с_kj - затраты на 1 каналокилометр в направлении ij , ik, kj соответственно; l_ij , l_ik , l_kj - длина соединительной линии на соответствующем направлении; с_вхi , с_вхj , с_вхk - капитальные затраты на один вход коммутационного оборудования на АТС i, j и k.

Капитальные затраты на одну линию в направлении ij обозначим . Задача состоит в таком распределении нагрузки Y_ij между направлениями ij и ikj при котором обеспечивались бы минимальные капитальные затраты на линейные сооружения и станционное оборудование при заданном качестве обслуживания.

Если число линий м-у i и j =0,узловая схема; если = Vij полносвязная; все, что м-у ними – с обходными направлениями, V*ij – оптимальная.

Оптимальное число линий в прямом направлении зависит от:

0. интенсивности нагрузки, поступающей на прямое направление ij Y_ij;

1. отношения затрат на одну линию в прямом направлении к затратам на одну линию в обходном направлении ;

2. величины потерь, с которыми рассчитывается количество линий в обходном направлении Р_обх.

Число линий в прямом направлении будем считать оптимальным, если выполняются следующие условия:

0. экономия, от уменьшения числа линий в прямом направлении на одну от оптимального, не превышает затрат, на организацию дополнительного числа линий в обходном направлении ;

1. затраты на организацию дополнительной линии в прямом направлении больше экономии от соответствующего уменьшения числа линий на обходном направлении .

2. Уменьшение числа линий на соответствующих участках обходн направления, если в прямом направлении происходит увеличение на 1. ,

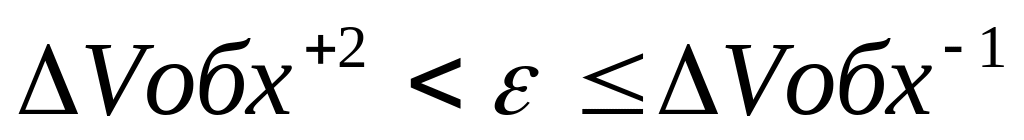
При полнодоступном не блокируемом включении линий МККТТ рекомендует (Рекомендация Е.522) использовать следующее условие оптимальности: .

где - первая формула Эрланга; M - увеличение пропускной способности пучка линий обходного направления при добавлении к этому пучку одной линии.

Если зафиксировать и P_обх = const, то ,где a, b – табулированные коэффициенты.