Примеры выполнения курсовой работы

Пример 1. Несвободная система с двумя степенями свободы. Дано: Полый цилиндр 2 массой m₂ (рис. 6.4) скользит по основанию 1 массой m₁, способному вращаться вокруг неподвижного цилиндрического шарнира О. Основание удерживается спиральной пружиной с крутильной жесткостью C_. В начальном положении механизм находится в состоянии статического равновесия и пружина деформирована. Введем неподвижную систему координат OXYZ так, чтобы ось OX была горизонтальна, и связанную с основанием систему координат OX₁Y₁Z₁, ее ось OX₁ параллельна оси цилиндра и направляющим основания, по которым скользит цилиндр. Центр масс основания O₁ в системе координат OX₁Y₁Z₁ имеет координаты x_1O и y_1O. Начальное положение O_н центра масс цилиндра O₂ определяется координатами x_2O и y_2O точки O_н в системе координат OX₁Y₁Z₁.

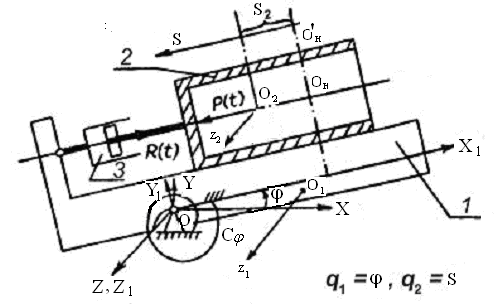
Рис. 6.4

В начальный момент времени к внутренней поверхности дна цилиндра прикладывается нагрузка , определяемая по формуле (6.1). При этом цилиндр начинает двигаться по основанию, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией тормозного устройства 3, приложенной к внешней поверхности дна цилиндра , определяемой по формуле (6.2).

Коэффициент трения скольжения при движении цилиндра по основанию f = 0,12. Моменты инерции основания и цилиндра относительно осей O₁z₁ и O₂z₂ равны J₁ и J₂ соответственно. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.

Указание. В качестве обобщенных координат выбрать угол поворота  основания, отсчитанный от горизонтали (в начальный момент  = ₀), и координату  S центра масс цилиндра  на направляющей основания, отсчитанную от его начального положения. Исходные данные:

кг,  кг, 

кг∙м²,   кг∙м²,

м, м,

м, м,

Н∙м/рад , .

Решение. Система имеет две степени свободы k = s , в качестве обобщенных координат выбираем:

1) угол поворота   основания  вместе с цилиндром , отсчитанный от горизонтали (в начальный момент  = ₀), q₁=j;

2) координату  S движения центра масс цилиндра 2 на направляющей основания 1, отсчитанную от его начального положения, q₂=S.

Таким образом, обобщенные координаты: q₁=j, q₂=S, обобщенные скорости: .

Запишем уравнения Лагранжа второго рода

.

Кинетическая энергия рассматриваемой механической системы относительно неподвижной системы отсчета: Т=Т₁+Т₂. Представим ее как функцию времени t, обобщенных координат q₁=j, q₂=S и обобщенных скоростей , а именно:

T = T (q₁=j, q₂=S, , t).

Кинетическая энергия основания, совершающего вращательное движение относительно оси OZ,

Кинетическая энергия цилиндра, совершающего плоско-параллельное движение относительно неподвижной системы отсчета,

Формулы преобразования координат и поворотная матрица относительно оси OZ в соответствии с формулами (3.18) и (3.19) имеют следующий вид:

– для центра масс основания

– для центра масс цилиндра

Матрица скоростей:

После приведения подобных членов относительно обобщенных скоростей, получаем T= T₁+T₂,

Уравнения Лагранжа второго рода для данной системы имеют следующий вид:

– для q₁

– для q₂

Вычислим производные от кинетической энергии системы:

– для q₁ =φ ,

окончательно

где

Для q₂ =S ,

.

В левой части уравнений Лагранжа, как правило, оставляют слагаемые со вторыми производными от обобщенных координат. Все остальные переносятся в правую часть. Таким образом, обозначив слагаемое в последнем выражении как - окончательно получаем уравнение Лагранжа второго рода

.

Обобщенные силы для механических систем с числом степеней свободы i = s = 2 , , отвечающие выбранным обобщенным координатам, целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации не зависят друг от друга. Системе всегда можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае из (2.15) получаем:

. (6.6)

Для определения обобщенной силы дадим системе такое приращение, что 1) , и найдем виртуальную работу от всех заданных активных сил:

,

, ,

Сравнивая множитель (в квадратных скобках) в выражении виртуальной работы перед вариацией  с формулой (6.6), получаем выражение для первой обобщенной силы

Определяя , будем полагать, что S  0, а для угла  поворота цилиндра 2, будем считать  =0 ( =const), т.е.

2) S  0,  =0  ( = const); .

Сравнивая множитель (в квадратных скобках) в выражении полученной виртуальной работы перед вариацией S с формулой (6.6), получаем выражение для второй обобщенной силы

.

Составим дифференциальные уравнения в виде матриц

.

Для

Для

окончательно

1)

2) ,

где , если , , если ,

т.е. ;

;

.

Пример 2. Несвободная система с тремя степенями свободы. Дано. Рекомендуемые значения физических величин (рис. 6.5): m₁ = 3 700 кг – масса тела; = 10 300 кг·м² – момент инерции относительно оси О₁z₁; l₁ = 3,8 м – расстояние от точки С до точки К; координаты центра масс тела О₁ в системе координат СX₁Y₁Z₁: х₁₀ = 3,8 м , y₁₀ = 0,8 м, y₂₀ = 1,0 м – расстояние от линии действия силы до оси СХ₁ ; С₁ = 2,0·10⁶ Н/м – жесткость пружины КМ; С₂ = 2,0·10⁷ Н/м – жесткость пружины CD ; С₃ = 2,0·10⁷ Н/м – жесткость пружины СЕ; С_ = 2,0·10⁶ Нм/рад – жесткость спиральной пружины; ₀ = 6°, 30° – начальный угол возвышения основания.

Рис. 6.5

За обобщённые координаты приняты следующие параметры:

q₁ = x_C , q₂ = y_C , q₃ = . q₁ = x_C – перемещение шарнира С по горизонтальной оси, отсчитанное от положения статического равновесия пружины CD; q₂ = y_C – перемещение шарнира С вдоль вертикальной оси, отсчитанное от положения статического равновесия пружины CЕ; q₃ =  – угол поворота тела, отсчитанный от горизонтали СХ₁.

Кинетическая энергия рассматриваемого тела, совершающего плоскопараллельное движение относительно неподвижной системы отсчета и связанной с ней системой координат XOYZ:

.

Формулы преобразования координат от СX₁Y₁Z₁ к XOYZ и поворотная матрица относительно оси СZ в соответствии с формулами (3.18) и (3.19) для центра масс тела 1 имеют следующий вид:

Матрица скоростей:

.

Квадрат абсолютной скорости центра масс тела в обобщённых координатах:

Кинетическую энергию тела представим как функцию времени t, обобщенных координат q₁ = x_C , q₂ = y_C , q₃ =  и обобщенных скоростей :

T = T (q₁=x_C, q₂ = y_C , q₃ = , .

Уравнения Лагранжа второго рода для данной системы имеют вид:

– для ;

– для ;

– для .

Частные производные по обобщённым координатам:

;

Частные производные по обобщённым скоростям:

Полные производные по времени:

Запишем окончательно левые части уравнений Лагранжа второго рода, оставив только слагаемые со вторыми производными от обобщенных координат. Все остальные слагаемые перенесем в правую часть уравнения, обозначив их как :

–

где

–

где

–

, где .

Для нахождения обобщенных сил рассмотрим приложенные к системе силы. Определим первоначальные сжатия пружин КМ и СЕ в положении статического равновесия.

Уравнение равенства моментов при t=0 относительно оси CZ₁

,

где  момент силы тяжести в момент времени t=0; – момент силы упругости пружины КМ. Отсюда

 первоначальное сжатие пружины КМ.

Уравнение равенства сил по оси OY

,

где – сила упругости пружины КМ; – сила упругости пружины СЕ, отсюда

 первоначальное сжатие пружины СЕ

Силы, действующие на тело в текущий момент времени t:

– сила тяжести;

– переменная нагрузка, прикладываемая к телу; где Р₁  =  2,37·10⁶  Н – максимальная нагрузка; а₁ = 6,68·10¹⁰ Н/с² – коэффициент; t₁ = 0,005 с – временной параметр;

– сила упругости пружины КМ,

где – координата точки К в момент времени t ; – координата точки К в начальный момент времени; – константа;

– сила упругости пружины CD ; –

сила упругости пружины СЕ.

Моменты, действующие на тело, относительно оси CZ₁ :

– момент силы тяжести;

– момент переменной нагрузки;

– момент силы упругости пружины КМ;

– момент спиральной пружины.

Виртуальная работа согласно (2.15)

. (6.7)

Так как обобщённые координаты – независимые друг от друга параметры, то и их вариации тоже независимы. Поэтому, используя принцип замораживания, находим виртуальные работы, соответствующие виртуальным перемещениям поочередно:

1) ,

;

2) , (6.8)

;

3) ,

.

Сравнивая множители в (6.7) перед вариациями обобщённых координат и в формуле (6.8), находим обобщённые силы, соответствующие обобщённым координатам:

;

;

Окончательный вид уравнений Лагранжа второго рода или дифференциальные уравнения движения рассматриваемой системы в обобщенных координатах:

–

,

где

–

где

–

где ,

или в матричной форме ,

где – инерционная матрица, , если , , если ,

,

=

– матрица-столбец обобщенных сил;

– матрица-стол-бец слагаемых, перенесенных из левых частей уравнений Лагранжа, не содержащих обобщенных ускорений.

Решение системы уравнений Лагранжа второго рода, описывающих движение указанной механической системы (рис. 6.5), на интервале времени от t = 0 до t = 0,01 с выполнено в системе Mathcad 11. Распечатка результатов расчёта в системе Mathcad 11 для начального угла ₀ = 30° приведена на рис. 6.6, а для начального угла ₀ = 6° на рис. 6.7.

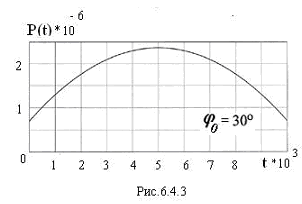
Рис. 6.6

Рис. 6.6. Окончание

Пример 3. Несвободная система с тремя степенями свободы. Дано. Полый цилиндр 2 массой m₂ (рис. 6.8) скользит по основанию 1 массой m₁, опирающемуся на цилиндрический шарнир О и поддерживаемому вертикальной пружиной КМ. Жесткость пружины C₁, длина недеформированной пружины l₂, расстояние от шарнира О до точки К опоры пружины l₁. Коэффициент трения цилиндра об основание f = 0,12. K шарниру C прикреплена горизонтальная пружина CD жесткостью C₂. В начальном положении пружина CD не деформирована, а пружина КМ поддерживает систему в положении статического равновесия.

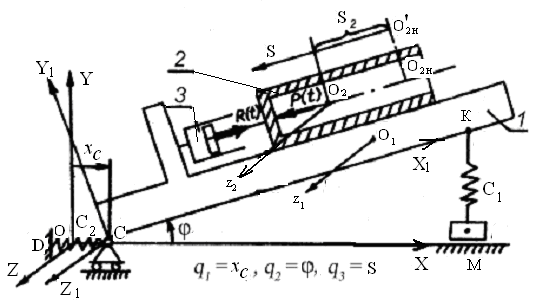
Рис.6.8

Введем неподвижную систему координат OXYZ, ось OX которой горизонтальна, и связанную с основанием систему координат OX₁Y₁Z₁, ее ось OX₁ параллельна направляющей основания, по которой скользит цилиндр. Положение центра масс O₁ основания задается координатами x_1O и y_1O точки O₁ в системе координат OX₁Y₁Z₁, причем y_1O = 0,6 м. Начальное положение цилиндра на основании определяется начальными значениями координат x_2O и y_2O точки O₂ в системе координат OX₁Y₁Z₁. Точка O_н совпадает с начальными положением центра масс цилиндра O₂.

В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P(t), определяемая по зависимости (6.1). При этом цилиндр 2 начинает скользить по основанию 1, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией R(t) тормозного устройства 3, приложенной к внешней поверхности дна цилиндра. Величина реакции определяется по формуле (6.2). Моменты инерции основания и цилиндра относительно осей O₁z₁ и O₂z₂ равны J₁ и J₂ соответственно.

Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.

Указание. В качестве обобщенных координат выбрать: 1) перемещение точки C по горизонтальной оси , отсчитанное от положения статического равновесия пружины CD; 2) угол поворота  основания , отсчитанный от горизонтали, и 3) перемещение  S центра масс  цилиндра 2 по направляющей основания 1 , отсчитанное от его начального положения O_н. Начальное значение  = ₀. Длину недеформированной пружины  l₂ определить из условия статического равновесия системы в начальный момент времени. Рекомендуемые значения величин приведены в табл. 6.3.

Исходные данные: m₁ – масса основания; m₂ – масса цилиндра. Число степеней свободы: i =s = 3. За обобщенные координаты приняты следующие параметры: ; ; . Обобщенные скорости: ; ; . В рассматриваемую механическую систему входят: основание 1 и цилиндр 2, совершающие плоскопараллельное движение относительно неподвижной системы координат OXYZ,

; ;

; , i=1,2,

где

Координаты центра массы основания в матричной форме:

(1), или

, где , т.е.

Скорости центра массы основания в матричной форме:

, или

;

;

Кинетическая энергия основания в функции обобщенных координат и обобщенных скоростей:

Координаты центра массы цилиндра в матричной форме:

.

Скорости центра массы цилиндра 2 в матричной форме:

, или

;

.

их квадраты:

Кинетическая энергия цилиндра в функции обобщенных координат и обобщенных скоростей:

Кинетическая энергия системы

Уравнения Лагранжа второго рода для данной системы:

Для :

;

окончательно левая часть уравнения по

;

Для :

окончательно левая часть уравнения по

;

Для :

окончательно

Перепишем уравнения Лагранжа второго рода, оставив в левой части только слагаемые со вторыми производными от обобщенных координат. Все остальные слагаемые перенесем в правую часть уравнения, обозначив их как

Уравнения Лагранжа второго рода в матричной форме:

,

где – инерционная матрица, , если , , если ,

или ,

инерционные коэффициенты:

;

;

;

;

.

Виртуальная работа сил, действующих на рассматриваемую систему:

;

.

Так как обобщённые координаты  независимые друг от друга параметры, то и их вариации тоже независимы. Поэтому, используя принцип замораживания, находим виртуальные работы, соответствующие виртуальным перемещениям поочередно:

1)  ,

;

2) ,

3)  ,

.

Сравнивая множители в выражениях виртуальных работ перед вариациями соответствующих обобщённых координат и в формуле (6.7), находим обобщённые силы, соответствующие обобщённым координатам:

;

.